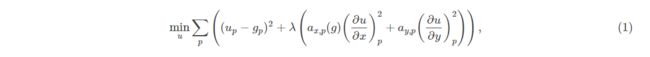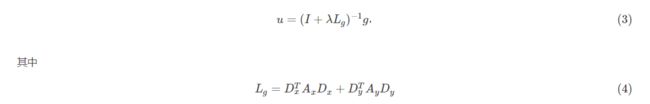Matlab&Python-WLS加权最小二乘滤波
最近看了论文Non-local Image Dehazing基于雾线的去雾算法。
其中算法的滤波用的是weighted least square(WLS)算法,论文全称《Edge-Preserving Decompositions for Multi-Scale Tone and Detail Manipulation》,作者Z. Farbman等,发表在ACM SIGGRAPH 2007。
保边滤波器可以是两个矛盾的目标的结合体。对于一副输入图像g(N*M),我们目标图像u一方面我们希望其尽可能近似,与此同时除了在一些边缘梯度变化比较大的地方外应该越平滑越好。数学模型为:
下标代表像素点空间位置,其中p表示像素的位置,ax和ay控制着不同位置上的平滑程度。
目标函数第一项代表输入图像和输出图像越相似越好,第二项是正则项,通过最小化的偏导,使得输出图像越平滑越好。平滑项的权重分别是和,依赖于输入图像,当输入图像的边缘梯度变化比较大的时候,我们希望其约束小一些,以保留图像的结构信息;当图像的边缘梯度变化很小的时候,这些细节信息我们认为其不重要,约束自然可以大一些,lambda是正则项参数,平衡两者比重,越大图像也就越平滑。
上式写成矩阵就是:
其中,Ax,Ay为以ax,ay为对角元素的对角矩阵,Dx,Dy为前向差分矩阵,和是后向差分算子,要使得(2)式去的最小值,u需满足如下:
Lg为五点空间异构Laplacian矩阵。
论文中的去的平滑权重系数为:
输入图像亮度通道的log值(其实直接用原始图像也是可行的),可以看出当的梯度比较大时,会随着变小,否则反之。权重的这样设计是很合理的,可以保留较大的边缘,平滑不必要的细节。 其中 l 表示log, ε一般取0.0001。
原作者在项目主页中公布了源码:
稀疏矩阵A就是公式(3)中的I+λLg。这段程序和前面的推导不同之处在于平滑权重先乘以了−λ,但是最中的结果是一致的:对角线上用1去减,其实就是加;对于其他四个对角线,我们推导的结果是带有负号的平滑权重,然后乘以λ,其实就等价于直接乘以−λ。
wlsFilter.m
function OUT = wlsFilter(IN, lambda, alpha, L)
%WLSFILTER Edge-preserving smoothing based on the weighted least squares(WLS)
% optimization framework, as described in Farbman, Fattal, Lischinski, and
% Szeliski, "Edge-Preserving Decompositions for Multi-Scale Tone and Detail
% Manipulation", ACM Transactions on Graphics, 27(3), August 2008.
%
% Given an input image IN, we seek a new image OUT, which, on the one hand,
% is as close as possible to IN, and, at the same time, is as smooth as
% possible everywhere, except across significant gradients in L.
%
%
% Input arguments:
% ----------------
% IN Input image (2-D, double, N-by-M matrix).
%
% lambda Balances between the data term and the smoothness
% term. Increasing lambda will produce smoother images.
% Default value is 1.0
%
% alpha Gives a degree of control over the affinities by non-
% lineary scaling the gradients. Increasing alpha will
% result in sharper preserved edges. Default value: 1.2
%
% L Source image for the affinity matrix. Same dimensions
% as the input image IN. Default: log(IN)
%
%
% Example
% -------
% RGB = imread('peppers.png');
% I = double(rgb2gray(RGB));
% I = I./max(I(:));
% res = wlsFilter(I, 0.5);
% figure, imshow(I), figure, imshow(res)
% res = wlsFilter(I, 2, 2);
% figure, imshow(res)
if(~exist('L', 'var')) %参数不存在,选取的默认值
L = log(IN+eps);
end
if(~exist('alpha', 'var'))
alpha = 1.2;
end
if(~exist('lambda', 'var'))
lambda = 1;
end
smallNum = 0.0001;
[r,c] = size(IN);
k = r*c;
% Compute affinities between adjacent pixels based on gradients of L
dy = diff(L, 1, 1); %对L矩阵的第一维度上做差分,也就是下面的行减去上面的行,得到(N-1)xM维的矩阵
dy = -lambda./(abs(dy).^alpha + smallNum);
dy = padarray(dy, [1 0], 'post');%在最后一行的后面补上一行0
dy = dy(:);%按列生成向量,就是Ay对角线上的元素构成的矩阵
dx = diff(L, 1, 2); %对L矩阵的第二维度做差分,也就是右边的列减去左边的列,得到Nx(M-1)的矩阵
dx = -lambda./(abs(dx).^alpha + smallNum);
dx = padarray(dx, [0 1], 'post');%在最后一列的后面添加一列0
dx = dx(:);%按列生成向量,对应上面Ax的对角线元素
% Construct a five-point spatially inhomogeneous Laplacian matrix
B(:,1) = dx;
B(:,2) = dy;
d = [-r,-1];
A = spdiags(B,d,k,k);%把dx放在-r对应的对角线上,把dy放在-1对应的对角线上
e = dx;
w = padarray(dx, r, 'pre'); w = w(1:end-r);
s = dy;
n = padarray(dy, 1, 'pre'); n = n(1:end-1);
D = 1-(e+w+s+n);
A = A + A' + spdiags(D, 0, k, k);%A只有五个对角线上有非0元素
% Solve
OUT = A\IN(:);
OUT = reshape(OUT, r, c);
demo_wlsFilter.m
img = imread('C:\Users\x\Desktop\15.jpg');
IN = double(img);
OUT = IN;
%OUT = wlsFilter(IN, 0.5);
if length(size(img))>2
for i=1:3
IN(:,:,i) = IN(:,:,i)/max(IN(:));
OUT(:,:,i) = wlsFilter(IN(:,:,i),0.35);
end
end
figure('Position',[50,50, size(IN,2)*2 , size(IN,1)]);
subplot(1,3,1); imshow(IN);title('input')
subplot(1,3,2); imshow(OUT); title('output')
imwrite(OUT,['C:\Users\x\Desktop\', int2str(16),'.jpg']);
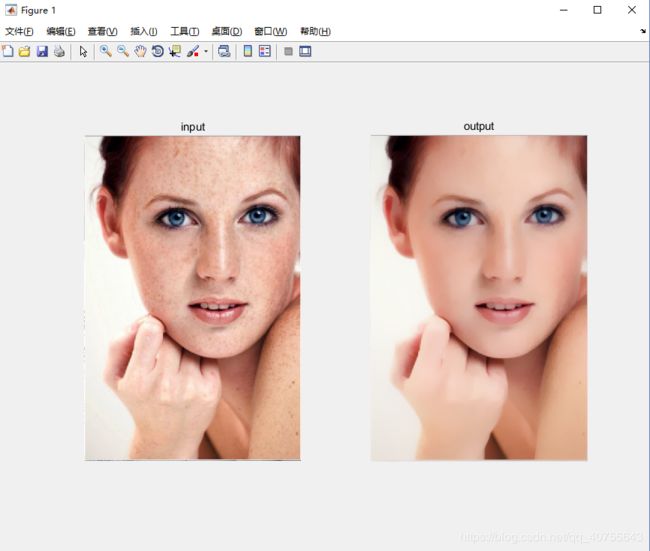
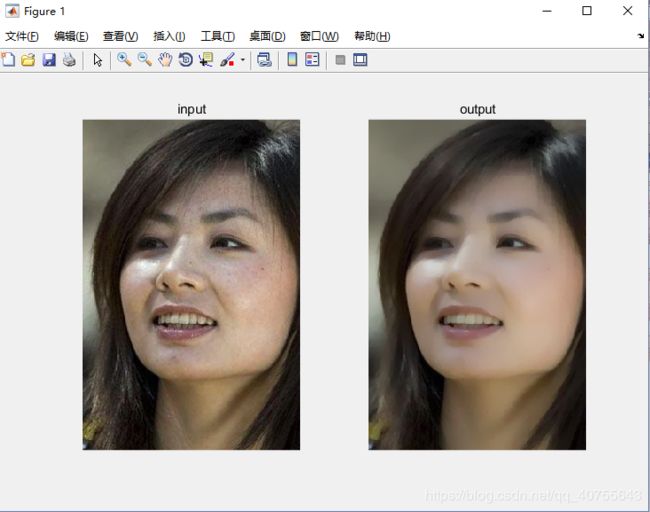
平滑结果:
Python实现
由于numpy的矩阵很容易溢出出现MemoryError,而A的大小很容易超过10万行&列,所以图片必须压缩。测试代码用的是(128x128)大小的图片。
还有一点就是python的spdiags与matlab的参数是不一样的。spdiags(B, diags, k, k)这里的B要用matlab的B参数的转置。另外python没有\除,所以矩阵a必须先求逆矩阵,由于矩阵是16384x16384大小,所以代码要跑3分钟。。。
import numpy as np
import cv2
#import math
from scipy.sparse import spdiags
def wlsFilter(img, Lambda, alpha=1.2, eps=0.0001):
L = np.log(img+0.0001)
row, cols = img.shape[:2]
k = row * cols
#对L矩阵的第一维度上做差分,也就是下面的行减去上面的行,得到(N-1)xM维的矩阵
dy = np.diff(L, 1, 0)
dy = -Lambda/(np.power(np.abs(dy),alpha)+eps)
#在最后一行的后面补上一行0
dy = np.pad(dy, ((0,1),(0,0)), 'constant')
#按列生成向量,对应上面Ay的对角线元素
dy = dy.T
dy = dy.reshape(-1,1)
#对L矩阵的第二维度上做差分,也就是右边的列减去左边的列,得到Nx(M-1)的矩阵
dx = np.diff(L, 1, 1)
dx = -Lambda/(np.power(np.abs(dx),alpha)+eps)
#在最后一列的后面补上一行0
dx = np.pad(dx, ((0,0),(0,1)), 'constant')
#按列生成向量,对应上面Ay的对角线元素
dx = dx.T
dx = dy.reshape(-1,1)
#构造五点空间非齐次拉普拉斯矩阵
B = np.hstack((dx,dy))
B = B.T
diags = np.array([-row, -1])
#把dx放在-row对应的对角线上,把dy放在-1对应的对角线上
A = spdiags(B, diags, k, k).toarray()
e = dx
w = np.pad(dx, ((row,0),(0,0)), 'constant')
w = w[0:-row]
s = dy
n = np.pad(dy, ((1,0),(0,0)), 'constant')
n = n[0:-1]
D = 1-(e+w+s+n)
D = D.T
#A只有五个对角线上有非0元素
diags1 = np.array([0])
A = A + np.array(A).T + spdiags(D, diags1, k, k).toarray()
im = np.array(img)
p,q = im.shape[:2]
g = p*q
im = np.reshape(im,(g,1))
a = np.linalg.inv(A)
out = np.dot(a,im)
out = np.reshape(out,(row, cols))
return out
img = cv2.imread(r'C:\Users\x\Desktop\k2.jpg', cv2.IMREAD_ANYCOLOR)
m = np.double(img)
b, g, r = cv2.split(m)
ib = np.array(b)
p1,q1 = ib.shape[:2]
h1 = p1*q1
ib = np.reshape(ib,(h1,1))
b = b/np.max(ib)
ig = np.array(g)
p2,q2 = ig.shape[:2]
h2 = p2*q2
ig = np.reshape(ig,(h2,1))
g = g/np.max(ig)
ir = np.array(r)
p3,q3 = ir.shape[:2]
h3 = p3*q3
ir = np.reshape(ir,(h3,1))
r = r/np.max(ir)
wls1 = wlsFilter(b,1)
wls2 = wlsFilter(g,1)
wls3 = wlsFilter(r,1)
wls = cv2.merge([wls1, wls2, wls3])
cv2.imshow('image', img)
cv2.imshow('filter', wls)
cv2.imwrite(r'C:\Users\x\Desktop\18.jpg', wls)
cv2.waitKey(0)
cv2.destroyAllWindows()