论文翻译——vChain: Enabling Verifiable Boolean Range Queries over Blockchain Databases

0-abstract

由于加密货币的兴起和去中心化应用的兴起，区块链近来备受关注。查询存储在区块链数据库中的数据的需求不断增长。为了确保查询的完整性，用户可以维护整个区块链数据库并在本地查询数据。但是，由于区块链的巨大数据量和巨大的维护成本，这种方法即使不可行也不可行。在本文中，我们迈出了调查区块链数据库上可验证查询处理问题的第一步。我们提出了一种名为vChain的新颖框架，该框架可减轻用户的存储和计算成本，并采用可验证的查询来确保结果的完整性。为了支持可验证的布尔范围查询，我们提出了一种基于累加器的经过身份验证的数据结构，该结构可对任意查询属性进行动态聚合。进一步开发了两个新索引来聚合块内和块间数据记录，以进行有效的查询验证。我们还提出了倒置前缀树结构，以同时加速大量订阅查询的处理。安全分析和实证研究验证了所提出技术的鲁棒性和实用性。

1 INTRODUCTION

由于比特币[1]和以太坊[2]等加密货币的成功，近年来，区块链技术获得了压倒性的势头。区块链是仅附加的数据结构，它分布式存储在网络中的对等点之间。尽管网络中的对等方可能不会相互信任，但是区块链从两个方面确保了数据完整性。首先，借助哈希链技术，存储在区块链上的数据是不可变的。其次，由于其共识协议，区块链可确保所有对等方都维护相同的数据副本。这些受密码保护的安全机制，再加上区块链的去中心化和出处属性，使区块链成为改变数据库系统的潜在技术[3、4、5、6、7]。

从数据库的角度来看，区块链可以看作是存储大量带时间戳数据记录的数据库。随着区块链广泛用于金融，供应链和IP权利管理等数据密集型应用，用户对查询存储在区块链数据库中的数据的需求日益增加。例如，在比特币网络中，用户可能希望找到满足各种范围选择谓词的交易，例如“交易费≥50美元”和“ 0.99万美元≤总产出≤101万美元” [8]。在基于区块链的专利管理系统中，用户可以使用布尔运算符在专利摘要中搜索关键字的组合，例如“区块链”∧（“查询”∨“搜索”）[9]。许多公司，包括数据库巨头IBM、Oracle和SAP，以及诸如FlureeDB[10]、BigchainDB[11]和SwarmDB[12]等初创公司，都致力于开发区块链数据库解决方案，以支持类似SQL的查询，所有这些都假设存在可信的一方，该可信方可以忠实地执行基于块链数据库的物化视图的用户查询。但是，这种受信方可能并不总是存在，并且无法保证查询结果的完整性。具有完整性保证的查询处理在区块链研究中仍然是一个尚未探索的问题。

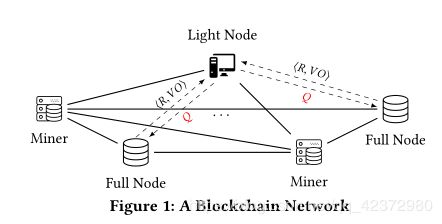
在典型的区块链网络[1、2]，1中，存在三种类型的节点，如图1所示：完整节点，矿工和轻型节点。一个完整的节点将所有数据存储在区块链中，包括块头和数据记录。矿工是一个具有强大计算能力的完整节点，负责构建共识证明（例如，比特币区块链中的随机数）。轻节点仅存储块标头，其中包括共识证明和块的加密哈希。请注意，数据记录未存储在灯光节点中。

、

为了确保通过区块链数据库进行查询的完整性，查询用户可以作为完整节点加入区块链网络。然后，用户可以下载并验证整个数据库并在本地处理查询，而不会影响查询的完整性。但是，维护整个数据库的完整副本对于普通用户而言可能会过于昂贵，因为它需要大量的存储，计算和带宽资源。例如，运行一个比特币完整节点的最低要求包括200GB的可用磁盘空间，不限流量的宽带连接，至少每秒50KB的上传速度以及每天6个小时的运行时间[13]。为了迎合资源有限的用户（尤其是移动用户）的需要，一种更具吸引力的替代方法是将存储和查询服务委派给功能强大的完整节点，而查询用户仅充当接收结果的轻型节点。尽管如此，如何确保查询结果的完整性仍然是一个挑战，因为完整的节点不受信任，这是区块链的固有假设。

为了解决上述查询完整性问题，在本文中，我们提出了一个名为vChain的新颖框架，该框架采用可验证的查询处理来保证结果的完整性。更具体地说，我们在每个块上增加了一些其他的认证数据结构（ADS），基于此结构，（不受信任的）完整节点可以构造并返回密码证明，称为验证对象（VO），以供用户验证每个结果查询。查询用户（lightnode）和完整节点之间的通信如图1所示，其中Q表示查询请求，R表示结果集。

值得注意的是，此vChain框架的灵感来自为外包数据库研究的查询身份验证技术[14、15、16、17、18]。但是，存在一些关键差异，使常规技术不适用于区块链数据库。首先，常规技术依靠数据所有者使用私钥对ADS进行签名。相反，在区块链网络中没有数据所有者。只有矿工才能根据共识协议构造共识证明，将新数据追加到区块链。但是，它们不能充当数据所有者，因为它们无法持有私钥并签署ADS。其次，传统的ADS建立在固定的数据集上，并且这种ADS无法有效地适应数据不受限制的区块链数据库。第三，在传统的外包数据库中，总是可以根据需要生成并附加新的ADS，以支持涉及不同属性集的更多查询。但是，由于区块链的不可变性，这将是困难的，在这种情况下，更需要一种适合所有情况的ADS以支持动态查询属性。

显然，ADS的设计是vChain框架的关键问题。为了解决这个问题，本文着重于布尔范围查询，如前所述，布尔范围查询通常在区块链应用程序中发现[8，9]。我们提出了一种新颖的基于累加器的ADS方案，该方案可对任意查询属性（包括数值属性和集合值属性）进行动态汇总。这种新设计的ADS独立于共识协议，因此与当前的区块链技术兼容。在此基础上，开发了有效的可验证查询处理算法。我们还针对块内数据和块间数据分别提出了两种经过身份验证的索引结构，以实现批量验证。为了支持大规模订阅查询，我们进一步提出了可以将相似查询请求分组的查询索引方案。总而言之，我们在本文中所做的贡献如下：

• 据我们所知，这是可验证查询处理的第一项工作，它利用内置的ADS来实现区块链数据库的查询完整性。
• 我们提出了一个新颖的vChain框架，以及一个新的ADS方案和两个索引结构，可以聚合块内和块间数据记录，以进行有效的查询处理和验证。
• 我们开发了一个新的查询索引，它可以同时处理大量的订阅查询。
• 我们进行了安全性分析以及实证研究，以验证所提出的技术。我们还将解决实际的实施问题。

本文的其余部分安排如下。第2节回顾了有关区块链和可验证查询处理的现有研究。第3节介绍了正式的问题定义，第4节介绍了密码原语。第5节介绍了我们的基本解决方案，然后通过第6节设计的两个索引结构对其进行了改进。第7节讨论了可验证的订阅查询。介绍了安全性分析。在第8节中，第9节介绍了实验结果。最后，我们在第10节中总结我们的论文。

2 RELATED WORK

在本节中，我们简要回顾相关研究并讨论相关技术。

区块链。自从引入比特币加密货币以来，区块链技术已受到学术界和工业界的相当关注[1,2,5]。区块链本质上是Merkle哈希树（MHT）[19]的一种特殊形式，被构造为一系列的块。如图2所示，每个块存储一个交易记录列表和一个基于它们的MHT。每个块的头由四个部分组成：（i）PreBkHash，它是前一个块的哈希； （ii）TS，即创建块时的时间戳； （iii）ConsProof，由矿工构建并保证区块共识。 （iv）MerkleRoot，它是MHT的根哈希。 ConsProof通常是根据PreBkHash和MerkleRoot计算的，并根据共识协议而有所不同。在广泛使用的工作量证明（PoW）共识协议中，ConsProof是由矿工计算的随机数，使得：
hash（PreBkHash | TS | MerkleRoot | nonce）≤Z
其中Z对应于挖掘难度。矿工发现随机数后，它将打包新块并将其广播到整个网络。其他矿工验证交易记录和新区块的随机数，并在验证后将其追加到区块链上。

为了解决区块链系统的各种问题，已经做出了巨大的努力，包括系统协议[20,21]，共识算法[22、23]，安全性[24、25]，存储[7]和性能基准测试[4]。最近，包括IBM [26]，Oracle [27]和SAP [28]在内的主要数据库供应商都已将区块链与他们的数据库管理系统集成在一起，并且它们允许用户通过数据库前端在区块链上执行查询。此外，许多初创公司，例如FlureeDB [10]，BigchainDB [11]和SwarmDB [12]，都在为分散式应用程序开发基于区块链的数据库解决方案。但是，它们通常将查询处理与基础区块链存储区分开来，并依靠受信任的数据库服务器来确保查询完整性。相比之下，我们提出的vChain解决方案将经过身份验证的数据结构构建到了区块链结构中，因此，即使是不受信任的服务器也可以提供完整性保证的查询服务。

可验证的查询处理。已对可验证查询处理技术进行了广泛研究，以确保针对不受信任的服务提供商的结果完整性（例如[14、15、16、17、18、29]）。现有的大多数研究都集中在外包数据库上，并且有两种典型的方法：使用基于电路的可验证计算（VC）技术支持常规查询，以及使用经过验证的数据结构（ADS）支持特定查询。基于VC的方法（例如SNARKs [30]）可以支持任意计算任务，但要付出很高的代价，有时甚至是不切实际的开销。而且，这需要昂贵的预处理步骤，因为数据和查询程序都需要硬编码到证明密钥和验证密钥中。为了解决这个问题，Ben-Sasson等人。 [31]开发了SNARK的变体，其中预处理步骤仅取决于数据库和查询程序的上限大小。最近，Zhang等。 [29]提出了一种vSQL系统，该系统利用交互式协议来支持可验证的SQL查询。但是，它仅限于具有固定模式的关系数据库。

相比之下，基于ADS的方法通常针对特定查询进行定制时效率更高。我们提出的解决方案属于这种方法。通常将两种类型的结构用作ADS：数字签名和MHT。数字签名基于非对称密码认证数字消息的内容。为了支持可验证的查询，它要求对每个数据记录进行签名，因此无法扩展到大型数据集[14]。另一方面，MHT建立在分层树上[19]。叶节点中的每个条目都分配有数据记录的哈希摘要，而内部节点中的每个条目都分配了从子节点派生的摘要。数据所有者对MHT的根摘要进行签名，该根摘要可用于验证数据记录的任何子集。 MHT已广泛适用于各种索引结构[15、16、17]。最近，已经有关于集值数据的可验证查询的研究[32，33，34，35，36]。

另一个密切相关的研究领域是对数据流的可验证查询处理[37、38、39、40]。但是，以前的研究[38,39]集中于一次性查询以检索流数据的最新版本。 [40]要求数据所有者为所有数据记录维护一个MHT，并且存在较长的查询等待时间，这不适用于实时流服务。另一方面，在[41,42,43]中已经研究了对数据流的订阅查询。到目前为止，还没有工作考虑过区块链数据库订阅查询的完整性问题。

3 PROBLEM DEFINITION

如第1节所述，本文提出了一种新颖的vChain框架，并研究了区块链数据库上的可验证查询处理。图3显示了vChain的系统模型，它涉及三个方面：（i）矿工，（ii）服务提供商（SP）和（iii）查询用户。矿工和SP都是维护整个区块链数据库的完整节点。查询用户是一个轻量级节点，仅跟踪块头。矿工负责构建共识证明并将新的区块添加到区块链。 SP向轻量级用户提供查询服务。

可以将存储在区块链中的数据建模为一系列临时对象{o1，o2，...，on}。每个对象oi用ti，Vi，Wi Wi表示，其中t i是对象的时间戳，Vi是表示一个或多个数值属性的多维矢量，而Wi是设置值的属性。为了实现可验证的查询处理，矿工将构造一个经过身份验证的数据结构（ADS）并将其嵌入每个块中（将在第5-7节中进行详细介绍）。我们考虑两种形式的布尔范围查询：（历史）时间窗口查询和订阅查询。

时间窗口查询。用户可能希望搜索在特定时间段内出现的记录。在这种情况下，可以发出时间窗口查询。具体而言，时间窗口查询的形式为q =〈[ts，te]，[α，β]，ϒ〉，其中[ts，te]是该时间段的时间范围选择谓词[α， β]是数字属性的多维范围选择谓词，ϒ是设置值属性上的单调布尔函数。结果，SP返回所有对象，使得{oi =〈ti，Vi，Wi〉| ti∈[ts，te]∧Vi∈[α，β]∧（Wi）= 1}。为简单起见，我们假设ϒ是合取范式（CNF）。

Example3.1 在比特币交易搜索服务中，每个对象oi对应一个硬币转移交易。它由存储在Vi中的传输量和存储在Wi中的一组发送者/接收者地址组成。用户可以发出查询q =〈[2018-05,2018-06]，[10，+∞]，发送：1FFYc∧接收：2DAAf〉以查找从2018年5月到6月发生的所有交易大于10且与地址“ send：1FFYc”和“ receive：2DAAf”关联的值。

订阅查询。除了时间窗口查询之外，用户还可以通过订阅查询来注册其兴趣。具体而言，订阅查询的形式为q = 〈−，[α，β]，ϒ〉，其中[α，β]和ϒ与时间窗口查询中的查询条件相同。反过来，SP连续返回所有对象，使得{oi =〈ti，Vi，Wi〉| Vi∈[α，β] ϒ（Wi）= 1}，直到注销查询为止。

Example3.2 在基于区块链的汽车租赁系统中，每个租赁对象oi包含一个存储在Vi中的租赁价格和一组存储在Wi中的文本关键字。用户可以订阅查询q =〈-，[200，250]，“ Sedan”∧（“ Benz”∨“ BMW”）〉以接收全部
价格在[200，250]范围内且包含关键字“ Sedan”和“ Benz”或“ BMW”的租赁消息。

时间窗口查询和订阅查询的其他示例可以在图3中找到。

威胁模型。我们认为SP作为区块链网络中不受信任的对等方可能是潜在的对手。由于
由于程序故障，安全漏洞和商业利益等各种问题，SP可能会返回篡改或不完整的查询结果，从而违反了区块链的预期安全性。为了解决这种威胁，我们采用可验证的查询处理，使SP能够证明查询结果的完整性。具体而言，在查询处理期间，SP检查嵌入在区块链中的ADS，并构造一个包含结果验证信息的验证对象（VO）。 VO与结果一起返回给用户。使用VO，用户可以根据以下条件确定查询结果的完整性和完整性：

• 健全。结果返回的对象均未被篡改，并且所有对象都满足查询条件。
• 完整性。关于查询窗口或订阅期，没有缺少有效的结果。

当我们在第8节中进行安全性分析时，上述安全性概念将被形式化。

该模型的主要挑战是如何设计ADS，以便可以轻松地将其存储在区块链结构中，同时可以针对时间窗口查询和订阅高效构建具有成本效益的VO（导致较小的带宽开销和快速的验证时间）查询。我们将在接下来的几节中应对这一挑战。

4 PRELIMINARIES

本节对算法设计中需要的密码结构进行了初步介绍。

加密哈希函数。密码哈希函数hash（·）接受任意长度的字符串作为其输入，并返回固定长度的位字符串。它具有抗冲突性，并且很难找到两个不同的消息m 1和m 2，因此hash（m 1）= hash（m 2）。经典的加密哈希函数包括SHA-1，SHA-2和SHA-3系列。

双线性配对。令G和H为两个具有相同素数p的循环乘法组。令g为G的生成器。双线性映射是具有以下属性的函数e：G×G→H：

双线性配对是多集累加器的基本操作，如本文稍后所述。

q-强Diffie-Hellman（q-SDH）假设[44]。令pub =（p，G，H，e，g）是如上所述的双线性配对。它指出，对于所有多项式q和所有概率多项式时间的对手Adv，

q-Diffie-Hellman指数（q-DHE）假设[45]。如上所述，使pub =（p，G，g）。它指出，对于所有多项式q和所有概率多项式时间的对手Adv，

加密多集累加器。多重集是集合的概括，其中元素可以多次出现。为了以恒定大小表示它们，密码多集累加器是函数acc（·），它以抗碰撞的方式将多集映射到某个循环乘法组中的元素[36]。

累加器的一个有用特性是可以用来证明集合不相交。它由以下概率多项式时间算法组成：

蓄能器的更详细的构造和不相交的证明将在5.2节中给出。

5 BASIC SOLUTION

为了在我们的vChain框架中启用可验证的查询，天真的方案是将传统的MHT构造为每个块的ADS，并应用基于MHT的常规身份验证方法。但是，这种幼稚的方案具有三个主要缺点。首先，MHT仅支持在其上构建了Merkle树的查询键。为了支持涉及任意属性集的查询，需要为每个块构造指数级的MHT。其次，MHT不适用于集值属性。第三，不同区块的MHT无法有效地聚合，因此无法利用区块间优化技术。为了克服这些缺点，在本节中，我们基于新的基于累加器的ADS方案提出了新颖的身份验证技术，该技术将数字属性转换为集值属性，并能够对任意查询属性进行动态聚合。

在下文中，我们从考虑单个对象开始，并着重于布尔时间窗口查询，以简化说明（第5.1和5.2节）。然后，我们将其扩展到范围查询条件（第5.3节）。我们将在第6节中讨论对多个对象的批处理查询处理和验证。在第7节中将详细介绍订阅查询。

5.1 ADS Generation and Query Processing

为简单起见，本节仅考虑对设置值属性Wi的布尔查询条件。我们假设每个块都存储一个对象，然后使用ObjectHash表示原始块结构中的MerkleRoot（图2）。

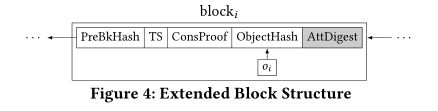
ADS生成。回想一下，在提出的vChain框架中，在挖掘过程中会为每个块生成一个ADS。 SP可以使用它为每个查询构造一个验证对象（VO）。为此，我们通过添加一个名为AttDigest的额外字段来扩展原始的块结构，如图4中阴影部分所示。因此，块头由PreBkHash，TS，ConsProof，ObjectHash和AttDigest组成。

要用作ADS，AttDigest应该具有三个所需的属性。首先，AttDigest应该能够以一种可以用来证明对象是否符合查询条件的方式来汇总对象的属性Wi。如果不匹配，我们可以只返回此摘要而不是整个对象。其次，无论Wi中元素的数量如何，AttDigest的大小都应恒定。第三，AttDigest应该是可聚合的，以支持对块内甚至跨块的多个对象进行批量验证（第6节）。因此，我们建议使用多集累加器作为AttDigest：

尽管在第4节中已经描述了它支持的功能，包括ProveDisjoint（·）和VerifyDisjoint（·），但是为了更好的可读性，我们将详细的构造推迟到5.2节。

可验证的查询处理。给定布尔查询条件和数据对象，只有两种可能的结果：匹配或不匹配。通过返回对象作为结果，可以很容易地验证第一种情况的健全性，因为它的完整性可以通过存储在块头中的ObjectHash进行验证，这对于轻型节点上的查询用户是可用的（请参见图3）。 。挑战在于如何通过使用AttDigest有效地验证第二种情况。由于CNF是用“或”运算符的AND列表表示的布尔函数，因此我们可以将CNF中的布尔函数视为集合列表。例如，查询条件“ Sedan”∧（“ Benz”∨“ BMW”）等效于两个集合：{“ Sedan”}和{“ Benz”，“ BMW”}。考虑一个不匹配的对象o i：{“ Van”，“ Benz”}。不难发现，存在一个等价集（即{“ Sedan”}），使得它与对象属性的交集为空。因此，我们可以应用ProveDisjoint（{“ Van”，“ Benz”}，{“ Sedan”}，pk）生成不相交的证明π作为不匹配对象的VO。因此，用户可以从块标题中检索AttDigesti = acc（{“ Van”，“ Benz”}）并使用VerifyDisjoint（AttDigest i，acc（{“ Sedan”}），π，pk）来验证不匹配。整个过程在算法1中有详细说明。

扩展上述算法以支持时间窗口查询很简单。该过程基本上找到时间戳在查询窗口内的相应块，并为这些选定块中的每个对象重复调用算法1。例如，假设查询布尔函数为“ Sedan”∧（“ Benz”∨“ BMW”）。时间窗口内的对象列表包括o1：{“ Sedan”，“ Benz”}，o2：{“ Sedan”，“ Audi”}，o3：{“ Van”，“ Benz”}和o4： {“ Van”，“ BMW”}。 SP可以将ProveDisjoint（·）应用于o2，o3和o4，以证明它们分别不符合条件“ Benz”∨“ BMW”，“ Sedan”和“ Sedan”。至于o1，由于匹配，SP将直接返回对象。

5.2 Constructions of Multiset Accumulator

现在，我们将在5.1节中讨论用作AttDigest的多集累加器的两种可能的构造。每种构造都有其自身的优点和缺点，并且适合于不同的应用场景，我们将在第9节中看到。

5.2.1构造1.我们首先提出[32]中提出的构造，该构造基于双线性配对和q -SDH假设。它由以下算法组成。

5.2.2构造2.受[35]的启发，第二种构造建议引入两个额外的Sum（·）和Proof-Sum（·）原语，它们允许聚合多个累加值或设置不相交的证明。它基于双线性配对和q -DHE假设，由以下算法组成。

与构造1相比，构造2支持多个累计值的聚合或设置不相交的证明，可用于6.3节中的在线批处理验证方法。但是，它导致更大的密钥大小。特别是，构造1中的公钥大小与最大多集大小成线性关系，而在构造2中，公钥大小与系统中属性的最大可能值成线性关系。在实际应用中，常见的做法是使用加密哈希函数将每个属性值编码为整数，然后由累加器接受。由于典型的哈希函数返回的值以数百位为单位，因此以这种比例提前生成和发布公钥是昂贵的。为了解决此问题，我们可能会引入一个受信任的oracle，该oracle拥有秘密密钥并负责回答公共密钥的请求。可以由受信任的第三方代理或使用诸如SGX之类的安全硬件来实现这种预言。

5.3 Extension to Range Queries

前面的部分主要考虑对集值属性Wi的布尔查询。在许多情况下，用户还可以将范围条件应用于数字属性Vi。为了解决这个问题，我们提出了一种将数值属性转换为集值属性的方法。然后，范围查询可以相应地映射到布尔查询。

这个想法如下。首先，我们用二进制格式表示每个数值。接下来，我们将数值转换为一组二进制前缀元素（表示为函数trans（·））。例如，值4可以二进制格式100表示​​。因此，可以将其转换为前缀集，即trans（4）= {1 *，10 *，100}，其中*表示通配符匹配运算符。类似地，对于数值向量，我们可以对每个维度应用上述过程。例如，向量（4，2）具有二进制格式（100，010）。因此，其变换后的前缀集为{1 ∗ 1，10 ∗ 1，100 1，0 ∗ 2，01 ∗ 2,010 2}。请注意，此处每个元素都有一个下标符号（即1和2），用于在向量的不同维度上区分二进制值。

接下来，我们通过使用在整个二进制空间上构建的二进制树，将范围查询条件转换为单调布尔函数（例如，图5显示一维空间树[0,7]）。具体来说，对于一维范围[α，β]，我们首先以其二进制格式表示α和β。接下来，我们将α和β视为树中的两个叶节点。最后，我们找到最小的树节点集以精确覆盖整个范围[α，β]。转换后的布尔函数是使用OR（∨）语义将集合中的每个元素连接在一起的函数。例如，对于查询范围[0,6]，我们可以找到其转换后的布尔函数为0 * 10 * 110（请参见图5中的灰色节点）。如第5.1节所述，此布尔函数的等价集为{0 ∗，10 ∗，110}。类似地，在多维范围的情况下，转换后的布尔函数是使用AND（）语义将每个维度的部分布尔函数连接在一起的函数。例如，查询范围[（0，3），（6，4）]可以转换为（0 * 1∨10 * 1∨110 1）∧（011 2∨100 2

通过上述转换，对数值v i是否在[α，β]范围内的查询将成为布尔对v i的转换后的前缀集与[α，β]的等价集进行布尔查询。在上述示例中，由于{1 ∗，10 ∗，100}∩{0 ∗，10 ∗，110} = {10 ∗}，4，4∈[0，6]; （4，2）<[（0,3），（6，6，4）]因为存在一些等价集{011 2，100 2}使得{011 2，100 2}∩{1 * 1，10 * 1 ，100 1，0 ∗ 2，01 ∗ 2，010 2} =∅。

由于采用了数据转换技术，因此我们在续篇中将这两种类型的查询条件统一为集合值属性上的统一布尔查询条件。更具体地说，对于每个数据对象〈ti，Vi，Wi〉，将其转换为元组〈ti，Wi''，其中Wi'= trans（V i）+ W i；然后将查询q =〈[ts，te]，[α，β]，ϒ〉转换成〈[ts，te]，ϒ'〉，其中ϒ'= trans（[α，β]）∧。因此，查询结果为{oi =〈ti，Wi'〉| ti
∈[ts，te]∧'（Wi'）= 1}。

6 BATCH VERIFICATION

在本节中，我们讨论如何通过批处理验证来提高查询性能。我们首先介绍两个经过身份验证的索引结构，即块内索引（第6.1节）和块间索引（第6.2节），然后介绍一种在线批处理验证方法（第6.3节）。所有这些技术使SP可以批量证明对象不匹配。

6.1 Intra-Block Index

在前面的讨论中，为简单起见，我们假定每个块仅存储一个对象。通常，每个块通常存储多个对象。天真的，我们可以对每个对象重复应用单对象算法以确保查询的完整性，但是这会导致验证复杂度与对象数量成线性关系。此外，可以观察到，如果两个对象共享某个公共属性值，则由于相同的部分查询条件，它们可能会与某些查询不匹配。因此，为了减少校对和验证的开销，我们提出了一种块内索引，它可以聚合多个对象并提高性能。

图6显示了具有块内索引的区块链块。它将每个对象的ObjectHash和AttDigest组织为二进制Merkle树。块头包括
以下组件：PreBkHash，TS，ConsProof和MerkleRoot，其中MerkleRoot是二进制Merkle树的根哈希。每个树节点具有三个字段：子哈希（由哈希i表示，并用于形成MHT），属性多集（由Wi表示）和属性多集的累积值（由AttDigest i表示）。它们是根据子节点计算的，如下所示。

定义6.1（Intra-BlockIndexNon-LeafNode）。令hash（·）为加密哈希函数，‘| ’是字符串连接运算符，acc（·）是多集累加器，n l和nr分别是节点n的左子元素和右子元素。非叶子节点n的字段定义为：

定义6.2（块内索引叶节点）。叶节点的字段与基础对象的字段相同。

在构建块内索引时，我们希望实现最大的打样效率。也就是说，我们旨在最大程度地在查询处理期间将不匹配的对象修剪到一起的机会。一方面，这意味着我们应该找到一种集群策略，以便在给定用户查询的情况下，节点与查询不匹配的机会最大。换句话说，我们努力使每个节点下对象的相似性最大化。另一方面，平衡树是优选的，因为它可以提高查询效率。因此，我们建议以区块链矿工自下而上的方式基于区块的数据对象建立区块内索引。首先，将块中的每个数据对象分配给叶节点。接下来，产生最大Jaccard相似度的叶子节点迭代合并。这两个合并的树节点用于在上层创建一个新的非叶节点。在每个级别重复此过程，直到创建根节点为止。最后，由hashr分配的Merkle-Root被写入为块标题的组件之一。算法2详细显示了该过程。

利用上述块内索引，SP可以将查询作为树搜索进行处理。从根节点开始，如果当前节点的属性多集满足查询条件，则将进一步探索其子树。同样，将相应的AttDigest添加到VO，它将在结果验证期间用于重建MerkleRoot。另一方面，如果多集不满足查询条件，则意味着所有基础对象都不匹配。在这种情况下，SP将使用相应的AttDigest调用ProveDisjoint（·）以生成不匹配证明。到达叶节点后，其多重集满足查询条件的对象是匹配对象，并将作为查询结果返回。算法3示出了使用块内索引的VO构造。

为了说明起见，我们使用与第5.1节中讨论的对象相同的对象集。块内索引在图6中示出。来自用户的布尔查询是“ Sedan”∧（“ Benz”∨“ BMW”）。查询过程只是将索引从根节点遍历到叶节点。查询结果为{o1}。 SP返回的VO包括{〈AttDigestr〉，〈AttDigest5〉，〈hash2，π2，{“ Audi”}，AttDigest2〉，〈hash6，π6，{“ Van”}，AttDigest6〉}。此处π2和π6分别是失配节点N2和N6的两个不相交的证明（图6中阴影部分）。请注意，AttDigestr和AttDigest5将仅用于在结果验证期间重建MerkleRoot。在用户方面，不匹配验证通过使用VO中的AttDigest，不相交集和证明π调用VerifyDisjoint（·）来工作。此外，为了验证结果的正确性和完整性，要求用户重建MerkleRoot并将其与从块头读取的内容进行比较。在我们的示例中，首先，使用〈π2，AttDigest 2，{“ Audi”}〉和〈π6，AttDigest6，{“ Van”}〉调用VerifyDisjoint（·）以证明节点N2和N6确实与查询不匹配。此后，用户使用返回的结果计算hash（o1），并基于VO计算hash5 = hash（hash（o1）| hash2 | AttDigest5），hashr = hash（hash5 | hash6 | AttDigestr）。最后，用户对照块标题中的MerkleRoot检查新计算的哈希值。

6.2 Inter-Block Index

除了相同块内的相似对象外，跨块的对象也可能由于相似原因而共享相似性并与查询不匹配。基于此观察，我们构建了一个块间索引，该索引使用跳过列表来进一步优化查询性能。

如图7所示，块间索引由多个跳过组成，每个跳过都以指数形式增加前一个块。例如，列表可以跳过前面的2，4，8…块。对于每个跳过，它都维护三个组成部分：所有跳过块的哈希（由PreSkippedHash Lk表示），跳过块的属性多集之和（由W L k表示）和相应的累积值w.r.t。 WLk（用AttDigest L k表示）。请注意，这里我们使用属性多集的总和来启用第7节中的在线聚合身份验证。最后，使用额外的字段SkipListRoot将块间索引写入到块中，该字段定义为：

在查询处理期间，合格的跳过可用于表示由于不匹配的相同原因而对查询结果无贡献的多个块。由于用户可以避免访问这些跳过的块，因此可以降低验证成本。

算法4示出了具有块间索引的查询处理过程。我们从查询时间窗口中的最新块开始。我们将跳跃列表从最大跳跃迭代到最小跳跃。如果跳过WLi的多重集与查询条件不匹配，则意味着当前块和先前的第i个块之间的所有跳过块都不包含匹配结果。因此，将调用ProveDisjoint（·）并输出不匹配证明πi。然后，将〈PreSkippedHashL i，πi，ϒ i，AttDigest L i〉添加到VO。用户可以使用该证明来验证跳过的块确实与查询不匹配。同时，除了哈希L i之外的其他哈希也被添加到VO。如果在迭代过程中未能找到不匹配的块，则为当前块调用函数IntraIndexQuery（·）（算法3），然后再检查前一个块。如果我们成功找到不匹配跳过，则接下来将检查相应的前面的块。递归调用函数InterIndexQuery（·），直到我们完成检查查询窗口中的所有块为止。注意，我们可以结合块内索引和块间索引来最大化性能，因为它们没有冲突。

6.3 Online Batch Verification

回想一下，提出的块内索引尝试以最大化不匹配对象的证明效率的方式对同一块的对象进行聚类。然而，在不同块或什至同一块的不同子树中建立索引的某些对象/节点也可能共享失配的相同原因。因此，在线收集此类对象/节点以进行更有效的打样将是有益的。为此，可以应用构造2在5.2节中引入的Sum（·）原语，该原语在给定多个累加值时输出累加多集的累加值。在图6所示的运行示例中，假设o 2和o 4具有不匹配查询条件（“ Benz”）的相同原因。然后，SP可以返回π= ProveDisjoint（W2 + W4，{“ Benz”}，pk）和AttDigest 2,4 = Sum（acc（W2），acc（W4））。用户可以应用VerifyDisjoint（AttDigest 2,4，acc（{“ Benz”}），π，pk）来证明这两个对象成批不匹配。

7 VERIFIABLE SUBSCRIPTION QUERIES

订阅查询由查询用户注册，并被连续处理，直到注销为止。看到新确认的阻止后，SP将需要将结果与VO一起发布给注册用户。在本节中，我们首先提出一个查询索引，以有效处理大量的订阅查询（第7.1节）。之后，我们开发了一种惰性身份验证优化，该优化可延迟不匹配证明以减少查询验证成本（第7.2节）。

7.1 Query Index for Scalable Processing

如前所述，大部分查询处理开销来自生成SP处对象不匹配的证明。幸运的是，不匹配的对象可能因不同的订阅查询而具有不匹配的相同原因。因此，这种查询可以共享不匹配证明。受[41]的启发，我们建议在订阅查询上构建一个倒置的前缀树，称为IP-Tree。它本质上是一个前缀树，在数字范围条件和布尔设置条件方面都引用了反向文件。

前缀树组件。为了索引所有订阅查询的数值范围，IP树是基于网格树构建的，因此每个树节点都由CNF布尔函数表示（请参见第5.3节）。例如，对应于左上单元（[0，2]，[1，3]）的图8中的网格节点N1由{0 *1∧1* 2}表示。前缀树的根节点覆盖所有订阅查询的整个范围空间。

反向文件组件。 IP树的每个节点都与一个反向文件关联，该文件是基于在该节点下建立索引的订阅查询构造的。每个反向文件都有两个子组件：

• 范围条件反转文件（RCIF）。 RCIF中的每个条目都有两个属性：查询q i及其封面类型（即全部或部分）。 RCIF中的所有查询都与节点的数字空间S相交。封面类型指示q i是完全覆盖S还是部分覆盖S。 RCIF用于检查数值范围条件的不匹配。
• 布尔条件反转文件（BCIF）。 BCIF仅记录完全覆盖节点空间的查询。 BCIF中的每个条目都包含两个属性：查询条件集ϒ和相应的查询。 BCIF用于检查布尔设置条件的不匹配。

我们以图8为例来说明如何构造IP树。它由SP以自上而下的方式构建。我们首先创建根节点，并将所有查询作为部分覆盖查询添加到其RCIF中。然后，我们分割根节点并创建四个等距的子节点。对于每个子节点，如果查询完全或部分覆盖了节点的空间，它将被添加到节点的RCIF中。此外，完全覆盖查询的等价集也将添加到节点的BCIF中。以N1为例。虽然查询q 1和q 2完全覆盖了此节点，但是查询q 3仅部分覆盖了该节点。因此，RCIF包含三个交集查询q1，q2和q3。 q1和q2的封面类型已满，而q3的封面类型是部分。对于N1的BCIF，q1和q2共享等效集{“ Van”}，而集{“ Benz”}和{“ BMW”}分别对应于查询q1和q2。接下来，由于q3仅部分覆盖N1，因此我们将N1进一步分为四个子单元。由于q3完全覆盖了N7，因此将其添加到N7的RCIF和BCIF中。当在任何叶节点中未找到部分查询时，该算法终止。注册或注销查询后，我们会更新与查询数字范围相对应的IP树节点。如果需要，我们还可以拆分或合并树节点。请注意，为防止树变得过深，当树的深度达到某个预定义的阈值时，我们将切换回没有IP树的情况。

使用IP树索引，订阅查询可以作为树遍历来处理。我们首先使用单个对象的示例来说明基本概念。当新对象o到达时，沿着从根到覆盖o的叶节点的路径遍历IP树。对于遍历路径上的任何节点nq，可以从nq的RCIF中找到关联的查询。这些查询可分为三类：（1）全覆盖查询，其在nq的BCIF中的等价集匹配o（因此，此查询添加了o）； （2）一个完全覆盖的查询，其等效集在nq的BCIF不匹配o中被调用（因此，调用ProveDisjoint（·），并为此查询生成不相交的证明）； （3）部分覆盖查询（无需采取进一步措施）。此外，我们还确定了出现在nq的父级RCIF中而不是nq的查询。这些查询与o的数值范围条件不匹配，因此也为它们生成了不相交的证明。接下来，将处理nq的子节点，此过程将一直持续到我们到达叶节点或所有查询被分类为匹配或不匹配为止。考虑一个新的对象oi =〈ti，（0，2），{“ Van”，“ Benz”}〉=〈ti，{001，102，“ Van”，“ Benz”}如图8所示。在N1 ，由于布尔设置条件和数值范围条件，q1被归类为匹配查询，q2和q4不匹配，而q3直到我们检查N1的子节点N7才被确认为不匹配。

这个想法可以很容易地扩展到由块内索引索引的新对象块。我们从块内索引的根开始。对于任何索引节点nb，我们将其视为超对象，并应用上述查询处理过程。唯一的区别是，如果将完全覆盖的查询分类为匹配，则我们不能立即返回当前节点n b作为查询结果，而是进一步递归检查其子节点，直到到达叶节点为止。为了节省空间，详细算法的伪代码在附录A中给出。

7.2 Lazy Authentication

观察到在上一节中，结果和证明会立即发布给注册用户，同时确认新的阻止。特别是，即使没有查询的匹配结果，也将计算并发送不匹配证明。这种方法适用于实时应用程序。对于不具有此类实时要求的应用程序，我们提出了一种惰性身份验证优化，其中SP仅在存在匹配对象（或自上一个结果以来经过阈值的时间）时才返回结果。

在这种方法中，VO应该证明当前对象是一个匹配项，而自上一个结果以来所有其他对象都与查询不匹配。为此，我们可以简单地等待匹配结果并调用时间窗口查询来动态计算不匹配证明。但是，此方法只能分别为每个查询生成不匹配证明，并且无法利用不同预订查询共享的证明。而且，这种方法将举证责任全部留给了匹配结果。为了解决这些问题，我们提出了一种新的方法，该方法利用块间索引逐渐生成不匹配证明。

使用块间索引来回答订阅查询与使用时间窗口查询完全不同，原因是我们可以向后遍历区块链并使用跳过列表在时间窗口查询中汇总证明。但是，对于预订查询，我们无法这样做，因为新块尚不可用，并且我们不知道将来的对象是否会共享相同的不匹配条件。因此，我们引入了一个堆栈，以方便跟踪共享相同失配条件的到达块。基本思想是使用跳过列表来找到最大跳过距离L i，以使其覆盖堆栈顶部的m个元素。这些块的AttDigests替换为AttDigest Li。多亏了5.2节中的构造2，可以通过调用ProofSum（·）在线合并不相交的证明。例如，我们在堆栈中有两个不匹配的blocki和blocki-1，并且有一个距离为2的跳跃。然后，SP可以用从ProofSum（πi，πi-1）计算的合计证明来代替它们的证明。这样，当找到匹配结果时，SP无需从头开始计算集合的不相交证明。详细过程在算法5中描述。

8 SECURITY ANALYSIS

本部分对多集累加器和查询身份验证算法执行安全性分析。

8.1 Analysis on Multiset Accumulators

我们首先给出多集累加器安全概念的正式定义，并设置不相交的证明。

定义8.1（不可伪造性[32]）。如果在以下实验中任何多项式时间的对手的成功概率都可以忽略不计，那么我们说多集累加器是不可伪造的：

此属性确保恶意SP伪造集合不相交证明的机会可以忽略不计，这为我们提出的查询身份验证算法的安全性奠定了基础。现在我们表明，我们的蓄能器结构确实满足了所需的安全性要求。

定理8.1。第5.2节中介绍的多集累加器的结构满足定义8.1中定义的不可伪造的安全性。

8.2 Analysis on Query Authentication

我们的查询认证算法不可伪造的正式定义如下：

定义8.2（不可伪造性）。我们说，如果在以下实验中任何多项式时间对手的成功概率都可以忽略不计，那么我们提出的查询认证算法是不可伪造的：

• 运行ADS生成并将所有对象{oi}交给对手；
• 对手输出查询q（时间窗口查询或订阅查询），结果R和VO；

我们说，如果VO通过了结果验证并且以下结果之一为真，则对手成功：

此属性确保恶意SP伪造错误或不完整结果的机会可以忽略不计。我们可以证明，我们提出的查询认证算法确实满足了所需的安全性要求。

定理8.2。我们提出的查询认证算法满足定义8.2中定义的不可伪造的安全性属性。

9 PERFORMANCE EVALUATION

在本节中，我们评估vChain框架在时间窗口查询和订阅查询中的性能。实验中使用了三个数据集：

• Foursquare（4SQ）[46]：4SQ数据集包含1M数据记录，这是用户签入信息。我们以30秒钟的间隔将记录打包为一个块，每个对象的格式为〈时间戳，[经度，纬度]，{检入地点的关键字}〉。平均而言，每条记录有2个关键字。
• 天气（WX）：WX数据集包含2012-2017年间美国，加拿大和以色列的36个城市的150万小时每小时天气记录。 2对于每条记录，它包含七个数字属性（例如湿度和温度）和一个天气描述属性，平均包含两个关键字。同一小时间隔内的记录打包为一个块。
• Ethereum（ETH）：ETH交易数据集是在2017年1月15日至2017年1月30日期间从以太坊区块链中提取的。3它包含90,000个区块和112万笔交易记录。每笔交易采用〈timestamp，amount，{addresss}〉的形式，其中amount是所转移的以太币的数量，而{addresses}是发送者和接收者的地址。大多数交易都有两个地址。

请注意，在4SQ，WX和ETH中，块的时间间隔分别大约为30s，1小时和15s。

查询用户是在具有Intel Core i5 CPU和8GB RAM的商用便携式计算机上设置的，并在CentOS 7上以单线程运行。 SP和Miner在具有双Intel Xeon 2.67GHz，X5650 CPU和32 GB RAM的x64刀片服务器上设置，在CentOS 7上运行。实验用C ++编写，并使用以下库：用于双线性配对计算的MCL ，用于模块算术运算的4 Flint，用于160位SHA-1哈希运算的Crypto ++和用于并行计算的OpenMP。此外，SP运行24个超线程以加速查询处理。

为了评估vChain中可验证查询的性能，我们主要使用三个指标：（i）以SP CPU时间为单位的查询处理成本，（ii）以用户CPU时间为单位的结果验证成本，以及（iii）VO的大小从SP传输到用户。对于每个实验，我们随机生成20个查询并报告平均结果。默认情况下，我们将数值范围的选择性设置为10％（对于4SQ和WX）和50％（对于ETH），并采用大小为3（对于4SQ和WX）和9（对于ETH）的析取布尔函数。 。对于WX，每个范围谓词都涉及两个属性。

9.1 Setup Cost

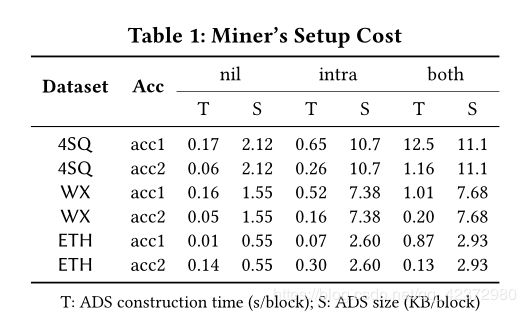
表1报告了矿机的安装成本，包括ADS的建造时间和ADS的大小。在我们的实验中比较了三种方法：（i）无：不使用索引； （ii）帧内：仅使用块内索引； （iii）两者：都使用块内索引和块内索引，其中，块间索引中的SkipList的大小设置为5。每种方法都采用两种不同的累加器结构（标有acc1和acc2）实现。在5.2节中。因此，每个实验中总共评估了六个方案。如预期的那样，两者的ADS构建时间通常都比无和内部的更长，但在大多数情况下仍在2s之内。此外，与acc1相比，acc2大大缩短了两者的构建时间，因为它支持在线聚合，因此可以在构建块间索引时重用前一个块的索引。关于ADS大小，它与所使用的累加器无关，对于不同的索引和数据集，其范围为每块2.6KB至11.1KB。

我们还测量了用户运行轻型节点以维护块标题所需的空间。对于nil和intra，无论数据集或累加器如何，每个块头的大小均为800位。由于块间索引，两者的块头大小都略微增加到960位。

9.2 Time-Window Query Performance

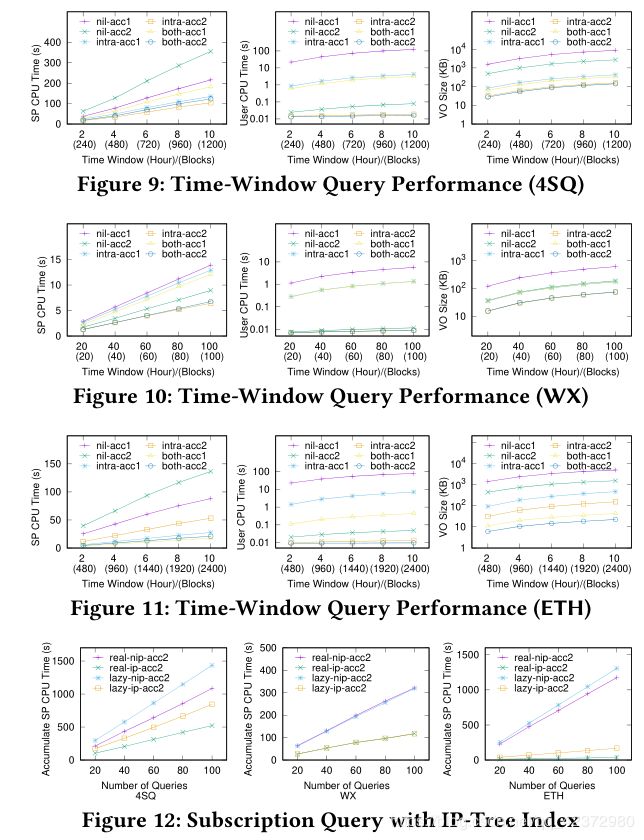
为了评估时间窗口查询的性能，我们将4SQ和ETH的查询窗口从2个小时更改为10个小时，将WX的查询窗口从20个小时更改为100个小时。这三个数据集的结果示于图1和2。 9-11。我们做了几个有趣的观察。首先，正如预期的那样，这些索引实质上改善了几乎所有指标的性能。特别是对于4SQ和ETH数据集，使用索引的性能至少比使用相同累加器但不使用任何索引的性能高2倍。这是因为这两个数据集中的对象共享较少的相似性，因此可以从使用索引进行修剪中受益更多。其次，基于索引的方案的成本仅随着查询窗口的扩大而线性增加。就使用acc 2的基于索引的方案的用户CPU时间而言，尤其如此，它支持不匹配的批量验证（请参见第6.3节）。第三，比较intra和两者，除了4SQ数据集的SP CPU时间外，两者始终不比intra更差。一方面，这表明使用块间索引的有效性。另一方面，两者均比SP CPU时间差的原因主要是因为在基于块间索引的方案中，较大的多集用作集合不相交证明的输入，这增加了SP CPU时间。附录D.3提供了对此的更多见解，在此我们研究了SkipList大小的影响。对于ETH数据集，两者都比intra的最大改进。原因如下。与4SQ相比，ETH中对象之间共享的相似度更低；与WX相比，ETH在每个块中包含的对象更少。对于这两种情况，通过使用块间索引中的跳过列表都可以提高性能。

9.3 Subscription Query Performance

接下来，我们评估订阅查询的性能。首先，我们在启用了块内索引和块间索引的默认设置下，检查有无SP使用IP树（表示为ip和nip）时SP的查询处理时间。我们随机生成不同数量的查询。我们将4SQ和ETH的默认订阅期设置为2小时，将WX设置为20小时。如图12所示，在所有测试情况下，IP树都将SP的开销减少了至少50％。由于数据的稀疏分布，ETH数据集（图12（c））中的性能提升更为可观。

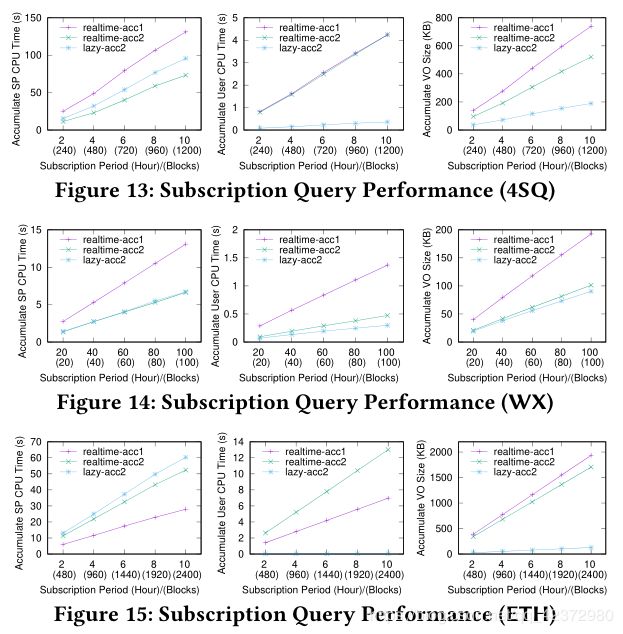
为了比较实时身份验证和惰性身份验证，我们考虑了两种实时方案（使用acc1和acc2）和一种惰性方案（仅使用acc2，因为acc1不支持累积集和证明的汇总）。对于4SQ和ETH，我们将订阅时间从2小时更改为10小时，而对于WX，我们将订阅时间更改为20小时至100小时。无花果图13-15显示了更改订阅期的结果。显然，就用户CPU时间而言，惰性方案的性能要比实时方案好得多。此外，懒惰方案中的CPU时间和VO大小仅随着订阅期的增加而呈亚线性增加。这是因为惰性方案可以跨块聚集对象不匹配的证明。相反，实时方案在新块到达时立即计算所有证明，从而导致性能变差。就SP CPU时间而言，由于惰性方案需要牺牲SP的计算来汇总不匹配证明，因此在使用相同的累加器时，其性能通常比实时方案差。

10 CONCLUSION

在本文中，我们首次在文献中研究了区块链数据库上可验证查询处理的问题。我们提出了vChain框架，以确保轻量级用户的布​​尔范围查询的完整性。我们开发了一种新颖的基于累加器的ADS方案，该方案将数值属性转换为集值属性，从而实现了对任意查询属性的动态聚合。基于此，设计了两个数据索引，即基于树的块内索引和基于跳过列表的块间索引，以及一个用于订阅查询的基于前缀树的索引，并进行了一系列优化。虽然我们提出的框架已被证明是切实可行的，但通过安全性分析和经验结果证实了所提出技术的鲁棒性。

本文为区块链研究开辟了新的方向。有许多有趣的研究问题值得进一步研究，例如，如何支持更复杂的分析查询；如何利用多核和多核等现代硬件来扩展性能；以及如何解决查询处理中的隐私问题。