(二)pytorch学习笔记 torch.nn 神经网络实现回归

来源于pytorch的官方学习资料的总结

y = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
x = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]

现在我们有十个点，横纵坐标如上所示，点的在坐标中的分布如下图所示。我们可以通过torch.nn来实现一个简单的线性回归。也就是 y = ax + b，回归的结果如图2所示。代码在最下方。


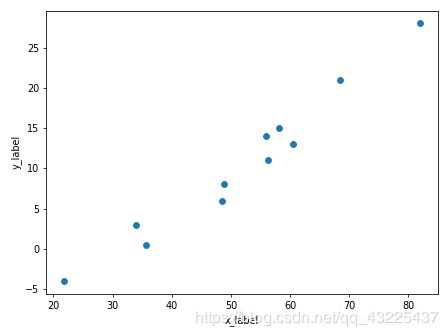
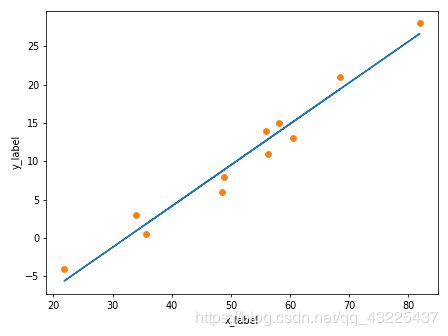
通过线性的回归我们可以得到一个可以接受的结果，但是这并不是最好的结果，我们可以通过加入激活函数来使得最后的结果变成一个曲线，去更好的拟合这些点。

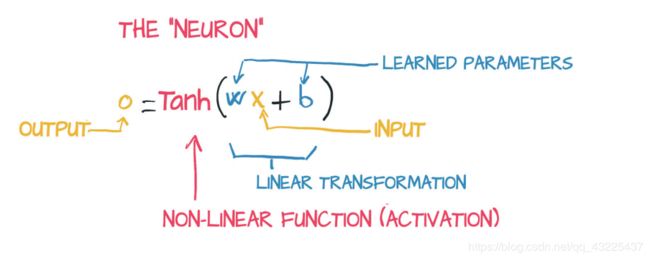
如上图，我们在（ax+b）输出的结果中加入一个激活函数，如tanh。这样出来的结果就是一个非线性的了，但是我们仅仅通过两个参数 a 和 b，是很难描绘出我们需要的曲线的。这时候我们就需要很多个像上面<<>这样的式子，去表达我们的曲线。而一个这个样的式子，就是我们的一个神经元，很多个神经元组成一个神经网络。

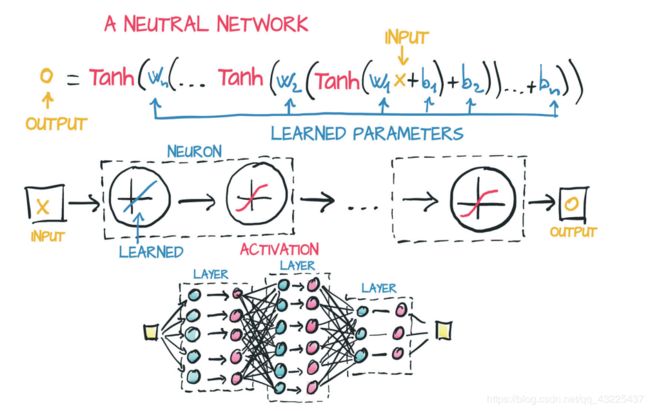
这时我们就可以通过更新整个神经网络中的权值和偏置值，来得到最终的曲线，如下图所示。

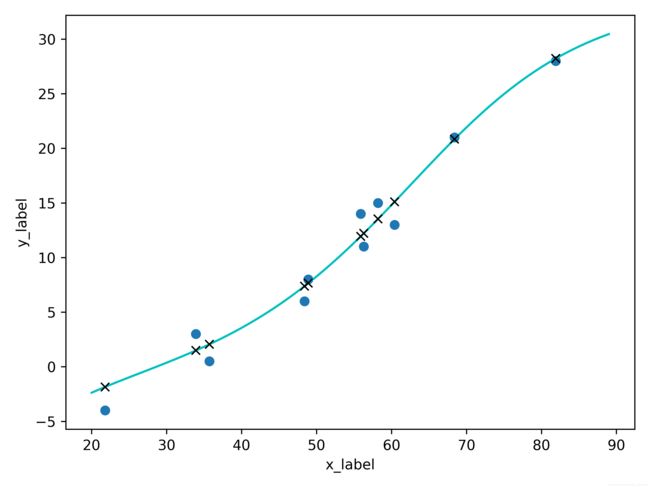
完整代码如下：

import torch.nn as nn
import torch
import numpy as np
from matplotlib import pyplot as plt
import torch.optim as optim
from collections import OrderedDict

t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]

t_c = torch.tensor(t_c).unsqueeze(1)
t_u = torch.tensor(t_u).unsqueeze(1)  # [11,1]

n_samples = t_u.shape[0]
n_val = int(0.2*n_samples)

shuffled_indices = torch.randperm(n_samples)

train_indices = shuffled_indices[:-n_val]
val_indeices = shuffled_indices[-n_val]

train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]

val_t_u = t_u[val_indeices]

val_t_c = t_c[val_indeices]

train_t_un = 0.1 * train_t_u
val_t_un = 0.1 * val_t_u


def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val, t_c_train, t_c_val):
    for epoch in range(1, n_epochs+1):
        t_p_train = model(t_u_train)
        loss_train = loss_fn(t_p_train, t_c_train)

        t_p_val = model(t_u_val)
        loss_val = loss_fn(t_p_val, t_c_val)

        optimizer.zero_grad()
        loss_train.backward()
        optimizer.step()

        if epoch == 1 or epoch % 1000 ==0 :
            print('Epoch {}, Training loss {}, Validation loss {}'.format(
                epoch, float(loss_train), float(loss_val)
            ))


linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)
print('+++++++++ linear +++++++++')
training_loop(
    n_epochs=3000,
    optimizer=optimizer,
    model=linear_model,
    loss_fn=nn.MSELoss(),
    t_u_train=train_t_un,
    t_u_val=val_t_un,
    t_c_train=train_t_c,
    t_c_val=val_t_c
)

seq_model = nn.Sequential(
    nn.Linear(1, 13),
    nn.Tanh(),
    nn.Linear(13, 1))
print('+++++++++ nn +++++++++')
optimizer = optim.SGD(seq_model.parameters(), lr=1e-3)
training_loop(
    n_epochs=5000,
    optimizer=optimizer,
    model=seq_model,
    loss_fn=nn.MSELoss(),
    t_u_train=train_t_un,
    t_u_val=val_t_un,
    t_c_train=train_t_c,
    t_c_val=val_t_c
)

t_range = torch.arange(20., 90.).unsqueeze(1)
# print(t_range)
# print(seq_model(torch.from_numpy(np.array([[20.]])).float()).detach().numpy())
# exit()

fig = plt.figure(dpi=600)
plt.xlabel('x_label')
plt.ylabel('y_label')
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
plt.show()