JZOJ6021. 【GDOI2019模拟2019.2.15】车

Description

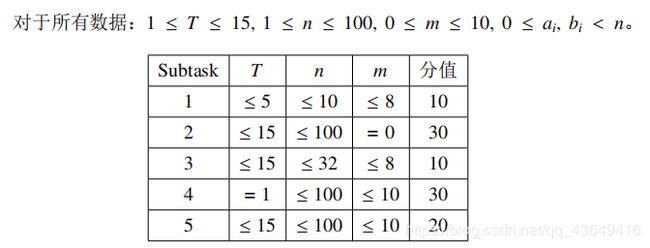
Data Constraint

Solution

• 容斥！

• 首先如果没有对角线的限制，方案显然是n!
• 容斥1：将不能放改为必须放，枚举集合，容斥系数为(-1)^size
• 容斥2：两条对角线必须有，改为总方案减去一条没有的方案加上两条没有的方案。
• 容斥3：一条对角线没有的方案，改为总方案减去有若干个的方案，容斥系数(-1)^cnt，组合数计算一下。
• 容斥4：两条对角线没有的方案，改为总方案减去两条对角线共有若干个的方案，容斥系数同上。这个需要用DP，将每一圈（每一个正方形边框）分层，然后背包计算。
• 至此时间复杂度O(T* n* n* 2^m).

#include
#include
#include
#include
#define maxn 105
#define maxm 11
#define mo 10007
using namespace std;

int T,n,m,i,j,k,bzh[maxn],bzw[maxn],b[maxm][2],map[maxn][maxn];
int jc[maxn],C[maxn][maxn],ans,f[maxn];

int doit(int res){
	int sum=jc[res],cnt=0,sum0=0,tp0=1,tp1=1;
	for(int i=0;i=0;j--) {
					if (j>=1) (f[j]+=f[j-1]*4)%=mo;
					if (j>=2) (f[j]+=f[j-2]*2)%=mo;
				} 
			if (cnt==1)
				for(int j=n;j>=1;j--) 
					(f[j]+=f[j-1]*2)%=mo;
			if (cnt==2&&bzh[i]+bzh[n-i-1]==1)
				for(int j=n;j>=1;j--)
					(f[j]+=f[j-1])%=mo;
		}
		if ((n&1)&&!bzw[n/2]&&!bzh[n/2]) 
			for(int i=n;i>=1;i--) (f[i]+=f[i-1])%=mo;
		
		sum0=0;
		for(int i=0;i<=n;i++) sum0=(sum0+((i&1)?-1:1)*f[i]*jc[res-i]%mo+mo)%mo;
		sum=(sum+sum0+mo)%mo;
	}
	return sum;
}

void dfs(int i,int ct){
	if (i>m) {ans=(ans+((ct&1)?-1:1)*doit(n-ct)+mo)%mo;return;}
	
	if (!bzh[b[i][0]]&&!bzw[b[i][1]]){
		bzh[b[i][0]]=bzw[b[i][1]]=1;
		map[b[i][0]][b[i][1]]=1;
		dfs(i+1,ct+1);
		bzh[b[i][0]]=bzw[b[i][1]]=0;
		map[b[i][0]][b[i][1]]=0;
	}
	dfs(i+1,ct);
}

int main(){
	freopen("rook.in","r",stdin);
	freopen("rook.out","w",stdout);
	scanf("%d",&T);
	while (T--){
		scanf("%d%d",&n,&m);
		for(i=1;i<=m;i++) scanf("%d%d",&b[i][0],&b[i][1]);
		
		jc[0]=1; for(i=1;i<=n;i++) jc[i]=jc[i-1]*i%mo;
		C[0][0]=1;
		for(i=1;i<=n;i++){
			C[i][0]=1;
			for(j=1;j<=i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mo;
		}
		
		ans=0;
		dfs(1,0);
		printf("%d\n",ans);
	}
}