Delta机器人的运动学分析

Delta机器人的运动学分析

@(1@Personal)[DeltaRobot,BLOG]

暂时放出位置分析，稍后更新速度及加加速度分析。

---

约定

机构简述

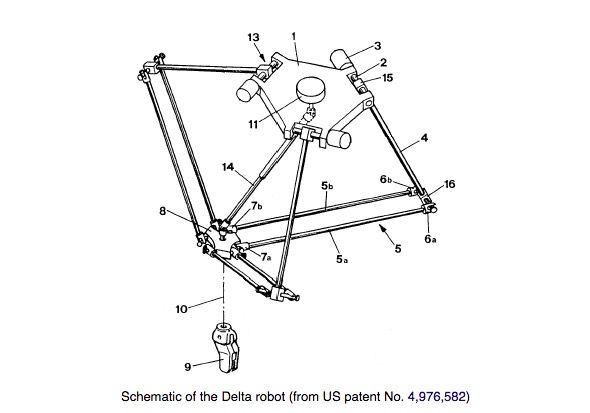
The delta robot consists of two platforms: the upper one (1) with three motors (3) mounted on it, and smaller one (8) with an end effector (9). The platforms are connected through three arms with parallelograms, the parallelograms restrain the orientation of the lower platform to be parallel to the working surface (table, conveyor belt and so on). The motors (3) set the position of the arms (4) and, thereby, the XYZ-position of the end effector, while the fourth motor (11) is used for rotation of the end effector. You can find more detailed description of delta robot design in the corresponding Wikipedia article.

参数

名称	意义
b	基座中心到电机的距离
a	主动臂长度
f	从动臂长度
p	移动平台中心到链接点的距离
E1、2、3	肘关节
{B}	基座所在平面
B0	移动平台中心位置
B1、2、3	电机位置
{P}	移动平台所在平面
P0	移动平台中心位置
P1、2、3	从动臂和移动平台连接点

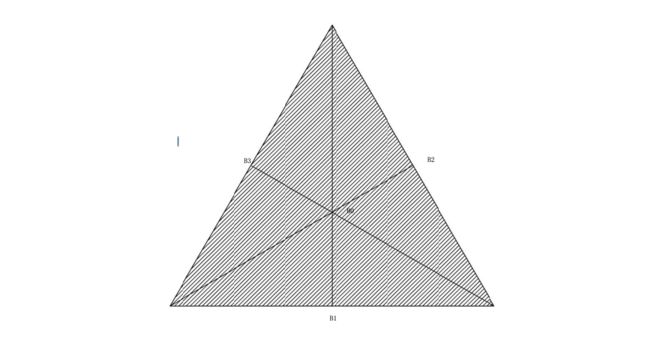
机构坐标系

机构坐标系是一个笛卡尔坐标系统，原点与 B0 重合，且 B1 在y轴上，xy平面与 {B} 重合。

轴坐标系

顺时针旋转为角度正方向。

---

前期分析

假设 P0 坐标为 (x,y,z) ;三轴转角为 (θ1,θ2,θ3) 。

约束环

为方便理解，Delta机器人的机械结构可以解耦成3个独立的运动学约束环。下图是以1轴为基准的约束环：

{B0P1}={B0B1}+{B1E1}+{E1P1}={B0P0}+{P0P1}

这里需要注意，由于Delta结构的特性， {B1E1} 在yz平面上， {P0P1} 平衡于y轴。

为求解方便，将等式 (???) 变换为 {E1P1} 的表达式：

{E1P1}={B0P0}+{P0P1}−{B0B1}−{B1E1}

其中：

{B0P0}=⎧⎩⎨⎪⎪xyz⎫⎭⎬⎪⎪

{P0P1}=⎧⎩⎨⎪⎪0−p0⎫⎭⎬⎪⎪

{B0B1}=⎧⎩⎨⎪⎪0−b0⎫⎭⎬⎪⎪

{B1E1}=⎧⎩⎨⎪⎪0−acosθ1−asinθ1⎫⎭⎬⎪⎪

将等式 (???) 、 (???) 、 (???) 和 (???) 代入 (???) 得：

{E1P1}=⎧⎩⎨⎪⎪xyz⎫⎭⎬⎪⎪+⎧⎩⎨⎪⎪0acosθ1+b−pasinθ1⎫⎭⎬⎪⎪

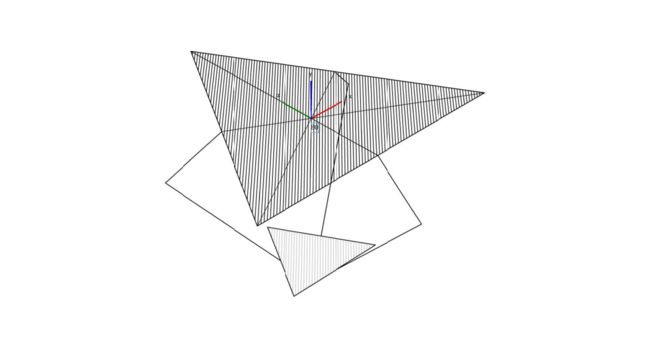
三个约束环的关系

如图所示，三个约束环在空间坐标内绕Z轴旋转，相互形成120度的夹角。那么，以1轴为基准的各约束环坐标变换矩阵如下。

[Ri]=⎡⎣⎢cosαi−sinαi0sinαicosαi0001⎤⎦⎥i=1,2,3其中：⎧⎩⎨⎪⎪α1=0α2=120α3=240

推广

现在将等式 (???) 推广为3个约束环通式：

{EiPi}=⎧⎩⎨⎪⎪xyz⎫⎭⎬⎪⎪+[Ri]⎧⎩⎨⎪⎪0acosθ1+b−pasinθ1⎫⎭⎬⎪⎪i=1,2,3

展开

由于 {EiPi} 的模为 f ，得等式：

∥∥{EiPi}∥∥2=f2i=1,2,3

将等式 (???) 代入等式 (???) 得到约束环方程组：

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪2a(y+A)cosθ1+2zasinθ1+x2+y2+z2+A2+a2+2yA−f2=0−a(3√(x+B)+y+C)cosθ2+2zasinθ2+x2+y2+z2+B2+C2+a2+2xB+2yC−f2=0a(3√(x−B)−y−C)cosθ3+2zasinθ3+x2+y2+z2+B2+C2+a2−2xB+2yC−f2=0其中：⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪A=b−pB=3√2(p−b)C=12(p−b)

---

反向位置运动学分析

为求解方便，将方程组 (???) 转化成以下形式：

Gicosθi+Hisinθi+Ii=0i=1,2,3其中:⎧⎩⎨⎪⎪G1=2a(y+A)H1=2zaI1=x2+y2+z2+A2+a2+2yA−f2⎧⎩⎨⎪⎪G2=−a(3√(x+B)+y+C)H2=2zaI2=x2+y2+z2+B2+C2+a2+2(xB+yC)−f2⎧⎩⎨⎪⎪G3=a(3√(x−B)−y−C)H3=2zaI3=x2+y2+z2+B2+C2+a2+2(−xB+yC)−f2

运用半角公式，定义 ti=tanθi2i=1,2,3 ，并将其代入等式 (???) :

Gi(1−t2i)+Hi(2ti)+Ii(1+t2i)=0i=1,2,3

然后解得：

ti=−Hi±G2i+H2i−I2i−−−−−−−−−−−√Ii−Gi

最后解得：

θi=2tan−1(ti)

这时候每个约束环可以解出两个角度，三个电机合起来有八组解。一般情况下我们只选择所有机器臂向外的那一组解。

---