Semantic Autoencoder for Zero-Shot learning阅读笔记CVPR2017收录

论文地址：https://arxiv.org/pdf/1704.08345.pdf

代码地址：https://elyorcv.github.io/projects/sae

该论文已经被CVPR2017收录。主要是关于利用语义自编码器实现zero-shot learning的工作。一定程度上解决了训练集和测试集的领域漂移（domain shift）问题。整个算法最核心的地方是在自编码器进行编码和解码时，使用了原始数据作为约束，即编码后的数据能够尽可能恢复为原来的数据。该方法在6个数据集上的zero-shot learning结果都为目前最好。该方法还能解决监督聚类问题（supervised clustering problem），并也能取得目前最好的效果。

作者使用了一个十分基础的自编码器对原始样本进行编码，其结构如图1所示，其中X为样本，S为自编码器的隐层，x^为由隐层还原为样本的表示。需要注意的是隐藏层S层为属性层，它不仅仅是原样本的另一种表示，它同时也有着清晰的语义。

图1 自编码器结构

贡献
（1）提出了一种新的用于zero-shot learning语义自编码模型；（2）提出了模型对应的高效的学习算法；（3）算法具有扩展性，可以用于监督聚类问题（supervised clustering问题）。实验证明，该算法在多个数据集上能取得最好效果。

映射领域漂移（Projection domain shift）
对于zero-shot learning问题，由于训练模型时，对于测试数据类别是不可见的，因此，当训练集和测试集的类别相差很大的时候，比如一个里面全是动物，另一个全是家具，在这种情况下，传统zero-shot learning的效果将受到很大的影响。

算法内容
语义自编码器
上文已经提到了作者所使用的自编码器，它只有一层隐层，且隐层的维数要小于输入层的维度。设输入层到隐层的映射为W，隐层到输出层的映射为W*，W和W*是对称的，即有W*等于W的转置。由于我们希望输入和输出尽可能相似，则可设目标函数为：

传统的自编码器是非监督学习的，但在此问题中，我们希望中间层能够有语义的含义，能表示类标或者表示样本属性。即，加入约束WX=S，其中S是X对应的事先定义好的语义向量，换句话说，每个样本x都可以表示为一个向量s，这个s是事先定义好的。当加入这样一个约束之后，就可以使得原本非监督学习的自编码器变为监督学习的自编码器，使得自编码器的中间层表示在合理的空间内。此时目标函数可以表示为：

目标函数最优化求解

原目标函数可以表示为：

目标函数中，有WX=S，直接使用这样的约束太强了，可以想象，需要自编码器的中间层完全等于事先定义好的值，这样的条件实在是太苛刻了。因此，可以将原式写成：

这样同时将约束写入了目标函数中，也不需要拉格朗日法进行求解了，只需要简单的步骤就可以进行求解。我们注意到上式是个标准二次型（standard quadratic formulation）的形式，利用矩阵迹的运算进行改写（Tr(X)=Tr(X转置)，Tr(W转置乘S)=Tr(S转置W)）

直接求导，让导等于0，可得：

这个式子可以写成Sylvester equation的形式，可以使用Bartels-Stewart算法[1]进行求解。在matlab中有现成的函数，代码如图2所示。最终就可以求得映射函数W。

图2 matlab代码

Zero-shot learning
有了求映射矩阵W的方法，即可以将样本映射到对应的属性空间中，即可预测测试样本的类别。如果读者很清楚zero-shot learning的概念和基本方法的话，就应该很容易理解了，为了照顾新手，这里还是说一些具体实现。在实现zero-shot learning时，我们先将数据集分为训练集和测试集，且两个数据集的数据类别之间是没有交集的。利用一些先验知识得到每种类别的属性向量表示，通过上文的方法，利用训练集训练出映射矩阵W，这样就可以对测试集中的样本进行类别的预测。

在此工作中，需要检验两个方面，一个是中间层的准确度，第二是输出层的准确度。只需要利用映射矩阵W得到测试样本的中间层表示和输出表示，与ground truth进行比较，就可以了。

如果我们抛开自编码器的结构，将问题考虑为普通的学习映射矩阵的问题，即：输入为X，属性层为S，希望学习一个映射W，使得S=WX。一般的想法就是构建如下目标函数，并且加入L2-norm作为约束。

在论文[2]中，希望能够使得属性层S能够映射回样本X，则有

可以看出，本文算法的目标函数是上述两种方法的结合，只是去除了L2-norm项。因为本文算法中隐式包含了这个约束，能够控制它的值处于一个较为合理的范围。

监督聚类（supervised clustering）
简单来说就是通过训练集训练出映射W，利用W将测试集的样本表示为属性层的表示形式，注意这里的属性层是二值化的，并且将其表示为one-hot的形式，这样就可以用属性层来表示类别了。之后再进行kmeans聚类，得到测试集合的聚类结果。

实验结果
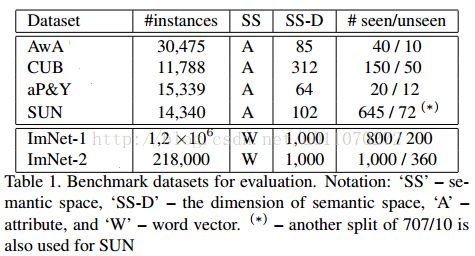
数据集：使用了6个数据集供检测算法的zero-shot learning能力，分为是：1)Animals with Attributes(AwA).2)CUB-200-2011 Birds(CUB).3)aPascal&Yahoo(aP&Y).4)SUN Attribute(SUN).5)ILSVRC2010(ImNet-1).6)ILSVRC012/ILSVRC2010(ImNet-2)。其中，后两个数据集是大型的数据集。细节如表1所示。

属性层：对于前面四个小型数据集，zero-shot learning中用到的中间属性层有数据集提供；对于大型数据集，通过训练Wikipedia语料库进行生成。
样本特征：ImNet-1使用AlexNet得到4096维特征，其他数据集样本使用GoogleNet得到样本的1024维特征。

如表2所示，为本文算法与其他算法在不同数据集上的比较结果。其中A表示属性表示，W表示词向量表示。可以看到本文算法的效果最好。

如表3所示，本文算法目标函数中两个部分共同存在的重要性，当两部分同时存在，即对映射函数增加了“可以恢复到原样本”的约束。由表可知，这个约束对结果的提升非常大。

为了进一步检测其zero-shot learning性能，作者将测试集中也包括了部分训练集的类别，这本质上是一种检测算法泛化能力的方法。结果如表4所示，可以看到在数据集AwA上要比目前最好的算法差一点点，在CUB上效果为最好。

作者还比较了算法的计算时间，由于本文算法的结构十分简单，相比之下其他算法要复杂得多，因此本文算法速度快很多。如表5所示。

作者还进行了监督聚类（supervised clustering）的检测。结果如表6、7、8和图3所示。

总结
细想来，本文提出的算法思路简单、模型简单、实现简单，但是却能达到目前最好的效果，实在令人佩服。其实，此算法最大的亮点就在于由自编码器结构所形成的对目标函数的约束，这个约束的效果非常明显。其实这个想法在论文[3]中就有体现（感兴趣的可参考http://blog.csdn.net/u011070272/article/details/73293740），其中的linguist prior思想和本文思想如出一辙，不过本文的模型要简单很多。

参考文献：

[1]Solution of the matrix equation ax+ xb= c

[2]Ridge regression, hubness, and zero-shot learning. 

[3]Automatic Discovery, Association Estimation and Learning of Semantic Attributes for a Thousand Categories