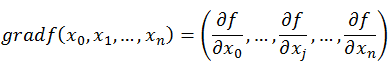机器学习——MP神经元、感知机网络、梯度下降
参考文章:
一看就懂的感知机算法PLA(基础概念)
感知机 PLA(Perceptron Learning Algorithm)(加深理解)
McCulloch and Pitts 神经元
基本原理如下图:
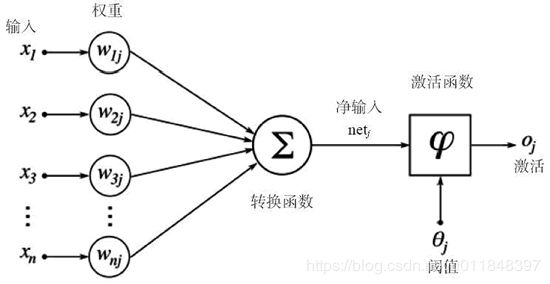
由McCulloch和Pitts于1943年发表,简单模拟了神经元的反应流程,包括:
- 多个带有权重的输入 w i × x i w_i×x_i wi×xi,相当于「突触」
- x i x_i xi是输入值,表示外界的刺激。
- w i w_i wi表示权重,表示刺激的不同强度。
- 一个转换函数 ∑ \sum ∑,相当于「汇聚电信号的细胞膜」
- ∑ x = i n w i x i \sum_{x=i}^nw_ix_i ∑x=inwixi也就是对所有带权重的输入进行简单的求和,将多个值合并为1个值。
- 一个阈值(threshold) θ \theta θ,也称激活函数,决定了外界刺激要达到什么程度神经元才会被激活
- 当刺激大于阈值 θ \theta θ时,神经被激活;否则没有。
根据以上信息我们可以得到一个基本的神经元表示(也即是分类公式):
线 性 求 和 : h = ∑ x = i n w i x i 阈 值 比 较 : y = g ( h ) { 1 i f h ≥ θ 0 i f h < θ \begin{array}{l}线性求和:h=\sum_{x=i}^nw_ix_i\\\\阈值比较:y=g(h)\;\left\{\begin{array}{l}1\;\;\;\;if\;h\geq\theta\\0\;\;\;\;if\;h<\theta\end{array}\right.\end{array} 线性求和:h=∑x=inwixi阈值比较:y=g(h){1ifh≥θ0ifh<θ
由线性相加和阈值比较两个过程组成,最后根据比较结果将样本划分为正负两类。
训练感知机 Perceptron
即使是单层感知机,也可以可以由多个相互独立的MP神经元组成(对于每个神经元,只有输入值是相同的,其他都不同,包括输入值对应的各个权重 w i w_i wi)
训练公式:
w i j ( n e w ) = w i j ( o l d ) − η ( y j − t j ) × x i w_{ij}(new)=w_{ij}(old)-\eta(y_j-t_j)×x_i wij(new)=wij(old)−η(yj−tj)×xi
公式的推导过程:
- 这里权值变为 w i j w_{ij} wij, i i i表示输入的索引, j j j表示神经元的索引
- 因为感知机有多个神经元,所以我们也将得到相同数量的输出,比如5个神经元输出集合 y = ( 1 , 1 , 1 , 0 , 1 ) y=(1,1,1,0,1) y=(1,1,1,0,1)。
- 因为是监督学习,我们还有一个正确的结果集 t = ( 1 , 1 , 1 , 1 , 0 ) t=(1,1,1,1,0) t=(1,1,1,1,0),两者比较就能够发现出错的神经元(这里是 y 4 , y 5 y_4,y_5 y4,y5出错)。
- 对于出错的神经元 k k k,我们需要改变它的权重 w i k w_{ik} wik(也就是算法学习的过程)
- 首先我们要找到要修改的权重:通过对比输出集 y y y和正确的结果集 t t t(步骤2&3),找到出错的神经元 k k k后,就能知道该神经元的所有权重 w i k w_{ik} wik都需要修改。
- 然后要判断该权重应该增大还是减小:通过「输出值」减去「正确值」 y k − t k y_k-t_k yk−tk,将得到 1 或 − 1 1或-1 1或−1。当结果为 1 1 1时,说明输出太大, w i k w_{ik} wik要减小;反之 w i k w_{ik} wik要增大。此时 w i j ( n e w ) = w i j ( o l d ) − ( y j − t j ) w_{ij}(new)=w_{ij}(old)-(y_j-t_j) wij(new)=wij(old)−(yj−tj)
- 但我们还要决定权重每次变化的程度,于是引入一个新的系数 η \eta η,表示学习速率(learning rate)。于是公式变成 w i j ( n e w ) = w i j ( o l d ) − η ( y j − t j ) w_{ij}(new)=w_{ij}(old)-\eta(y_j-t_j) wij(new)=wij(old)−η(yj−tj)
- 现在还有一个问题:并非所有的输入值都是正数。在步骤42中,我们希望通过使权值 w w w减小,进而使该神经元中的每个 w x wx wx都减小。但假如输入中存在负数,那么当权值 w w w减小时, w x 负 wx_负 wx负反而会增大。因此考虑了 x x x的符号后,得到最终公式 w i j ( n e w ) = w i j ( o l d ) − η ( y j − t j ) x i w_{ij}(new)=w_{ij}(old)-\eta(y_j-t_j)x_i wij(new)=wij(old)−η(yj−tj)xi。(关于为什么是 x i x_i xi,可看下面的梯度下降)
- 学习速率 η \eta η是手动输入的,建议取值范围是<0.1,0.4>,太高会导致每当有错误的适合都进行太大的改变,导致感知机网络始终无法稳定下来;而数值太低,则会延长计算时间。
- 在感知机网络学习正确模型的过程中,除了考虑修改权重 w w w,我们还需要考虑修改阈值 θ \theta θ。即,当所有输入都是0的时候,我们只能通过阈值的变化来改变分类结果
- 在最开始的神经元的表达式中,将「线性求和」和「阈值比较」合并,得到其中的公式部分 y = ∑ x = i n w i x i − θ y=\sum_{x=i}^nw_ix_i-\theta y=∑x=inwixi−θ
- 可将 θ \theta θ视为 w 0 w_0 w0,而对应的 x 0 x_0 x0则被固定为 − 1 -1 −1(实际上 x 0 x_0 x0可以是任何非0的值,但一旦确定就不能改变,-1可能是最常见的取值)。 x 0 x_0 x0也被称为偏移节点(bias node)或偏移输入。
(单层)感知机算法 Perceptron Learning Algorithm
-
初始化所有权重 w i j w_{ij} wij为较小的随机数(包括正负),给定一个 x 0 x_0 x0的值(比如 − 1 -1 −1)
-
训练 Training
- 进行T次迭代,或者直到所有输出都正确
- 对于每一个输入向量(输入值)
-
计算每一个神经元的输出值 y j y_j yj,最终得到一个输出集合 y y y
y = g ( ∑ x = 0 m w i x i ) = { 1 , i f ∑ x = 0 m w i j x i > 0 0 , i f ∑ x = 0 m w i j x i ≤ 0 \begin{array}{l}y=g(\sum_{x=0}^mw_ix_i)\;=\left\{\begin{array}{l}1,\;\;\;\;if\;\;\;\sum_{x=0}^mw_{ij}x_i>0\\0,\;\;\;\;if\;\;\;\sum_{x=0}^mw_{ij}x_i\leq0\end{array}\right.\end{array} y=g(∑x=0mwixi)={1,if∑x=0mwijxi>00,if∑x=0mwijxi≤0 -
更新每一个错误的权重值 w i j w_{ij} wij
w i j ( n e w ) = w i j ( o l d ) − η ( y j − k j ) × x i w_{ij}(new)=w_{ij}(old)-\eta(y_j-k_j)×x_i wij(new)=wij(old)−η(yj−kj)×xi
-
- 对于每一个输入向量(输入值)
- 进行T次迭代,或者直到所有输出都正确
梯度下降 Gradient descent 和感知机
引用:
机器学习(一)-感知机
机器学习之感知机与梯度下降法认知
最终公式:
w t + 1 = w t − η 1 N ∑ x n ∈ X x n ( y n − t n ) w_{t+1}=w_t-\eta\frac{1}{N}\sum_{x_n\in X}x_n(y_n-t_n) wt+1=wt−ηN1xn∈X∑xn(yn−tn)
其中 η \eta η是步长, N N N是错误样本总数,此时表示为批量梯度下降算法。如果 N N N取1时,则为随机梯度下降算法
梯度下降和感知机
在实际问题中,并不是所有的数据都能线性可分,而我们要做到的是力求寻找到最优的超平面 S 使数据误分类点尽量最少,即损失函数最小化。
又因为误分类点个数与感知机的w和b参数均其不可导,为了引入梯度下降法求取损失函数极小值,损失函数是误分类点到超平面的总距离。
首先,根据平面外任意点 X 0 X_0 X0到超平面的距离公式 d = ∣ W X 0 + b ∣ ∣ ∣ W ∣ ∣ 2 d=\frac{|WX_0+b|}{||W||_2} d=∣∣W∣∣2∣WX0+b∣,每个划分错误的点到超平面的距离:
d e r r = ∣ W X + b ∣ ∣ ∣ w ∣ ∣ = ∣ ( y − t ) ( w x ) ∣ ∣ ∣ w ∣ ∣ d_{err}=\frac{|WX+b|}{||w||}=\frac{|(y-t)(wx)|}{||w||} derr=∣∣w∣∣∣WX+b∣=∣∣w∣∣∣(y−t)(wx)∣
其中 y y y是输出, t t t是正确结果。
对于所有错误的点,如果 w x > 0 wx>0 wx>0,则输出值 y = 1 y=1 y=1,因为是错误点,正确的结果与输出值不一致,因此 t = 0 t=0 t=0,相减得到 y − t > 0 y-t>0 y−t>0。所以 ( y − t ) ( w x ) > 0 (y-t)(wx)>0 (y−t)(wx)>0;反之, w x < 0 wx<0 wx<0, y − t < 0 y-t<0 y−t<0,所以 ( y − t ) ( w x ) > 0 (y-t)(wx)>0 (y−t)(wx)>0同样成立。
又因为 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣不存在方向,不影响后续使用梯度下降法求最优解,因此省去,以便计算
根据以上前提,可以进一步得到所有错误点到超平面的比例距离(非实际距离,而是省去了 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣)公式:
E p ( X ) = ∑ d e r r = ∑ x n ∈ X w x n ( y n − t n ) E_p(X)=\sum d_{err}=\sum_{x_n\in X}wx_n(y_n-t_n) Ep(X)=∑derr=xn∈X∑wxn(yn−tn)
这里 E p ( X ) E_p(X) Ep(X)表示:p=perceptron, E=error points, X=all points
下一步,通过梯度下降对该函数求最优解,即求该函数关于 w w w的偏导数(因为 x x x是固定值,要得到的是下一个 w w w,使得总体错误距离最更小),将上公式求偏导 ∇ E p ( X ) = ∑ x n ∈ X x n ( y n − t n ) \nabla E_p(X)=\sum_{x_n\in X}x_n(y_n-t_n) ∇Ep(X)=xn∈X∑xn(yn−tn)然后代入梯度下降公式:
x t + 1 = x t − η ∇ f ( x t ) x_{t+1}=x_t-\eta\nabla f(x_t) xt+1=xt−η∇f(xt)
其中, x t x_t xt是自变量参数向量,即当前坐标, η η η是学习因子,即下山每次前进的一小步(步进长度), x t + 1 x_{t+1} xt+1是下一步,即下山移动一小步之后的位置。
∇ f ( x ) \nabla f(x) ∇f(x)则代表着梯度,也就是函数的偏导数集合构成的向量
最后得到: w t + 1 = w t − η ∑ x n ∈ X x n ( y n − t n ) w_{t+1}=w_t-\eta\sum_{x_n\in X}x_n(y_n-t_n) wt+1=wt−ηxn∈X∑xn(yn−tn)也就是感知机训练公式,可用于无法直接进行线性二分的数据集
相关公式和概念:
- 超平面公式: W X + b = 0 WX+b=0 WX+b=0,其中 W W W是超平面的法向量, ∣ X ∣ |X| ∣X∣表示超平面上任意点的坐标向量
- 梯度下降算法: x t + 1 = x t − η ⋅ ∇ f ( x t ) x_{t+1}=x_t-\eta⋅\nabla f(x_t) xt+1=xt−η⋅∇f(xt)
- 平面外点 X 0 X_0 X0到超平面的距离公式: d = ∣ W X 0 + b ∣ ∣ ∣ W ∣ ∣ 2 d=\frac{|WX_0+b|}{||W||_2} d=∣∣W∣∣2∣WX0+b∣,其中 ∣ ∣ W ∣ ∣ 2 ||W||_2 ∣∣W∣∣2是2-范数norm,即欧几里得范数(平方求和再开方),也就是向量的模,也即是向量的大小
什么是梯度
梯度即函数在某一点最大的方向导数,函数沿梯度方向函数有最大的变化率。
- 梯度是偏导数的集合
- 导数是指一元函数上某一点的斜率
- 偏导数是指,多元函数中,函数在某一点处沿某一坐标轴正方向的变化率
- 方向导数是指,多元函数某一点在沿某一任意方向上的导数值
- 一个多元函数的偏导数集合构成的向量,是该函数的最大方向向量
梯度下降算法
x t + 1 = x t − η ⋅ ∇ f ( x t ) x_{t+1}=x_t-\eta⋅\nabla f(x_t) xt+1=xt−η⋅∇f(xt)
其中, x t x_t xt是自变量参数向量,即当前坐标, η η η是学习因子,即下山每次前进的一小步(步进长度), x t + 1 x_{t+1} xt+1是下一步,即下山移动一小步之后的位置。
∇ f ( x ) \nabla f(x) ∇f(x)则代表着梯度,也就是函数的偏导数集合构成的向量
梯度下降的种类:
参考文章
- 批量(batch)梯度下降:每次更新使用所有样本。适用于样本不多的情况
- 优点:可以得到全局最优
- 缺点:耗时大
- 随机梯度下降:每次更新随机选择一个点。
- 优点:速度快,更快收敛。
- 缺点:不是每次迭代得到的损失函数都向着全局最优方向(但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近)
- mini-batch 梯度下降:属于折中方案,用一些小样本来近似全部的样本