小瓜讲机器学习——分类算法（二）支持向量机（SVM）算法原理详解

2.支持向量机(SVM)算法原理

还以逻辑回归分类算法中图1.1的二分类问题为例，大家肯定发现了其实超平面存在很多个超平面，都能把十字点和⚪点分隔开，如下图。

超平面${\Omega }_1$、${\Omega }_2$、${\Omega }_3$…都能将图中的点分割开，那么${\Omega }_1$、${\Omega }_2$、${\Omega }_3$…到底有啥不一样的呢？他们的分割的效果一样好吗？是不是存在一个分割效果最好的超平面呢？答案是肯定的，那就是支持向量机能够回答的。

2.1 感知机模型

对于上图中的二分类，我们定义十字点为正实例z=+1，⚪点为负实例z=-1，那么就是建立了某种映射，如下所示
$$\{图中十字点+⚪点\}\Rightarrow Z=\{\begin{array}{l}+1\\ -1\end{array}$$
那么如果存在一个可以分割的超平面$\{\Omega :\sum {\omega }_i{X}_i+b=0\}$，那么上述映射关系可以转化为映射函数$f(x)$
$$z=f(X_i)=sign(\sum {\omega }_i{X}_i+b)=\{\begin{array}{ll}+1,& 在超平面上方\\ 0,& 在超平面上\\ -1,& 在超平面下方\end{array}$$
观察到对于每一个误分类，都有$-z^{(i)}\times (\sum {\omega }_i{X}_i+b)>0$ (即异号)，那么这个分割超平面应该使误分类的可能性最小，即
$$({\omega }_i,b)\to \underset{({\omega }_i,b)}{\min }J({\omega }_i,b)=\underset{({\omega }_i,b)}{\min }[-\sum _{i\in M}{z}^{(i)}\times (\sum {\omega }_i{X}_i+b)]$$
其中M为误分类集合。
求解该极值问题，就能够确定一组$({\omega }_i,b)$。这种分类算法叫感知机算法。

2.2 函数间隔和几何间隔

函数间隔
对于给定的m个样本点$\{(X_i^{(1)},z^{(1)}),(X_i^{(2)},z^{(2)}),...,(X_i^{(m)},z^{(m)})\}$,假设存在分割超平面$\{\Omega :\sum {\omega }_i{X}_i+b=0\}$，那么每一个样本点$\sum {\omega }_i{X}_i+b$ 值不仅能够表明是在超平面上还是下（如果大于0，在上，小于0，在下），还能一定程度上表明距离超平面的远近，为了避免正负的麻烦，我们定义函数间隔为
$${\hat{\gamma }}_i=z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)$$
那么距离给定超平面最近的样本点就可以用最小函数间隔来等效。
$$\hat{\gamma }=\underset{i=1...m}{\min }{\hat{\gamma }}_i$$
其实函数间隔可以写成如下形式
$${\hat{\gamma }}_i=z^{(k)}[({\omega }_1,...,{\omega }_n{)}^T\bullet (X_1^{(k)},...,X_n^{(k)})+b]$$
$({\omega }_1,...,{\omega }_n{)}^T$是超平面$\{\Omega :\sum {\omega }_i{X}_i+b=0\}$的法向量$N$，显然${\hat{\gamma }}_i$就是特征向量$(X_1^{(k)},...,X_n^{(k)})$在超平面法向的投影，但是由于法向量$N$没有单位化（归一化），这样定义的函数间隔存在一个问题，如果$N=({\omega }_1,...,{\omega }_n{)}^T$等比变化，实际上超平面$\{\Omega :\sum {\omega }_i{X}_i+b=0\}$是同一个，但是函数间隔却是变化的。
所以将法向量单位化（归一化），这样就定义了几何间隔。

几何间隔

定义几何间隔如下式
$${\gamma }_i=\frac{{\hat{\gamma }}_i}{||W||}=z^{(k)}\frac{(\sum {\omega }_i{X}_i^{(k)}+b)}{||W||}$$
相应的距离超平面最近的样本点与几何间隔最小等效。
$$\gamma =\underset{i=1...m}{\min }{\gamma }_i$$
其实不难发现，对于正确分类的样本点，几何间隔可以变换为
$${\gamma }_i=z^{(k)}\frac{(\sum {\omega }_i{X}_i^{(k)}+b)}{||W||}=\frac{|\sum {\omega }_i{X}_i^{(k)}+b|}{||W||}$$
学过解析几何的知识，不难发现这就是点到超平面的距离公式。

2.3 支持向量机模型

支持向量机模型就是找到一个超平面使得样本点到超平面的距离最大，也就是说对于m样本点来说，找一个超平面，使得最小几何间隔最大化（即m个样本点中离超平面最近的那个点到超平面的距离最大化）。
$$\begin{array}{rl}& ({\omega }_i,b)\to \underset{({\omega }_i,b)}{\max }\gamma =\underset{({\omega }_i,b)}{\max }\frac{\hat{\gamma }}{||W||}\\ & s.t.z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)\ge \hat{\gamma }\end{array}$$
实际上，超平面$\{\Omega :\sum {\omega }_i{X}_i+b=0\}$与$\{\Omega :\frac{\sum {\omega }_i{X}_i+b}{\hat{\gamma }}=0\}$是一样的，所以上述问题就等效为
$$\begin{array}{rl}& ({\omega }_i,b)\to \underset{({\omega }_i,b)}{\max }\gamma =\underset{({\omega }_i,b)}{\max }\frac{1}{||W||}\\ & s.t.z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)\ge 1\end{array}$$
我们不难推断$\frac{1}{||W||}$达到最大值与$\frac{||W|{|}^2}{2}$达到最小值是等价的。所以最后问题等价与
$$\begin{array}{rl}& ({\omega }_i,b)\to =\underset{({\omega }_i,b)}{\min }\frac{||W|{|}^2}{2}\\ & s.t.z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)\ge 1\end{array}$$
这个就是线性可分的支持向量机模型。

显然支持向量机模型找到的超平面一定是最靠近超平面的正实例样本点A和负实例样本点B到超平面具有相等的几何间距，并且样本点A和样本点B称为支持向量。
同时对于距离超平面最近的样本点，$z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)\ge 1$取到等号。
即对于正实例，$z^{(k)}=+1,\sum {\omega }_i{X}_i^{(k)}+b=1$
对于负实例，$z^{(k)}=-1,\sum {\omega }_i{X}_i^{(k)}+b=-1$

2.4 支持向量机模型的对偶问题

支持向量机模型转换成约束条件下最优化问题，也就是一个求解条件极值的问题，回忆大学数学，关于求解条件极值问题有一个很好的方案——拉格朗日乘子法。

2.4.1 拉格朗日乘子法

对于一个一般性的约束最优化问题①，如下
$$\begin{array}{rl}& \min f(x)\\ & s.t.g_i(x)\le 0\\ & h_i(x)=0\end{array}$$
这是一个典型的条件极值问题，其中约束条件有等式约束与不等式约束。
使用拉格朗日乘子法建立拉格朗日函数$L(x,{\alpha }_i,{\lambda }_i)$，如下
$$L(x,{\alpha }_i,{\lambda }_i)=f(x)+\sum _i{\alpha }_i{g}_i(x)+\sum _i{\lambda }_i{h}_i(x)$$
上述条件极值问题就转化成如下一般极值问题。
$$\min L(x,{\alpha }_i,{\lambda }_i)$$
对于$f(x)$是凸函数的情况下，拉格朗日函数的一般极值问题就是让一阶导数等于零即可。但是由于存在不等式约束，拉格朗日函数的一般极值问题就比较复杂。我们将原问题转化为两部分，1.等式约束，2.不等式约束。
2.4.2 KKT条件推导

等式约束

$$\begin{array}{rl}& \min f(x)\\ & s.t.h_i(x)=0\end{array}$$
这个时候拉格朗日函数$\hat{L}(x,{\lambda }_i)=f(x)+{\sum }_i{\lambda }_i{h}_i(x)$，原问题的等式约束条件下取极小值问题就转化为无约束条件下拉格朗日函数$\hat{L}(x,{\lambda }_i)$取极小值问题，即
$$\min \hat{L}(x,{\lambda }_i)$$
当取到极小值的时候，拉格朗日函数$\hat{L}(x,{\lambda }_i)$满足以下关系
$$\nabla L=0\Rightarrow \{\begin{array}{l}\frac{\partial \hat{L}}{\partial x}=\frac{\partial f(x)}{\partial x}+{\sum }_i{\lambda }_i\frac{\partial h_i(x)}{\partial x}=0\\ \frac{\partial \hat{L}}{\partial {\lambda }_i}=0\end{array}$$

不等式约束

利用等式约束的结果，原问题①就变成拉格朗日函数$\hat{L}(x,{\lambda }_i)$的不等式约束条件下取极小值问题，即
$$\begin{array}{r}\min \hat{L}(x,{\lambda }_i)\\ s.t.g_i(x)\le 0\end{array}$$
同样再次利用拉格朗日乘子法建立拉格朗日函数$L(x,{\alpha }_i,{\lambda }_i)$，即有
$$L(x,{\alpha }_i,{\lambda }_i)=\hat{L}(x,{\lambda }_i)+\sum _i{\alpha }_i{g}_i(x)=f(x)+\sum _i{\alpha }_i{g}_i(x)+\sum _i{\lambda }_i{h}_i(x)$$

定义原问题的可行域（定义域）为$\{x\in R^n|g_i(x)\le 0\}$。假设存在一个$x^{\ast }$是满足可行域的极值问题的最佳解，那么存在下式
$$\nabla L=0\Rightarrow \{\begin{array}{l}\frac{\partial L}{\partial x}=\frac{\partial \hat{L}(x^{\ast })}{\partial x}+\sum {\alpha }_i\frac{\partial g_i(x^{\ast })}{\partial x}=\frac{\partial f(x^{\ast })}{\partial x}+\sum {\lambda }_i\frac{\partial h_i(x^{\ast })}{\partial x}+\sum {\alpha }_i\frac{\partial g_i(x^{\ast })}{\partial x}=0\\ \frac{\partial \hat{L}}{\partial {\lambda }_i}=0\end{array}$$

我们讨论$x^{\ast }$，那么实际上只存在两种情况，即

1. 如果$x^{\ast }$在可行域内，即有$g_i(x)<0$，由于$\hat{L}(x,{\lambda }_i)$是凸函数，那么显然$x^{\ast }$就是全局极小值，$g_i(x)<0$实际上是冗余条件，必然可以满足，可知${\alpha }_i=0$。

2. 如果$x^{\ast }$在可行域边界，即有$g_i(x)=0$，由于$\hat{L}(x,{\lambda }_i)$是凸函数，如果$x^{\ast }$不是全局极小值，那么一定有$\hat{L}(x,{\lambda }_i)$梯度方向($\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$)指向可行域（即$\hat{L}(x,{\lambda }_i)$朝向可行域内部是增函数），由于$g_i(x)$的梯度是指向可行域以外（因为可行域内是$g_i(x)<0$，可行域以外是$g_i(x)>0$，那么在边界上指向可行域以外$g_i(x)$是增函数），如图所示。
   
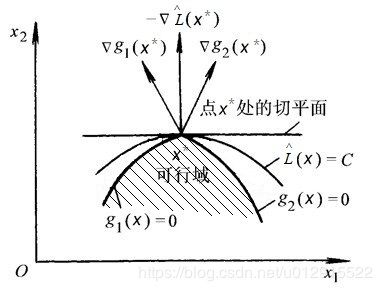
   那么现在讨论梯度方向$\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$与$\frac{\partial g_i(x)}{\partial x}$之间的关系，实际上可以得出梯度方向$\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$一定在$\frac{\partial g_i(x)}{\partial x}$组成的锥体内，否则，假设在锥体外，如下图所示，$\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$不在锥体内，假设$\frac{\partial g_i(x)}{\partial x}$都在$\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$左侧，黑色斜剖面线是$g_2(x)\le 0$，绿色斜剖面线是$g_1(x)\le 0$，红色部分即为不等式约束条件下的可行域。其中$l_{\hat{L}}$是点$X^{\ast }$处的切平面，$l_{g_i}$是点$X^{\ast }$处的$g_i$切平面，切平面$l_{\hat{L}}$与切平面$g_i$的关系如下图中所示。

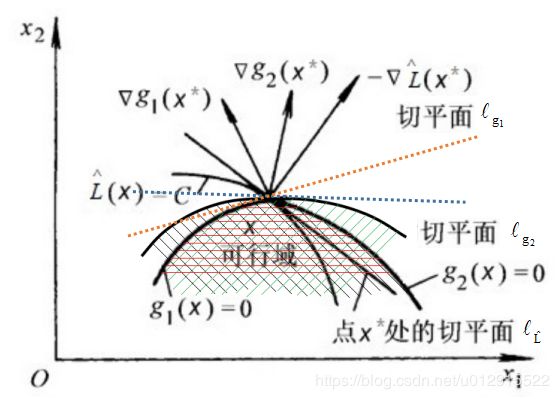
那么可行域与$L(x)$的等高线之间必然存在如下图蓝色斜剖面线的区域，而蓝色斜剖面线区域在$L(x)$减小的方向，所以在蓝色斜剖面线中$L(x)<C$，这与在$x^{\ast }$处取极小值相违背，所以$\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$不在锥体内不成立。

$$\frac{\partial \hat{L}(x^{\ast })}{\partial x}+\sum {\alpha }_i\frac{\partial g_i(x^{\ast })}{\partial x}=0\Rightarrow -\frac{\partial \hat{L}(x^{\ast })}{\partial x}=\sum {\alpha }_i\frac{\partial g_i(x^{\ast })}{\partial x}$$
由$\frac{\partial \hat{L}(x,{\lambda }_i)}{\partial x}$在锥体内成立，可得${\alpha }_i\ge 0$。

综合两种情况，必然有${\alpha }_i{h}_i(x)=0$成立。

所以原问题① 取到极小值拉格朗日函数$L(x,{\alpha }_i,{\lambda }_i)$必然满足以下关系式
$$\{\begin{array}{l}\frac{\partial L(x,{\alpha }_i,{\lambda }_i)}{\partial x}=0\\ \frac{\partial L(x,{\alpha }_i,{\lambda }_i)}{\partial {\alpha }_i}=0\\ \frac{\partial L(x,{\alpha }_i,{\lambda }_i)}{\partial {\lambda }_i}=0\\ g_i(x)\le 0\\ h_i(x)=0\\ {\alpha }_i\ge 0\\ {\alpha }_i{h}_i(x)=0\end{array}$$
这组条件就叫Karush-Kuhn-Tucker (KKT)条件。

2.4.3 拉格朗日对偶问题
（证明思路摘自《统计学习方法》附录C）
原问题的转化
对于一个一般性的约束最优化问题①，如下
$$\begin{array}{rl}& \min f(x)\\ & s.t.g_i(x)\le 0\\ & h_i(x)=0\end{array}$$
其拉格朗日函数为$L(x,{\alpha }_i,{\lambda }_i)$，即有
$$L(x,{\alpha }_i,{\lambda }_i)=\hat{L}(x,{\lambda }_i)+\sum _i{\alpha }_i{g}_i(x)=f(x)+\sum _i{\alpha }_i{g}_i(x)+\sum _i{\lambda }_i{h}_i(x)$$
定义
$${\theta }_P=\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\ge 0}{\max }[L(x,{\alpha }_i,{\lambda }_i)]$$
在可行域内，对于拉格朗日函数$L(x,{\alpha }_i,{\lambda }_i)$，必然有
$$\begin{array}{rl}L(x,{\alpha }_i,{\lambda }_i)& =f(x)+\sum _i{\alpha }_i{g}_i(x)+\sum _i{\lambda }_i{h}_i(x)\\ & \equiv f(x)\end{array}$$
故，
$${\theta }_P=\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\ge 0}{\max }[L(x,{\alpha }_i,{\lambda }_i)]=f(x)$$
在可行域外，比如$g_i(x)>0or{h}_i(x)=0$，那么${\theta }_P=+\infty$。
$${\theta }_P=\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\ge 0}{\max }[L(x,{\alpha }_i,{\lambda }_i)]=\{\begin{array}{ll}& f(x)\\ & +\infty \end{array}$$
那么原问题就转化为
$$\underset{x}{\min }\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\ge 0}{\max }[L(x,{\alpha }_i,{\lambda }_i)]$$
这样就把约束条件下的优化问题转化成无条件约束问题。

对偶问题

定义
$${\theta }_D=\underset{x}{\min }L(x,{\alpha }_i,{\lambda }_i)$$
那么
$$\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }{\theta }_D=\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }\underset{x}{\min }L(x,{\alpha }_i,{\lambda }_i)$$
为拉格朗日对偶问题，上式可写成一般形式的约束条件下的最大值问题
$$\begin{array}{rl}& \underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }{\theta }_D=\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }\underset{x}{\min }L(x,{\alpha }_i,{\lambda }_i)\\ & s.t.{\alpha }_i\le 0\end{array}$$
这是原问题的对偶问题。

原问题与对偶问题的关系
若原问题和对偶问题都存在最优解，假设$d^{\ast }$为对偶问题的最优解，$p^{\ast }$为原问题的最优解，那么
$${\theta }_D=\underset{x}{\min }L(x,{\alpha }_i,{\lambda }_i)\le L(x,{\alpha }_i,{\lambda }_i)\le \underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }L(x,{\alpha }_i,{\lambda }_i)={\theta }_P$$
$$d^{\ast }=\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }\underset{x}{\min }L(x,{\alpha }_i,{\lambda }_i)\le \underset{x}{\min }\underset{{\alpha }_i,{\lambda }_i;{\alpha }_i\le 0}{\max }L(x,{\alpha }_i,{\lambda }_i)=p^{\ast }$$
我们成这个关系为拉格朗日弱对偶性，如果等式严格成立，我们称之为拉格朗日强对偶性。
我们不加证明的引入以下引理（Slater条件）
引理：当原问题为凸优化问题，且存在严格满足不等式约束条件的$x$，那么存在一组$(x^{\ast },{\alpha }_i^{\ast },{\lambda }_i^{\ast })$是原问题的最优解，也是对偶问题的最优解，且满足强对偶性$d^{\ast }=p^{\ast }=L(x^{\ast },{\alpha }_i^{\ast },{\lambda }_i^{\ast })$。

对偶问题的KKT条件
在满足强对偶性的条件下，求解原问题可以转化求解对偶问题，由于原问题约束复杂，相对来说对偶问题会比较好求解。当然原问题取到极值的kkt条件在求解对偶问题的时候依旧成立。
$$\{\begin{array}{l}\frac{\partial L(x,{\alpha }_i,{\lambda }_i)}{\partial x}=0\\ \frac{\partial L(x,{\alpha }_i,{\lambda }_i)}{\partial {\alpha }_i}=0\\ \frac{\partial L(x,{\alpha }_i,{\lambda }_i)}{\partial {\lambda }_i}=0\\ g_i(x)\le 0\\ h_i(x)=0\\ {\alpha }_i\ge 0\\ {\alpha }_i{h}_i(x)=0\end{array}$$
2.4.4 支持向量机模型的对偶问题
支持向量机原问题为
$$\begin{array}{rl}& ({\omega }_i,b)\to =\underset{({\omega }_i,b)}{\min }\frac{||W|{|}^2}{2}\\ & s.t.1-z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)\le 0,k=1,...,N\end{array}$$
那么拉格朗日函数为
$$L({\alpha }_i,b,{\alpha }_i,{\lambda }_i)=\frac{||W|{|}^2}{2}+\sum _k{\alpha }_k[1-z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)]$$
那么原问题等价于
$$\underset{{\omega }_k,b}{\min }\underset{{\alpha }_i;{\alpha }_i\ge 0}{\max }L({\omega }_i,b,{\alpha }_i)$$
其拉格朗日对偶问题为
$$\begin{array}{rl}& \underset{{\alpha }_i}{\max }\underset{{\omega }_i,b}{\min }L({\omega }_i,b,{\alpha }_i)\\ & s.t.{\alpha }_i\ge 0\end{array}$$
由kkt条件求解该问题。

1. 由$\nabla L=0$ 可以得到以下关系式
   $$\frac{\partial L(W,b,{\alpha }_i)}{\partial W}=W-\sum {\alpha }_k{z}^{(k)}{X}^k=0$$
   $$\frac{\partial L(W,b,{\alpha }_i)}{\partial W}=-\sum {\alpha }_k{z}^{(k)}=0$$
   代入拉格朗日函数，得到
   $$\begin{array}{rl}L({\alpha }_i,b,{\alpha }_i)& =\frac{||W|{|}^2}{2}+\sum _k{\alpha }_k[1-z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)]\\ & =\frac{1}{2}(\sum _k{\alpha }_k{z}^{(k)}{X}^{(k)})\bullet (\sum _k{\alpha }_k{z}^{(k)}{X}^{(k)})+\sum _k{\alpha }_k\{1-z^{(k)}[X^{(k)}\bullet (\sum _k{\alpha }_k{z}^{(k)}{X}^{(k)})+b)]\}\\ & =\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{z}^{(i)}{z}^{(j)}(X^{(i)}\bullet X^{(j)})-\sum _i\sum _j{\alpha }_i{z}^{(i)}{\alpha }_j{z}^{(j)}(X^{(i)}\bullet X^{(j)})-\sum _i{\alpha }_i{z}^{(i)}b+\sum _i{\alpha }_i\\ & =-\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{z}^{(i)}{z}^{(j)}(X^{(i)}\bullet X^{(j)})+\sum _i{\alpha }_i\end{array}$$
   拉格朗日对偶问题进一步简化为
   $$\begin{array}{rl}& \underset{{\alpha }_i}{\max }-\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{z}^{(i)}{z}^{(j)}(X^{(i)}\bullet X^{(j)})+\sum _i{\alpha }_i\\ & s.t.{\alpha }_i\ge 0\\ & \sum _i{\alpha }_i{z}^{(i)}=0\end{array}$$
   一般将上述求最大值问题转换为求最小值问题。
   $$\begin{array}{rl}& \underset{{\alpha }_i}{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{z}^{(i)}{z}^{(j)}(X^{(i)}\bullet X^{(j)})-\sum _i{\alpha }_i\\ & s.t.{\alpha }_i\ge 0\\ & \sum _i{\alpha }_i{z}^{(i)}=0\end{array}$$

2. 求解拉格朗日对偶问题得到参数$\{{\alpha }_i^{\ast },i=1,...,N\}$,不难得到$$W^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{z}^{(i)}{X}^{(i)}$$
   3.由函数间隔的定义，必定存在某一点使得 $1-z^{(k)}(\sum {\omega }_i{X}_i^{(k)}+b)\le 0$ 等式严格成立，即存在$X^{(\ast )}$(实际上就是离分割超平面最近的样本点)，使$$1-z^{(t)}(\sum _{i=0}^l{\omega }_i^{\ast }{X}_i^{(t)}+b^{\ast })=0$$
   $$b^{\ast }=z^{(t)}-\sum _{i=0}^l{\omega }_i^{\ast }{X}_i^{(t)}=z^{(t)}-W^{\ast }{X}^{(t)}=z^{(t)}-\sum _{i=1}^N{\alpha }_i^{\ast }{z}^{(i)}(X^{(i)}\bullet X^{(t)})$$

(对于距离分割超平面最近的样本点，那么必然存在${\alpha }_t^{\ast }>0$,其实根据KKT条件中的相容性条件也可推得上述$b^{\ast }$的关系式${\alpha }_t^{\ast }(1-z^{(t)}(\sum {\omega }_i^{\ast }{X}_i^{(t)}+b))=0$）

所以求解问题的一般步骤是：1）求解对偶问题的最优解${\alpha }_i^{\ast }$，2）按公式求解$W^{\ast }$，3）求解$b^{\ast }$。

---

参考文献：

[1]. 机器学习[M]. 周志华.
[2]. 统计学习方法[M]. 李航
[3]. Python机器学习算法[M].赵志勇.

文章导引列表：
机器学习

1. 小瓜讲机器学习——分类算法（一）logistic regression(逻辑回归)算法原理详解
2. 小瓜讲机器学习——分类算法（二）支持向量机（SVM）算法原理详解
3. 小瓜讲机器学习——分类算法（三）朴素贝叶斯法（naive Bayes）
4. 待续

---

数据分析

1. 小呆学数据分析——使用pandas中的merge函数进行数据集合并
2. 小呆学数据分析——使用pandas中的concat函数进行数据集堆叠
3. 小呆学数据分析——pandas中的层次化索引
4. 小呆学数据分析——使用pandas的pivot进行数据重塑
5. 小呆学数据分析——用duplicated/drop_duplicates方法进行重复项处理
6. 小呆学数据分析——缺失值处理（一）
7. 小呆学数据分析——异常值判定与处理（一）
8. 小瓜讲数据分析——数据清洗

---

数据可视化

1. 小瓜讲数据分析——数据可视化工程（matplotlib库使用基础篇）
2. 小瓜讲matplotlib高级篇——坐标轴设置（坐标轴居中、坐标轴箭头、刻度设置、标识设置）