ORB_SLAM2代码阅读(4)——LoopClosing线程

1.说明

在前几篇博客介绍完tracking和localmaping线程后，本文接着介绍闭环检测（LoopClosing）线程中的内容。该部分内容中有很多细节部分还没有弄清楚，暂时先将整体思路捋顺，更多细节内容以后再补充。

2.简介

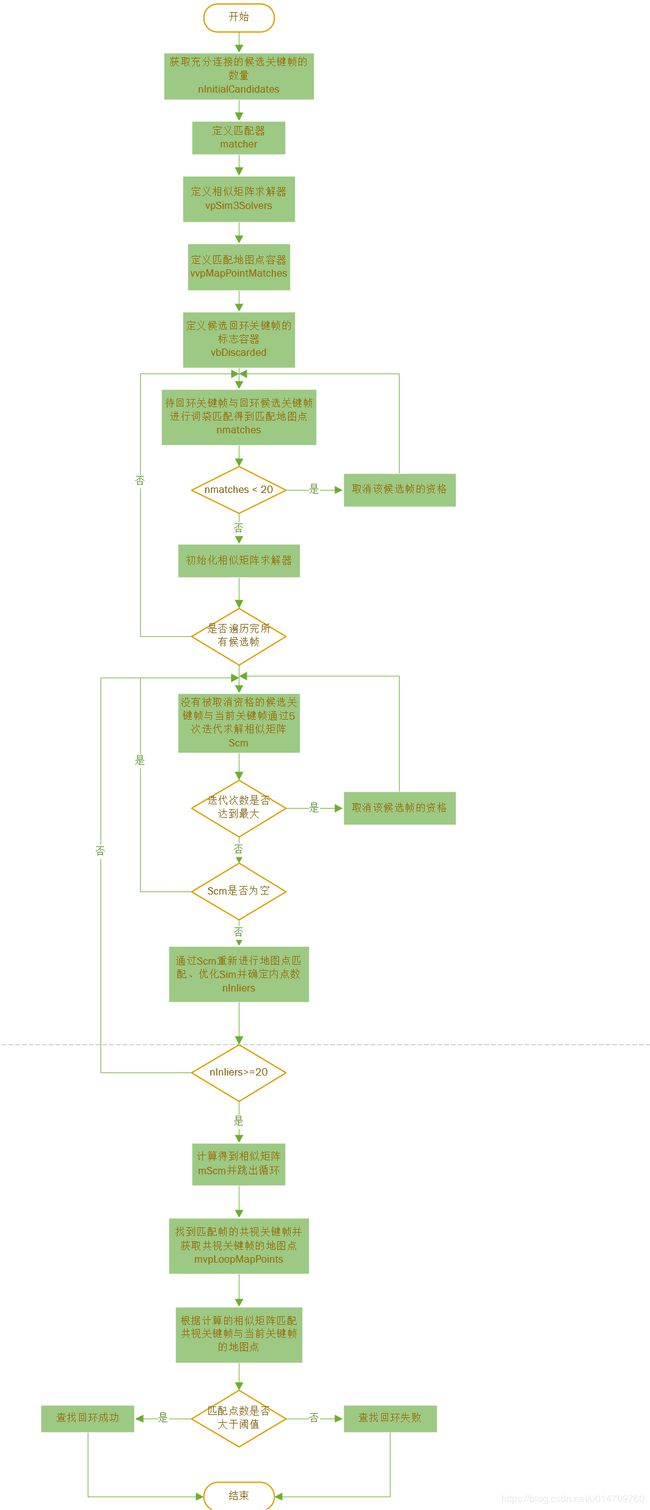
LoopClosing线程整体思路比较简介清晰，主要分为三大部分：检测回环、计算Sim3和回环校正。该线程的入口为Run()函数（相当于主函数）。

首先从流程图中看看LoopClosing线程的整体逻辑（该流程图对应Run()函数中的内容）：

其中较为重要的变量有：

变量名	变量类型	说明
mpCurrentKF	KeyFrame*	当前关键帧
mpMatchedKF	KeyFrame*	匹配关键帧
mvConsistentGroups	vector< ConsistentGroup >	所有的连续关键帧组集
mvpEnoughConsistentCandidates	vector	充分连接的候选关键帧组
mlpLoopKeyFrameQueue	list	待回环检测的关键帧队列

接下来，分别介绍检测回环、计算Sim3和回环校正三部分内容。

3.检测回环

检测回环部分对应代码中的bool LoopClosing::DetectLoop() 函数，该函数整体逻辑较为清晰，但是一致性检测部分有点不好理解，并且相关资料较少。有些内容是我自己的理解，正确性有待商榷。

检测回环的主要思想：

1. 在关键帧队列中提取队首元素作为当前关键帧。关键帧队列中的元素是局部建图线程添加的。
2. 获取当前关键帧的共视关键帧，并计算当前关键帧与每个共视关键帧之间的BOW向量得分，记录最小得分minScore。
3. 根据最小得分minScore在关键帧数据库mpKeyFrameDB中查找当前关键帧的回环候选关键帧vpCandidateKFs。
4. 对每个候选关键帧进行一致性检测。
5. 经过一致性检测后，如果存在充分连接的候选关键帧，则证明检测到了回环；否则，回环检测失败。

该过程的具体流程如下图所示：

对于计算最小得分和获取候选回环关键帧等操作并不难理解，根据最小得分查找候选回环关键帧的原理以后在进行介绍。这里主要说一下一致性检测的原理。

一致性检测部分是检测回环的关键，光看代码的话有点难理解，而且网上关于这部分介绍的也不多。接下来的内容是我自己的理解，可能不完全正确，姑且述之。

先说一下该部分涉及的变量。

变量名	变量类型	说明
vpCandidateKFs	vector	候选回环关键帧向量
pCandidateKF	KeyFrame*	当前候选关键帧
spCandidateGroup	set	候选关键帧的共视关键帧以及候选关键帧构成了"子候选组"——当前子候选组
vCurrentConsistentGroups	vector	当前连续关键帧组构成的向量
mvConsistentGroups	vector	由当前关键帧的前一关键帧确定的子连续组向量
mvpEnoughConsistentCandidates	vector	充分连接的候选关键帧组成的向量
nCurrentConsistency	int	用于记录当前子候选组的一致性

一致性检测的过程：

1. 在候选关键帧向量中选取一个候选关键帧pCandidateKF，将候选关键帧的共视关键帧和候选关键帧组成当前子候选组spCandidateGroup。
2. 遍历 mvConsistentGroups 中的子连续组。如果 mvConsistentGroups 中的子连续组sPreviousGroup包含当前子候选组中的关键帧，则说明该子连续组sPreviousGroup与当前子候选组是相连的。
3. 如果当前子候选组与之前的子连续组是相连的，则将当前子候选组添加到vCurrentConsistentGroups中，并将nCurrentConsistency设置为与之相连的子连续组的一致性加一，即nCurrentConsistency = nPreviousConsistency + 1;然后将当前子候选组添加到vCurrentConsistentGroups中。
4. 如果nCurrentConsistency大于阈值，则说明当前子候选组有足够多的连接组。因此将当前候选关键帧pCandidateKF添加到mvpEnoughConsistentCandidates中用于下一步的Sim3计算。
5. 如果当前子候选组与之前的连续组均无交集，则将其一致性置为0，然后将其添加到vCurrentConsistentGroups中。
6. 重复该过程直至遍历完所有的候选关键帧。
7. 用vCurrentConsistentGroups更新mvConsistentGroups。

一致性检测的原理：
首先要明白回环处的关键帧会有一定时间和空间上的连续性。在进行一致性检测的时候，mvConsistentGroups中保存着由上一关键帧确定的连续关键帧组，这些连续关键帧组相当于确定了一个回环处的大致范围。由当前关键帧确定的候选关键帧构建的子候选组与mvConsistentGroups中的连续关键帧组由交集，则说明该候选关键帧在回环处附近。一旦由候选关键帧构建的子候选组与mvConsistentGroups中的多个连续关键帧组有交集时，则说明该候选关键帧在回环处的可能性更大，因此将其加入到mvpEnoughConsistentCandidates中用于下一步计算相似矩阵。

举例说明：

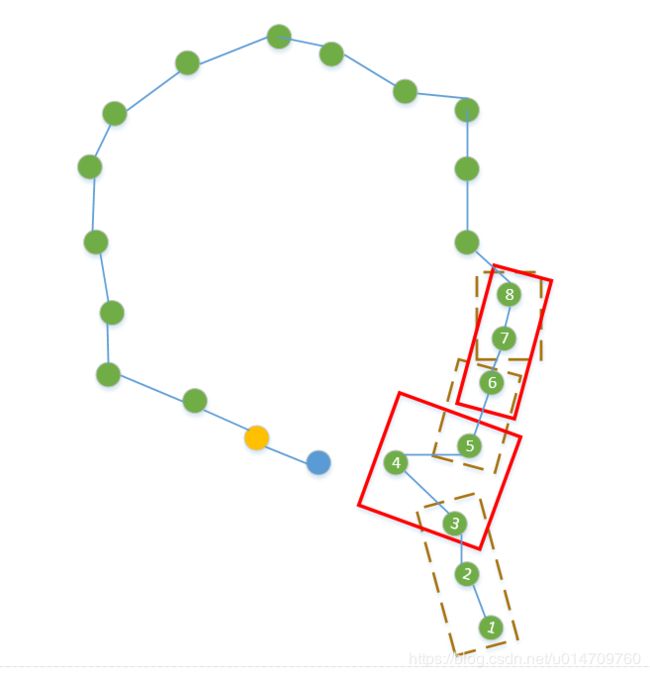
图中的蓝色点为当前关键帧，黄色点为当前关键帧的上一关键帧；棕色框框住的内容为mvConsistentGroups中的连续关键帧组（P1：123，P2:56，P3: 78）。假设P1的一致性指数为2，P2和P3的一致性指数为1；当前关键帧确定的候选关键帧为节点4和节点7，节点4构成的子候选组为Q1：345，节点7构成的子候选组为Q2：678。子候选组Q1与P1和P2均相连，所以一致性指数为3，满足条件。因此候选关键帧7将被添加到mvpEnoughConsistentCandidates中用来进行下一步计算。子候选组Q2与P2和P3相连，但是其一致性指数为2，不满足条件。因此要被剔除。

该部分内容对应的代码为：

    mvpEnoughConsistentCandidates.clear();     
    // 当前的连续组
    vector vCurrentConsistentGroups;
    vector vbConsistentGroup(mvConsistentGroups.size(),false);
    for(size_t i=0, iend=vpCandidateKFs.size(); i spCandidateGroup = pCandidateKF->GetConnectedKeyFrames();
        spCandidateGroup.insert(pCandidateKF);
        
        bool bEnoughConsistent = false;
        bool bConsistentForSomeGroup = false;
	    
        //遍历之前的"子连续组"
        for(size_t iG=0, iendG=mvConsistentGroups.size(); iG sPreviousGroup = mvConsistentGroups[iG].first;
            bool bConsistent = false;
            for(set::iterator sit=spCandidateGroup.begin(), send=spCandidateGroup.end(); sit!=send;sit++)
            {
                if(sPreviousGroup.count(*sit))   //如果之前子连续组中包含"子候选组"中的帧,则说明该关键帧组与之前的组是连续的
                {
                    bConsistent=true;
                    bConsistentForSomeGroup=true;
                    break;
                }
            }

            if(bConsistent)  // 如果与之前的连续组是连续的  则将它加入到当前连续组中
            {
                int nPreviousConsistency = mvConsistentGroups[iG].second;
                int nCurrentConsistency = nPreviousConsistency + 1;
                if(!vbConsistentGroup[iG])   // 如果当前连续组没有在当前连续组集中,则将其加入
                {
                    ConsistentGroup cg = make_pair(spCandidateGroup,nCurrentConsistency);
                    vCurrentConsistentGroups.push_back(cg);    //当前连续组
                    vbConsistentGroup[iG]=true; //this avoid to include the same group more than once 
                }
                if(nCurrentConsistency>=mnCovisibilityConsistencyTh && !bEnoughConsistent)  
                {
                    mvpEnoughConsistentCandidates.push_back(pCandidateKF);
                    bEnoughConsistent=true; //this avoid to insert the same candidate more than once
                }
            }
        }
        // If the group is not consistent with any previous group insert with consistency counter set to zero
        if(!bConsistentForSomeGroup)
        {
            ConsistentGroup cg = make_pair(spCandidateGroup,0);
            vCurrentConsistentGroups.push_back(cg);
        }
    }
    // Update Covisibility Consistent Groups   更新连续组
    mvConsistentGroups = vCurrentConsistentGroups;

4.计算Sim3

一旦检测到闭环，接下来就要根据选取的候选关键帧来计算相似变换矩阵并重新计算相关的地图点。可以说计算相似矩阵是LoopClosing线程的关键所在。

在介绍该线程中如何计算相似矩阵之前，先了解一下相似变换。
我们知道刚体运动可以分解为旋转运动和平移运动，分别用旋转矩阵R和平移向量t表示。为了能使刚体运动能够进行线性计算，我们构造了变换矩阵T（变换矩阵T也成为等距变换）：
$$T=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]$$
相似变换相当于在等距变换的基础上加上一个尺度因子，表示为
$$S=\left[\begin{array}{cc}sR& t\\ 0& 1\end{array}\right]$$
为了直观的体验一下等距变换与相似变换的区别，我们可以看一下相似变换对二维图像的处理效果。

可以直观的看出图像经过相似变换之后，与等距变换相比，相似变换的结果尺度发生了很大的变化。这个效果类似于对图像下采样，构建图像金字塔的效果。

4.1 为什么在进行回环检测的时候需要计算相似变换矩阵，而不是等距变换？

回答这个问题需要从单目slam的尺度不确定性说起。在单目视觉里程计中，求解相机之间的位姿需要运用对极约束求解本质矩阵，但是本质矩阵具有尺度等价性，这就造成了单目slam的尺度不确定性。为了能使单目slam系统能够正常运行，在起始时刻，有一个初始化过程。初始化的过程是指在单目视觉中，对两张图像的平移向量 t 归一化，相当于固定了尺度。虽然我们不知道它的实际长度为多少，但我们以这时的 t 为单位 1，计算相机运动和特征点的 3D 位置。 在初始化之后，就可以用 3D-2D 来计算相机运动。

在初始化过程完成之后，相当于两张图像之间的平移关系已经确定，这时可以利用三角化的方式计算特征点的空间坐标，在得到特征点的空间坐标之后便可以通过3D-2D的方式求解图像之间的运动关系，从而完成视觉里程计的计算过程。换句话说，这个过程就是利用图像间的运动关系计算特征点的空间坐标，然后利用特征点的空间坐标和像素坐标计算图像间的运动关系的不断向前重复进行的过程。理想情况下，如果系统没有任何误差，那么在整个过程中尺度不会发生漂移。但是由于累积误差的存在，使得尺度会发生漂移。

系统为了能够修正整个尺度漂移，所以在回环检测阶段计算相似变换矩阵。通过计算得到的尺度因子修正累计误差造成的尺度漂移。而变换矩阵中并不在尺度因子，所以在回环检测的时候需要计算相似变换矩阵而不是等距变换。

4.2 累积误差是如何使尺度因子发生漂移的？

先弄清尺度因子到底表示的是什么物理意义。在初始化的过程中，将平移向量t 进行了归一化，也就是说令平移向量的模值为1，但它的真实模值并不是1。所以平移向量的真实模值与归一化之后的模值之比就是尺度因子。

在将平移向量进行归一化处理后，我们会运用三角化的方式计算特征点的空间坐标（也就是计算特征点的深度），所以尺度因子也可以表示为特征点的真实深度与用归一化平移向量计算出的深度之比。如果系统没有任何误差，那么在整个过程中尺度不会发生漂移。但是由于存在误差，并且误差会进行累计，所以系统运行时间越长，我们计算出的特征点的深度与特征点的真实深度之比（即尺度因子）就会发生变化。也就是发生了尺度漂移。

而且尺度漂移和累积误差是相互影响的，尺度漂移越严重，累积误差越大；累积误差越大，也会导致尺度漂移越严重。

使用双目相机或深度相机的时候为什么要计算相似矩阵？
理论上来说，用双目相机或深度相机不存在尺度不确定的问题。从而也就不用考虑尺度漂移的问题。但是相似矩阵在变换矩阵的基础上多了尺度因子，如果能确定相似矩阵那肯定也就能确定变换矩阵。
这种理解方式是我个人的理解方式，我也不知道正确与否。

4.3 计算Sim3的过程

在代码中，计算Sim3的主要思路是：

1. 待回环关键帧（当前关键帧）与回环候选关键帧进行词袋匹配，得到匹配地图点
2. 如果匹配地图点的数量满足要求，则根据地图点来初始化相似矩阵求解器。在该过程中会剔除一部分不满足要求的候选关键帧
3. 迭代的方式求解相似矩阵。如果迭代次数达到最大，则剔除该候选关键帧。
4. 根据计算得到的相似矩阵重新进行地图点匹配，然后用重新匹配得到的地图点优化相似矩阵。根据优化后的内点数来判断相似矩阵是否满足要求。到此，相机矩阵的计算已经结束。
5. 找到匹配帧的共视关键帧并获取共视关键帧的地图点mvpLoopMapPoints。
6. 将mvpLoopMapPoints投影匹配的方式与当前关键帧进行匹配。得到的匹配地图点数量满足要求，则说明成功找到了回环，否则失败。

总结一下，该部分的内容就是：匹配地图点，迭代计算Sim3，重新匹配地图点，优化Sim3，再次匹配地图点判断回环是否真的发生。

至于Sim3的计算原理，后面单独写一篇博客来记录。

该部分内容具体的流程可以用以下流程图表示：

5.回环校正

在经过回环检测和相似矩阵计算之后，接下俩就要进行回环校正。在进行回环校正之前，当前关键帧、匹配关键帧和相似矩阵等变量均已知。

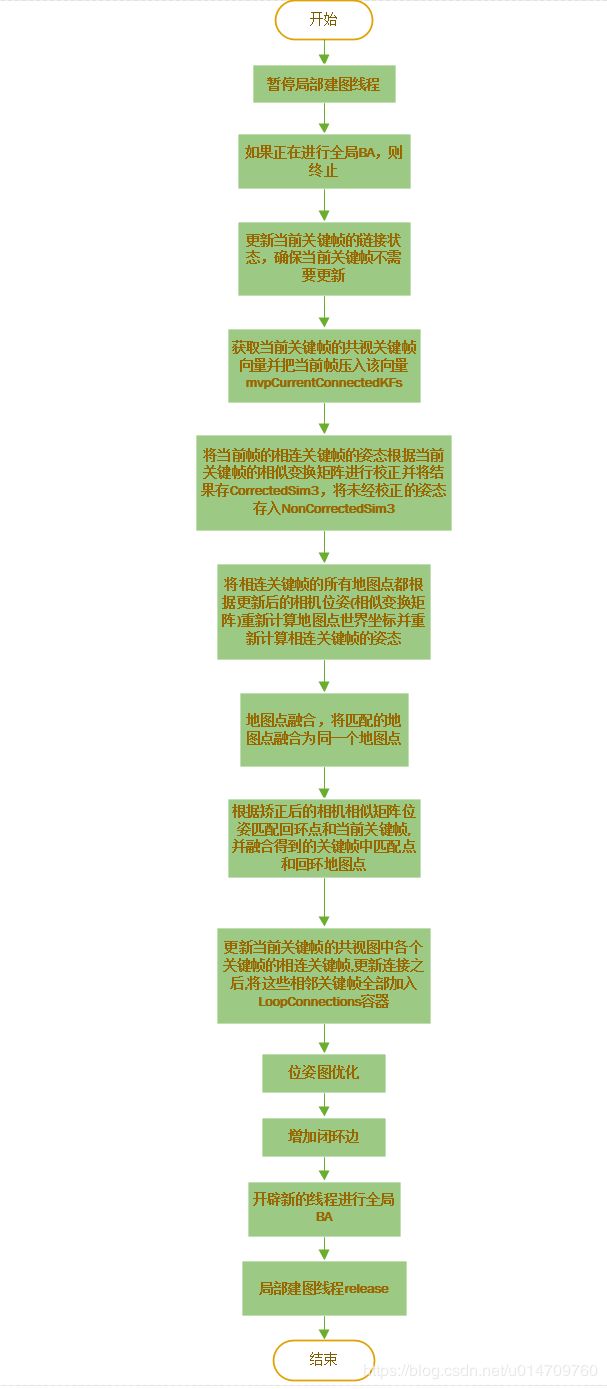
回环校正的主要步骤为：

1. 准备工作：暂停局部建图线程，停止正在进行的全局优化，更新当前关键帧的连接情况。
2. 构建当前关键帧的连续组，并根据计算出的相似变换矩阵校正连续组中关键帧的位姿。
3. 将相邻关键帧的所有地图点都根据更新后的相机位姿(相似变换矩阵)重新计算地图点世界坐标 。
4. 进行地图点融合 。将当前帧的地图点和ComputeSim3过程中当前关键帧与候选帧的共视关键帧匹配得到的地图点进行融合。
5. 根据矫正后的相机相似矩阵位姿匹配回环点和当前关键帧,并融合得到的关键帧中匹配点和回环地图点。代码中的SearchAndFuse()函数。
6. 更新当前关键帧的共视图中各个关键帧的相连关键帧,更新连接之后,将这些相邻关键帧全部加入LoopConnections容器。
7. 进行位姿图优化和全局BA。

对于该过程中的SearchAndFuse()部分、位姿图优化和全局BA部分，还没有仔细研究。以后有时间研究之后再来补充。

具体流程可以参考以下流程图：