视觉SLAM常见的QR分解SVD分解等矩阵分解方式求解满秩和亏秩最小二乘问题(最全的方法分析总结)
关于这个问题的内容比较多,也整理了相当一段时间,在写内容之前,我需要引用一些牛人的名人名言,以壮士气。
(1)故不积跬步,无以至千里;不积小流,无以成江海-荀子
(2)只收藏,不点赞的同学,人心都是肉长的。。。地主家也没有余粮啊。。。我想说的是。。。不赞不是好码农-马克.wangshuai
(纯粹copy)
内容一
首先直接给出AX=B解的情况:
(1)R(A)< r(A|B),方程组无解
(2)r(A)=r(A|B)=n,方程组有唯一解
(3)r(A)=r(A|B) < n,方程组有无穷解
(4)r(A)>r(A|B),这种情况不存在
其中r()代表矩阵的秩,A|B是增广矩阵,n是X未知数个数。通过下面的例子理解下这个结论,假设x=[x1,x2],其实就便沉了一个二元一次方程组求解问题。
(1)A[1,1;0,0],B=[1,1],AX=B方程组变成了下式,这自然没有解,因为方程组的第二个式子是的0=1,与事实不符。
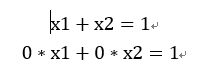
(2)A[1,1;0,1],B=[1,1],AX=B方程组变成了下式,这自然有唯一解,解为X=[0,1].

(3)A[1,1;0,0],B=[1,0],AX=B方程组变成了下式,这自然有无穷解,因为第二项消掉了,方程只剩下第一项,一个方程式,两个未知量。

这里就引出最小二乘问题,最小二乘问题就是用来解决第二、三种情况求最优解。当出现第二种情况下(也就是A满秩下,称为满秩最小二乘问题),为了提高效率通常使用QR分解、LTLD分解、Cholesky分解和SVD分解(奇异分解)等。当出现第三种情况时(也就是A秩亏,称为亏秩最小二乘问题),只能使用SVD分解方法,其他方法将失效。下面分别介绍QR分解、LTLD分解、cholesky分解和SVD分解的方法,然后探讨其对最小二乘的解法。
内容二:
这里有必要提下线性最小二乘问题

可见一般在视觉SLAM中后端优化就是约束项大于未知数的个数(超定问题),采用最小二乘问题求解
内容三:
为什么需要矩阵分解
个人认为,首先,当数据量很大时,将一个矩阵分解为若干个矩阵的乘积可以大大降低存储空间;其次,可以减少真正进行问题处理时的计算量,毕竟算法扫描的元素越少完成任务的速度越快,这个时候矩阵的分解是对数据的一个预处理;再次,矩阵分解可以高效和有效的解决某些问题;最后,矩阵分解可以提高算法数值稳定性,关于这一点可以有进一步的说明。
例如方程:

结果变成了上式,可以看出当方程组中的常数矩阵发生微小的扰动时,会导致最终的结果发生较大的变化,这种结果的不稳定不是因为方程求解的方法,而是方程组矩阵本身的问题。这回给我们带来很大的危害,例如像上面的情况,计算机求解出现舍入误差,矩阵本身不好的话会直接导致结果失败。
当对矩阵A或者b进行小扰动的时候,最后影响结果的是||A||||A^(-1) ||,与矩阵病态性成正相关。定义矩阵的条件数cond(A)= ||A||||A^(-1) ||来描述矩阵的病态程度,一般认为小于100的为良态,条件数在100到1000之间为中等程度的病态,条件数超过1000存在严重病态。以上面的矩阵A为例,采用2范数的条件数cond(A)=222.9955, 矩阵处于中等病态程度。
矩阵其实就是一个给定的线性变换,特征向量描述了这个线性变换的主要方向,而特征值描述了一个特征向量的长度在该线性变换下缩放的比例,对开篇的例子进一步观察发现,A是个对称正定矩阵,A的特征值分别为λ1:14.93303437 和λ2:0.06696563,两个特征值在数量级上相差很大,这意味着b发生扰动时,向量x在这两个特征向量方向上的移动距离是相差很大的——对于λ1对应的特征向量只需要微小的移动就可到达b的新值,而对于λ2,由于它比起λ1太小了,因此需要x做大幅度移动才能到达b的新值,于是悲剧就发生了.
内容四:
视觉SLAM中常用矩阵
1.正交矩阵
有一种经典的矩阵,叫正交矩阵, 什么叫正交矩阵呢?其实某种意义上,正交矩阵也是通过矩阵乘法来定义的。 如果一个矩阵和它的转置矩阵的乘积为单位矩阵, 那么这个矩阵就是正交矩阵。李群中旋转矩阵就是一种正交阵,所以一般其逆的形式直接写成转置,因为转置计算简单。
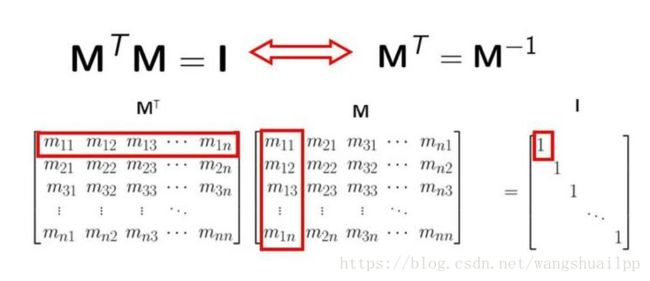
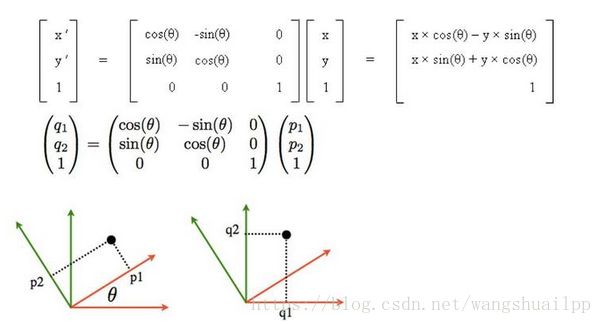
为什么叫正交矩阵呢?因为如果我们把这个矩阵写成向量的形式, 那么这些向量除了自己和自己的点积为1,其他任意两个不同向量之间的点积全部为0.而向量点积为0的情况叫正交。正交矩阵是因此得名的,其实就可以理解成一组基,也就是坐标系。为什么要讲正交矩阵呢?还记得在矩阵的加法分解里面,有求逆矩阵的情况么?试想一下,如果不要求逆矩阵了,而是求解转置矩阵的话,那是不是异常方便?对的,这就是正交矩阵的强大的优势,因此下面的矩阵分解中都希望直接转换成正交矩阵相乘的形式。

我们可以看到正交矩阵,并不改变物体的形状,但是进行了旋转。

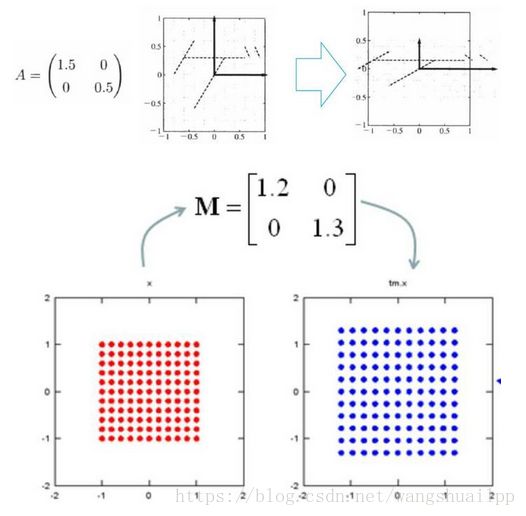
2.对角矩阵
乘以一个对角矩阵,好比对每个坐标轴进行缩放,包括方向,和压缩。正数的乘法:正数好比在原方向上的缩放, 大于1,表示伸长,小于1,表示缩小。负数的乘法:负数表示反反向。零的乘法:零表示空间压缩。

3. 三角矩阵
和对角矩阵相比,三角矩阵要多一些角上的元素,那么这些元素有什么作用呢?上三角矩阵:上三角矩阵的作用好比进行右上的切变,水平的斜拉。下三角矩阵:同样是切边,不过是往左下切边,垂直方向的下拉。
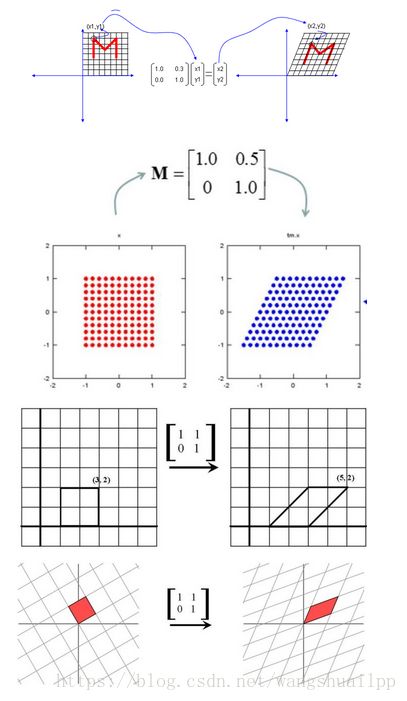

矩阵分解就是分解成上面三种形式,综上所述,矩阵分解的几何意义就是把一个线性变换分解开来,分别是缩放,切边和旋转。矩阵因子的作用就是要把缩放,切边和旋转分解出来理解一个矩阵的作用。
内容五:
1.QR分解
当A是非奇异的实方阵(满秩,只有方阵才存在奇异性,奇异矩阵秩亏,行列式为0,非奇异矩阵满秩,行列式不为0),实方阵A能够表示成一个正交矩阵Q(QTQ=I)与上三角矩阵R的积,QR分解的实际计算有很多方法,例如 Givens 旋转、Householder 变换,以及 Gram-Schmidt正交化等等。A=Q*R称为A的QR分解。如下图所示

前面我们提到单位矩阵也是正交矩阵, 所以正交矩阵可以看成是坐标系的转换。所以有时候,QR分解也可以表示成如下形式。
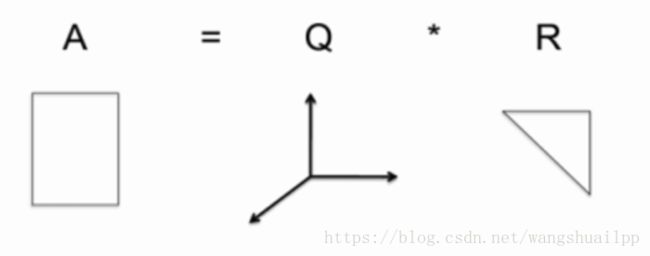
QR分解的意义
从几何上QR分解,就是先进行旋转,然后再进行切变的过程。

2.LDLT分解
对称矩阵A可以分解成一个下三角矩阵L(Lower下)和一个对角矩阵D(Diagonal对角线)以及一个下三角矩阵L的转置LT三个矩阵相乘的形式。如下式

由A的分解可知AT=A,即A的转置等于A矩阵本身。
LDLT分解解满秩最小二乘问题
一般无法得到满足对称矩阵A,因此需要使对ATA(满足对称)进行分解。将求解问题转换成下面的式子

由于r(A)=n,所以ATA是对称(正定)矩阵,式子有唯一解,使用LDLT分解的步骤是:
(1)定义矩阵C=AT*A,d=AT*b;
(2)对C进行cholesky分解C=L*D*LT,原式变成L*D*LT*x=d
(3)令y=LT*x,原式变成L*D*y=d,求解此方程得到y,然后求解y=LT*x得到x。
LDLT分解速度要快于QR分解。
3.Cholesky分解
Cholesky分解是LDLT分解的一种特殊形式,也就是其中的D是单位矩阵。正定对称矩阵 A可以分解成一个下三角矩阵L和这个下三角矩阵L的转置LT相乘的形式。如下式

Cholesky分解解满秩最小二乘问题
一般无法得到满足对称矩阵A,因此需要使对ATA(满足对称)进行分解。将求解问题转换成下面的式子
![]()
由于r(A)=n,所以ATA是对称正定矩阵,式子有唯一解,使用cholesky分解的步骤是:
(1)定义矩阵C=AT*A,d=AT*b;
(2)对C进行cholesky分解C=G*GT,原式变成G*GT*x=d
(3)令y=GT*x,原式变成G*y=d,求解此方程得到y,然后求解y=GT*x得到x。
Cholesky分解要快于LDLT分解。
4.SVD分解
矩阵的奇异值分解(SVD)在最优化问题、特征值问题、最小二乘问题及广义逆问题中有巨大作用,奇异值分解将QR分解推广到任意的实矩阵,不要求矩阵式可逆,也不要求是方阵。奇异值和特征值相似的重要意义,都是为了提取出矩阵的主要特征。假设A是一个m∗n阶矩阵,如此则存在一个分解m阶正交矩阵U、非负对角阵Σ和n阶正交矩阵V使得
A=UΣVT

Σ对角线上的元素Σi,i即为A的奇异值。而且一般来说,我们会将Σ上的值按从大到小的顺序排列。
通过上面对SVD的简单描述,不难发现,SVD解决了特征值分解中只能针对方阵而没法对更一般矩阵进行分解的问题。所以在实际中,SVD的应用场景比特征值分解更为通用与广泛。将将上面的SVD分解用一个图形象表示如下。

截止到这里为止,很多同学会有疑问了:你这不吃饱了撑得。好好的一个矩阵A,你这为毛要将他表示成三个矩阵。这三个矩阵的规模,一点也不比原来矩阵的规模小好么。而且还要做两次矩阵的乘法。要知道,矩阵乘法可是个复杂度为O(n3)的运算。如果按照之前那种方式分解,肯定是没有任何好处的。矩阵规模大了,还要做乘法运算。关键是奇异值有个牛逼的性质:在大部分情况下,当我们把矩阵Σ里的奇异值按从大到小的顺序呢排列以后,很容易就会发现,奇异值σ减小的速度特别快。在很多时候,前10%甚至前1%的奇异值的和就占了全部奇异值和的99%以上。换句话说,大部分奇异值都很小,基本没什么卵用。。。既然这样,那我们就可以用前面r个奇异值来对这个矩阵做近似。于是,SVD也可以这么写:
Am×n≈Um×rΣr×rVr×n
其中,r≪m,r≪n。如果用另外一幅图描述这个过程,如下图:

看了上面这幅图,同学们是不是就恍然大悟:原来的那个大矩阵A,原来可以用右边的那三个小矩阵来表示。当然如果r越大,跟原来的矩阵相似度就越高。如果r=n,那得到的就是原来的矩阵A。但是这样存储与计算的成本就越高。所以,实际在使用SVD的时候,需要我们根据不同的业务场景与需求还有资源情况,合理选择r的大小。本质而言,就是在计算精度与空间时间成本之间做个折中。
SVD分解意义
按照前面给出的几何含义,SVD 分解可以看成先旋转,然后进行分别缩放,然后再旋转的过程。

SVD分解解满秩(亏秩)最小二乘问题
SVD分解不仅可以解决满秩最小二乘问题,最重要的是可以解决亏秩最小二乘问题(r(A)< n,理解下其实就相当于这里取r < n的情况),而前面的方法在秩亏的时候都会失效。
设A的SVD分解为:

