学习率优化（一）
上节介绍了反向传播时权值更新方法，更新隐含层：
；更新输出层：
。看似已经完美的解决了问题，但是
怎么取值呢？
我们把问题转化到求二次函数极值问题，例如
，如果用梯度下降法求函数极值，每一次
的取值为
，一步步趋近极小值。
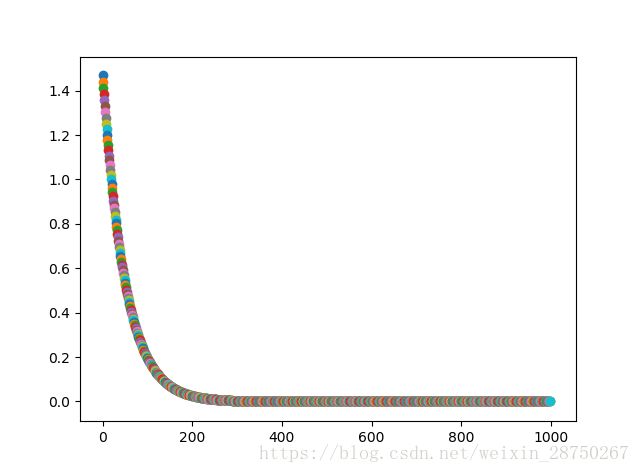
如果采用固定学习率：，初始值取
，学习率使用0.01：
分析：经过200次迭代，
；经过1000次迭代，
；
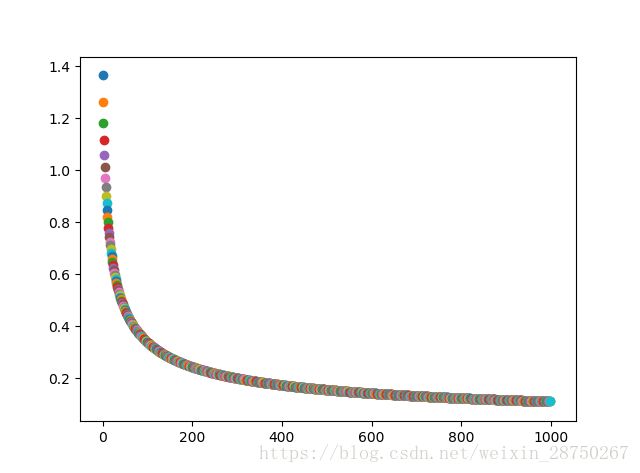
效果还可以，但这个学习率只使用于，如果改变函数还可以这个效果吗？还采用学习率0.01，
，初始值取：
分析：经过200次迭代，
；经过1000次迭代，
；效果不好，学习率不再适用。附上固定学习率的python代码：
import matplotlib.pyplot as plt
def g(x):
return 4.0*x**3
def f(x):
return x**4
if __name__ == '__main__':
x =1.5
a = 0.01
# 固定学习率
for i in range(1000):
d = g(x)
x -= d * a
if i == 200:
print(x)
plt.scatter(i,x)
print(x)
plt.show()
回溯线性搜索：
基于Armijo准则计算搜素方向上的最大步长，其基本思想是沿着搜索方向移动一个较大的步长估计值，然后以迭代形式不断缩减步长，直到该步长使得函数值
相对与当前函数值
的减小程度大于预设的期望值(即满足Armijo准则)为止。
意思就是说，按学习率缩小一次后得到新值
，如果
设定为我们的期望值，如果经过学习后可以达到，那么这个学习率就是符合要求的学习率；
。
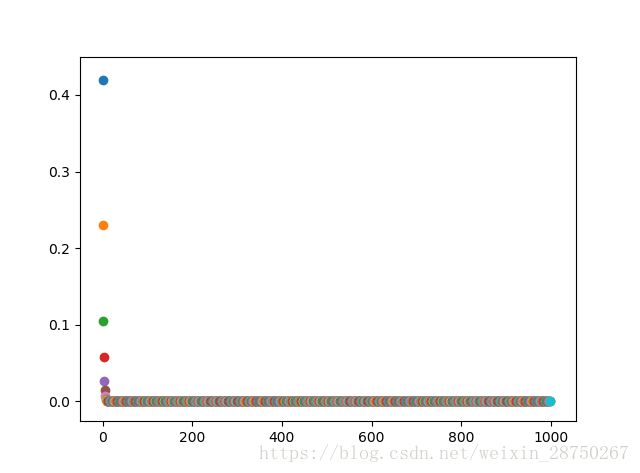
分析：经过12次迭代后，
，经过1000次迭代后
，效果不错。
import matplotlib.pyplot as plt
def g(x):
return 4.0*x**3
def f(x):
return x**4
def armijo(x,d,a):
c1 = 0.3
now = f(x)
next = f(x - a*d)
count =30
while next < now:
a *= 2
next = f(x - a*d)
count-=1
if count == 0:
break
count = 50
while next > now-c1*a*d*d:
a /=2
next = f(x - a*d)
count -=1
if count == 0:
break
return a
if __name__ == '__main__':
x =1.5
a = 0.01
#回溯线性搜索
for i in range(1000):
d = g(x)
a1 = armijo(x,d,a)
x -= d * a1
if i == 12:
print(x,a1)
plt.scatter(i,x)
print(x,a1)
plt.show()
二次插值法：
如上述代码，第一个循环，如果沿负梯度方向下降微小的值，
会恒成立，但我们每一次都增大学习率，当某一次步子迈的太大，就会不满足，Armijo准则则是再减小学习率，那么二次插值法则是构造一个二次近似函数：
；那么导数为0的最优值为：![\alpha_{1} =\frac{h^{'}(0)\alpha _{0}^{2} }{2[h^{'}(0)\alpha_{0}+h(0)-h(\alpha _{0})]}](http://img.e-com-net.com/image/info8/49994bcf6e004727aaed21d63135c03f.gif){kind=small}
，若
满足Armijo准则，则输出该学习率，否则继续迭代。
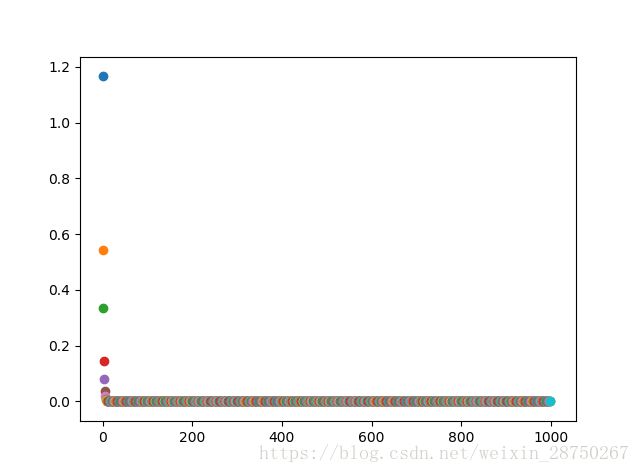
分析，经过12次迭代
，，经过1000次迭代，
，效果和回溯法差不多，么有提升。
import matplotlib.pyplot as plt
def g(x):
return 4.0*x**3
def f(x):
return x**4
def getA_quad(x,d,a):
c1 = 0.3
now = f(x)
next = f(x - a*d)
count =30
while next < now:
a *= 2
next = f(x - a*d)
count-=1
if count == 0:
break
count = 50
while next > now-c1*a*d*d:
b=d*a*a/(now+d*a-next)
b /=2
if b<0:
a /=2
else:
a = b
next = f(x - a*d)
count -=1
if count == 0:
break
return a
if __name__ == '__main__':
x =1.5
a = 0.01
#插值法
for i in range(1000):
d = g(x)
a1 = getA_quad(x, d, a)
x -= d * a1
if i == 12:
print(x)
plt.scatter(i, x)
print(x)
plt.show()
总结：
[一阶方法] 随机梯度
SGD(Stochastic Gradient Descent)是相对于BGD(Batch Gradient Descent)而生的。BGD要求每次正反向传播，计算所有Examples的Error，这在大数据情况下是不现实的。最初的使用的SGD，每次正反向传播，只计算一个Example，串行太明显，硬件利用率不高。后续SGD衍生出Mini-Batch Gradient Descent，每次大概推进100个Example，介于BGD和SGD之间。现在，SGD通常是指Mini-Batch方法，而不是早期单Example的方法。
一次梯度更新，可视为：
；
为参数，
为时序，
为更新量，为学习率，
为梯度。
以上介绍的回溯法和插值法都属于基于一阶随机梯度的方法，还有基于二阶随机梯度的方法；后续章节再介绍几种常规优化方法。
[二阶方法] 牛顿法
二阶牛顿法替换梯度更新量：
；
为参数的二阶导矩阵，称为Hessian矩阵。
牛顿法，用Hessian矩阵替代人工设置的学习率，在梯度下降的时候，可以完美的找出下降方向，不会陷入局部最小值当中，是理想的方法。但是，求逆矩阵的时间复杂度近似
，计算代价太高，不适合大数据。