2019独角兽企业重金招聘Python工程师标准>>> ![]()
十二步解N-S方程之第四步
通过前面的学习,我们已经知道如何去解线性和非线性的一维对流方程,而且也知道CFL是如何影响数值求解的。在这里我们考虑一维扩散方程,如下所示:
import numpy as np
import matplotlib.pyplot as plt
#
nx=41
dx=2.0/(nx-1)
nt=20
nu=0.3
sigma=0.2
dt=sigma*dx**2/nu
#
u=np.ones(nx)
u[0.5/dx:1+1/dx]=2.0
#
u0=np.ones(nx)
u0=u.copy()
#
un=np.ones(nx)
#
for n in range(nt):
un=u.copy()
for i in range(1,nx-1):
u[i]=un[i]+nu*dt/dx**2*(un[i+1]-2*un[i]+un[i-1])
plt.figure()
xc=np.linspace(0,2,nx)
plt.plot(xc,u,linewidth=2.0,label="converged")
plt.plot(xc,u0,linewidth=2.0,label="initial")
plt.legend(loc='upper right')
plt.savefig("F:\PYTHON\python_cfd\step4.png",dpi=150)
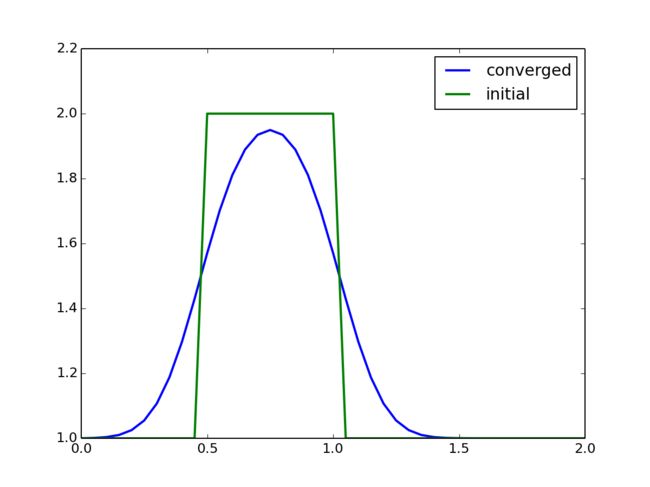
plt.show()运行结果如下图所示: