【算法】超图的理解

在现实生活中，我们把两个节点的连线称为边，由边与节点组成的图形叫做图，如下图。

其实上面这张图也叫做2阶超图，因为每一条边上只有2个节点。

更一般的，当一条边上的节点数变为任意个时，我们把这条边叫做超边

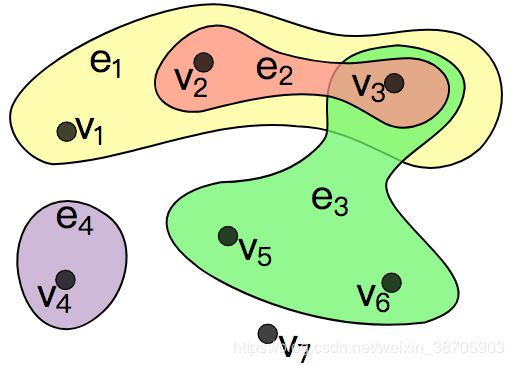
例如下图中，四个颜色分别代表了四条超边：

• 黄色边e1上有3个节点（v1,v2,v3）；
• 红色边e2上有两个节点（v2,v3）；
• 绿色边e3上有三个节点（v3,v5,v6）；
• 紫色边e4上有一个节点（v4）。

由这四条超边组成的图，叫做超图

定义：
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. Formally, a hypergraph $H$ is a pair $H=（X,E）$ where $X$ is a set of elements called nodes or vertices, and $E$ is a set of non-empty subsets of $X$ called hyperedges or edges.
在上图中，$X=\{v1,v2,v3,v4,v5,v5,v6,v7\}$，$E=\{e1,e2,e3,e4\}=\{\{v1,v2,v3\},\{v2,v3\},\{v3,v4,v5\},\{v4\}\}$

每个边所包含的顶点个数都是相同且为k个的，就可以被称为k阶超图。三阶超图如下所示：

参考：https://blog.csdn.net/TerreHX/article/details/79433848