视觉SLAM十四讲学习笔记——第七章 视觉里程计
视觉SLAM十四讲学习笔记——第七章 视觉里程计
- 7.1 特征点法
- 7.1.1 特征点
- 7.1.2 ORB 特征
- 7.1.3
- 7.2 实践:特征提取和匹配
- 7.3 2D-2D: 对极几何
- 7.3.1 对极约束
- 7.3.2 本质矩阵
- 7.3.3 单应矩阵
- 7.4 实践:对极约束求解相机运动
- 7.4.1 讨论
- 7.5 三角测量
- 7.6 实践:三角测量
- 7.7 3D-2D: PnP
- 7.7.1 直接线性变换
- 7.7.2 P3P
- 7.7.3 Bundle Adjustment

7.1 特征点法
VO 的实现方法,按是否需要提取特征,分为特征点法的前端以及不提特征的直
接法前端,基于特征点法的前端,长久以来(直到现在)被认为是视觉里程计的主流方法。
7.1.1 特征点
- 从图像中选取比较有代表性的点,这些点在相机视角发生少量变化后会保持不变,所以会在各个图像中找到相同的点,这些点称为特征点,也称为图像特征。
- 特征点是图像里一些特别的地方,可以把图像中的角点、边缘和区块都当成图像中有代表性的地方。角点是最具有特征的属性。
- 朴素的角点不易满足要求,而人工设计的特征点具有很好的性质:
- 可重复性:相同的“区域”可以在不同的图像中被找到
- 可区别性:不同的“区域”有不同的表达
- 高效率:同一图像中,特征点的数量应远小于像素的数量
- 本地性:特征仅与一小片图像区域相关。
- 特征点由关键点和描述子两部分组成
- 关键点是指该特征点在图像里的位置,有些特征点还具有朝向、大小等信息。
- 描述子通常是一个向量,按照某种人为设计的方式,描述了该关键点周围像素的信息,描述子是按照“外观相似的特征应该有相似的描述子”的原则来设计
- 只要两个特征点的描述子在向量空间上的距离相近,就可以认为它们是同样的特征点
- SIFT质量高但速度慢,成本高;FAST速度快但质量低,ORB是两者很好的折中
7.1.2 ORB 特征
- ORB 特征亦由关键点和描述子两部分组成。关键点称为“Oriented FAST”,是
一种改进的 FAST 角点,描述子称为 BRIEF。 - 提取 ORB 特征分为两个步骤:
- FAST 角点提取:找出图像中的” 角点”。ORB 中计算了特征点的主方向,为后续的 BRIEF 描述子增加了旋转不变特性
- BRIEF 描述子:对前一步提取出特征点的周围图像区域进行描述。
- FAST 是一种角点,主要检测局部像素灰度变化明显的地方,速度快,它的思
想是:如果一个像素与它邻域的像素差别较大(过亮或过暗) , 那它更可能是角点。 - FAST的检测过程:
- 在图像中选取像素 p p p ,假设它的亮度为 I p I_p Ip 。
- 设置一个阈值 T T T (比如 I p I_p Ip 的 20 % 20\% 20%) 。
- 以像素 p p p 为中心, 选取半径为 3 的圆上的 16 个像素点。
- 假如选取的圆上,有连续的 N N N 个点的亮度大于 I p + T I_p + T Ip+T 或小于 I p − T I_p − T Ip−T ,那么像素 p p p 可以被认为是特征点 ( N N N 通常取 12,即为 FAST-12。其它常用的 N N N 取值为 9 和 11,他们分别被称为 FAST-9, FAST-11)。
- 循环以上四步,对每一个像素执行相同的操作。
- 在 FAST-12 算法中,直接检测邻域圆上的第 1, 5, 9, 13 个像素的亮度。只有当这四个像素中有三个同时大于 I p + T I_p + T Ip+T 或小于 I p − T I_p − T Ip−T 时,当前像素才有可能是一个角点,否则应该直接排除。这样效率更高。同时,在一定区域内仅保留响应极大值的角点,避免角点集中的问题。
- FAST算法的问题:FAST 特征点数量很大且不确定,角点不具有方向信息,尺度弱
- 在ORB中,指定最终要提取的角点数量 N N N,对原始 FAST 角点分别计算 Harris 响应值,然后选取前 N N N 个具有最大响应值的角点,作为最终的角点集合。ORB 添加了尺度和旋转的描述。
- 质心是指以图像块灰度值作为权重的中心。其具体操作步骤如下:
- BRIEF 是一种二进制描述子,它的描述向量由许多个 0 和 1 组成, 0 和 1 编
码了关键点附近两个像素( p p p 和 q q q)的大小关系:如果 p p p 比 q q q 大,则取 1,反之就取 0。若取128个点,则构成128维的0-1向量
7.1.3
- 特征匹配解决了 SLAM 中的数据关联问题,即确定当前看到的路标与之前看到的路标之间的对应关系。
- 由于图像特征的局部特性,误匹配的情况广泛存在,主要原因是因为场景中存在大量重复的纹理。
- 暴力匹配:在图像 I t I_t It 中提取到特征点 x t m , m = 1 , 2 , . . . M x^m_t , m = 1, 2, ... M xtm,m=1,2,...M,在图像 I t + 1 I_{t+1} It+1 中提取到特征点 x t + 1 n , n = 1 , 2 , . . . N x^n_{t+1}, n = 1, 2, ...N xt+1n,n=1,2,...N ,对每一个特征点 x t m x^m_t xtm ,与所有的 x t + 1 n x^n_{t+1} xt+1n 测量描述子的距离,然后排序,取最近的一个作为匹配点。
- 描述子距离表示了两个特征之间的相似程度,对于浮点类型的描述子,使用欧氏距离进行度量,对于二进制的描述子,则采用汉明距离
- 快速近似最近邻(FLANN) 算法更加适合于匹配点数量极多的情况
7.2 实践:特征提取和匹配
7.3 2D-2D: 对极几何
7.3.1 对极约束
- 求取两帧图像 I 1 , I 2 I_1, I_2 I1,I2 之间的运动,设第一帧到第二帧的运动为 R , t \bm{R} ,\bm{t} R,t 。两个相机中心分别为 O 1 , O 2 O_1, O_2 O1,O2 。考虑 I 1 I_1 I1 中有一个特征点 p 1 p_1 p1 ,它在 I 2 I_2 I2 中对应着特征点 p 2 p_2 p2 ,这两个点是同一个空间点在两个成像平面上的投影。连线 O 1 p 1 → \overrightarrow{O_1p_1} O1p1 和连线 O 2 p 2 → \overrightarrow{O_2p_2} O2p2 在三维空间中相交于点 P P P 。点 O 1 , O 2 , P O_1, O_2, P O1,O2,P 三个点确定一个平面,称为极平面, O 1 O 2 O_1O_2 O1O2 连线与像平面 I 1 , I 2 I_1, I_2 I1,I2 的交点分别为 e 1 , e 2 e_1, e_2 e1,e2,称为极点。 O 1 , O 2 O_1, O_2 O1,O2 称为基线 。称极平面与两个像平面 I 1 , I 2 I_1, I_2 I1,I2 之间的相交线 l 1 , l 2 l_1, l_2 l1,l2 为极线。
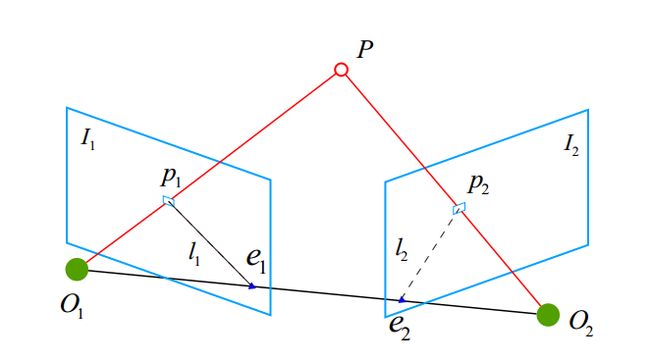
- 对极约束


x 1 , x 2 \bm{x_1}, \bm{x_2} x1,x2 是两个像素点的归一化平面上的坐标, K \bm{K} K 为相机内参矩阵 - 把中间部分记作两个矩阵:基础矩阵 F \bm{F} F 和本质矩阵 E \bm{E} E,可以进一步简化对极约束,实践当中往往使用形式更简单的 E:

对极约束简洁地给出了两个匹配点的空间位置关系 - 由上式,相机位姿估计问题变为以下两步:
- 根据配对点的像素位置,求出 E \bm{E} E 或者 F \bm{F} F
- 根据 E \bm{E} E 或者 F \bm{F} F,求出 R , t \bm{R}, \bm{t} R,t 。
7.3.2 本质矩阵
- E = t ∧ R \bm{E} = \bm{t^{\land}R} E=t∧R 。它是一个 3 × 3 3 × 3 3×3 的矩阵,有 9 个未知数。从 E \bm{E} E 的构造方式上看,有以下值得注意的地方:
- 对极约束是等式为零的约束,所以对 E \bm{E} E 乘以任意非零常数后, 对极约束依然满足,称为 E \bm{E} E 在不同尺度下是等价的
- 本质矩阵 E \bm{E} E 的奇异值必定是 [ σ , σ , 0 ] T [σ, σ, 0]^T [σ,σ,0]T 的形式,称为本质矩阵的内在性质。
- 由于尺度等价性,故 E \bm{E} E 实际上有五个自由度
- 考虑它的尺度等价性,使用八对点来估计 E \bm{E} E ——经典的八点法

其中, u i , v i u^i, v^i ui,vi 表示第 i i i 对特征点,每对特征点的形式是 ( u 1 v 1 ) , ( u 2 , v 2 ) (u_1v_1),(u_2,v_2) (u1v1),(u2,v2), e \bm{e} e向量是本质矩阵 E \bm{E} E 的展开形式。。如果八对匹配点组成的矩阵满足秩为 8 的条件,那么 E \bm{E} E 的各元素就可由上述方程解得。 - 根据已经估得的本质矩阵 E \bm{E} E,恢复出相机的运动 R , t \bm{R}, \bm{t} R,t 。这个过程是由奇异值分解(SVD)得到。

其中 U , V \bm{U}, \bm{V} U,V 为正交阵, Σ \bm{Σ} Σ 为奇异值矩阵,根据 E \bm{E} E 的内在性质,我们知道 Σ = d i a g ( σ , σ , 0 ) \bm{Σ} = diag(σ, σ, 0) Σ=diag(σ,σ,0) - 从 E \bm{E} E 分解到 t , R \bm{t}, \bm{R} t,R 时,一共存在四个可能的解:

只有第一种解中, P P P 在两个相机中都具有正的深度。把任意一点代入四种解中,检测该点在两个相机下的深度,就可以确定哪个解是正确的。 - 根据线性方程解出的 E \bm{E} E,它的奇异值不一定为 σ , σ , 0 σ, σ, 0 σ,σ,0 的形式。刻意地把 Σ \bm{Σ} Σ 矩阵调整成上面的样子。做法是,对八点法求得的 E \bm{E} E 进行 SVD 分解后,会得到奇异值矩阵 Σ = d i a g ( σ 1 , σ 2 , σ 3 ) \bm{Σ} = diag(σ1, σ2, σ3) Σ=diag(σ1,σ2,σ3) ,不妨设 σ 1 ≥ σ 2 ≥ σ 3 σ_1 ≥ σ_2 ≥ σ_3 σ1≥σ2≥σ3 。取:

更简单的做法是将奇异值矩阵取成 d i a g ( 1 , 1 , 0 ) diag(1, 1, 0) diag(1,1,0)
7.3.3 单应矩阵
- 单应描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上(比如墙,地面等),则可以通过单应性来进行运动估计。
- 考虑在图像 I 1 I_1 I1 和 I 2 I_2 I2 有一对匹配好的特征点 p 1 p_1 p1 和 p 2 p_2 p2 ,这些特征点落在某平面上,则有:

得到了一个直接描述图像坐标 p 1 p_1 p1 和 p 2 p_2 p2 之间的变换,把中间这部分记为 H \bm{H} H ,于是

- 自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出,注意,这些特征点不能有三点共线的情况:
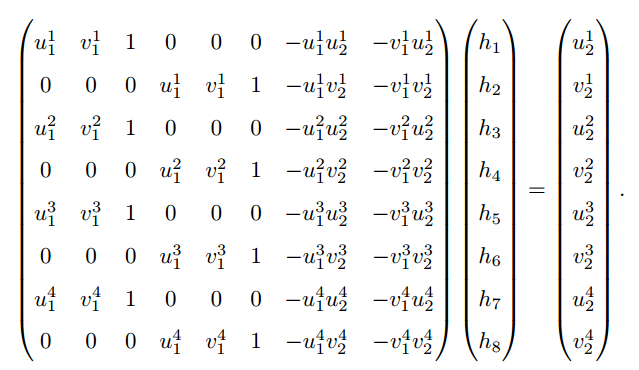
其中,未显示的 h 9 = 1 h_9=1 h9=1。这种做法把 H \bm{H} H 矩阵看成了向量,通过解该向量的线性方程来恢复 H \bm{H} H,又称直接线性变换法。 - 与本质矩阵相似,求出单应矩阵以后需要对其进行分解,才可以得到相应的旋转矩阵 R \bm{R} R 和平移向量 t \bm{t} t 。分解的方法包括数值法与解析法。
- 退化:当特征点共面,或者相机发生纯旋转的时候,基础矩阵的自由度下降。为了能够避免退化现象造成的影响,通常会同时估计基础矩阵 F \bm{F} F 和单应矩阵 H \bm{H} H ,选择重投影误差比较小的那个作为最终的运动估计矩阵。
7.4 实践:对极约束求解相机运动
7.4.1 讨论
- 用 E \bm{E} E 来分解运动时,通常把 t \bm{t} t 进行归一化,让它的长度等于 1。
- 对 t \bm{t} t 长度的归一化,直接导致了单目视觉的尺度不确定性。对两张图像的 t \bm{t} t 归一化,相当于固定了尺度。虽然不知道它的实际长度为多少,但以这时的 t \bm{t} t 为单位 1,计算相机运动和特征点的 3D 位置,这称为单目 SLAM 的初始化。初始化之后的轨迹和地图的单位,就是初始化时固定的尺度,初始化的两张图像必须有一定程度的平移,而后的轨迹和地图都将以此步的
平移为单位。 - 另一种方法是令初始化时所有的特征点平均深度为 1,也可以固定一个尺度。把特征点深度归一化可以控制场景的规模大小,使计算在数值上更稳定
- 从 E \bm{E} E 分解到 R , t \bm{R}, \bm{t} R,t 的过程中,如果相机发生的是纯旋转,导致 t \bm{t} t 为零,则得到的 E \bm{E} E 也将为零,导致无从求解 R \bm{R} R,此时可以依靠 H \bm{H} H 求取旋转,但仅有旋转时,无法用三角测量估计特征点的空间位置。所以单目初始化不能只有纯旋转,必须要有一定程度的平移
- 当给定的点数多于八对时,可以计算最小二乘解:

当可能存在误匹配的情况时,更倾向于使用随机采样一致性。
7.5 三角测量
- 在单目 SLAM 中,仅通过单张图像无法获得像素的深度信息,需要通过三角测量(或三角化)的方法来估计地图点的深度。
- 三角测量是指,通过在两处观察同一个点的夹角,确定该点的距离

如上图,理论上直线 O 1 p 1 O_1p_1 O1p1 与 O 2 p 2 O_2p_2 O2p2 在场景中会相交于一点 P P P,该点即是两个特征点所对应的地图点在三维场景中的位置。然而由于噪声的影响,这两条直线往往无法相交。可以通过最二小乘去求解。 - 按照对极几何中的定义,设 x 1 , x 2 \bm{x_1}, \bm{x_2} x1,x2 为两个特征点的归一化坐标,它们满足:
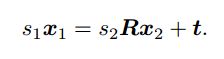
对上式两侧左乘一个 x 1 ∧ \bm{x_1^\land} x1∧ ,得:
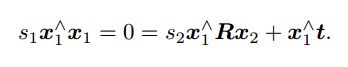
可以根据它直接求得 s 2 s_2 s2 ,继而求得 s 1 s_1 s1。由于噪声的存在,我们估得的 R , t \bm{R}, \bm{t} R,t,不一定精确使上式为零,所以更常见的做法求最小二乘解而不是零解。
7.6 实践:三角测量
- 三角测量是由平移得到的,有平移才会有对极几何中的三角形。
- 当平移很小时,像素上的不确定性将导致较大的深度不确定性,平移较大时,在同样的相机分辨率下,三角化测量将更精确。
- 要增加三角化的精度,其一是提高特征点的提取精度,但会增加成本。另一方式是使平移量增大。但是,平移量增大,会导致图像的外观发生明显的变化,导致匹配失效,这称为三角测量的矛盾。
7.7 3D-2D: PnP
PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。它描述了当知道 n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿,3D-2D 方法不需要使用对极约束,又可以在很少的匹配点中获得较好的运动估计
7.7.1 直接线性变换
- 考虑某个空间点 P P P,它的齐次坐标为 P = ( X , Y , Z , 1 ) T \bm{P} = (X, Y, Z, 1)^T P=(X,Y,Z,1)T。在图像 I 1 I_1 I1 中,投影到特征
点 x 1 = ( u 1 , v 1 , 1 ) T \bm{x_1} = (u_1, v_1, 1)^T x1=(u1,v1,1)T(以归一化平面齐次坐标表示)。此时相机的位姿 R , t \bm{R},\bm{t} R,t 是未知的。与单应矩阵的求解类似,我们定义增广矩阵 [ R ∣ t ] [\bm{R}|\bm{t}] [R∣t] 为一个 3 × 4 3 × 4 3×4 的矩阵,包含了旋转与平移信息
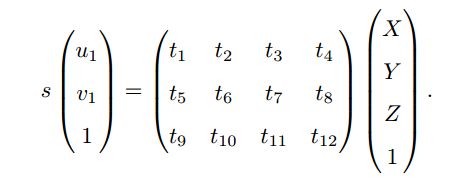
- 定义 T \bm{T} T 的行向量:

假设一共有 N N N 个特征点,可以列出线性方程组:
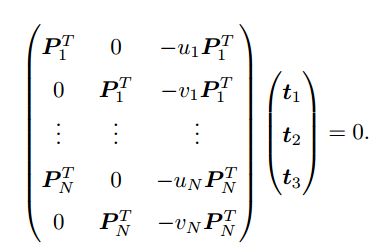
由于 t \bm{t} t 一共有 12 维,因此最少通过六对匹配点,即可实现矩阵 T \bm{T} T 的线性求解,这种方法(也)称为直接线性变换。当匹配点大于六对时,可以使用 SVD 等方法对超定方程求最小二乘解。
7.7.2 P3P
- P3P仅使用三对匹配点,对数据要求较少,它的输入数据为三对 3D-2D 匹配点,此外, P3P 还需要使用一对验证点,以从可能的解出选出正确的那一个(类似于对极几何情形)。记验证点对为 D − d D − d D−d ,相机光心为 O O O 。

- 根据余弦定理:

对上面三式全体除以 O C 2 OC^2 OC2,并且记 x = O A / O C , y = O B / O C x = OA/OC, y = OB/OC x=OA/OC,y=OB/OC ,得
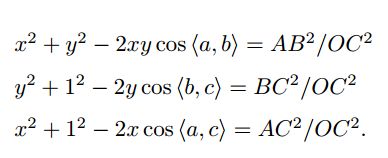
记 v = A B 2 / O C 2 , u v = B C 2 / O C 2 ; w v = A C 2 / O C 2 v = AB^2/OC^2, uv = BC^2/OC^2; wv = AC^2/OC^2 v=AB2/OC2,uv=BC2/OC2;wv=AC2/OC2 ,有:

该方程组是关于 x , y x, y x,y 的一个二元二次方程 - P3P最后把问题转化为一个3D-3D的问题,然而, P3P 也存在着一些问题:
- P3P 只利用三个点的信息。当给定的配对点多于 3 组时,难以利用更多的信息
- 如果 3D 点或 2D 点受噪声影响,或者存在误匹配,则算法失效