用python进行碰撞动力学仿真

问题阐述

A,B两球在同一平面里，A球有一初速度，B球无初速度，一段时间后两球发生碰撞。
两球碰撞时接触力模型假设：


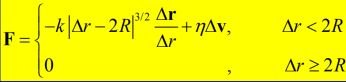
数值仿真：

（R为两球的半径，mA为A球质量，mB为B球质量，rA0为A球的初始位置，VA0为A球的初始速度，rB0为B球的初始位置，VB0为B球的初始速度。）

解题过程

解题思路

（1）两球之间的的距离r可以根据勾股定理求得。
（2）①当r>=2R时，两者间无作用力，各自的位置等于ri+v(i+1)dt。②当r<2R时，可以根据公式计算出它们间的作用力Fi，对于A为Fi，对于B为-Fi。根 据动量定理可得v(i+1)=Fidt/m+vi，r(i+1)=ri+v(i+1)*dt。
（3）作图。

程序编写

运用改进欧拉法来进行数值积分。
首先引入库。

from numpy import*
import matplotlib.pyplot as plt #引入库

参数初始化。

R = 0.02
ma = 0.1
mb = 0.1
k = 20000
df = 1.0
time = 0.1
dt = 0.0001 #设置数值

n = int(time/dt)
t = zeros(n,float)
ra = zeros((n,2),float)
rb = zeros((n,2),float)
va = zeros((n,2),float)
vb = zeros((n,2),float)
f = zeros((n,2),float)  #设置数值

ra[0] = array([0.0,0.0])
rb[0] = array([0.08,0.018])
va[0] = array([1.0,0.0])
vb[0] = array([0.0,0.0])  #初始化

因为是二维的，所以用向量来进行计算。
进行数值积分。

for i in range(n-1):
    dr = sqrt((ra[i][0] - rb[i][0])**2+(ra[i][1]-rb[i][1])**2)
    if dr >= 2*R:
        f[i] = 0 
        va[i+1] = va[i]
        vb[i+1] = vb[i] #r>=2R时
    else:
        f[i] = -k*(abs(dr - 2*R))**(3/2)*(rb[i]-ra[i])/dr + df*(vb[i]-va[i])
        va[i+1] = f[i]*dt/ma + va[i]
        vb[i+1] = -f[i]*dt/mb + vb[i] #r<2R时
    ra[i+1] = ra[i] + va[i+1]*dt
    rb[i+1] = rb[i] + vb[i+1]*dt
    t[i+1] = t[i] + dt  

得到球A和B的位置坐标，和速度x，y方向的分量。
最后作图。

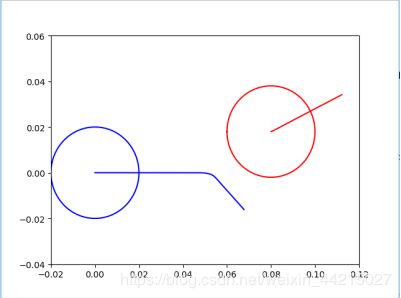
th = linspace(-pi,pi,100)
plt.plot(ra[:,0],ra[:,1],"-b",R*cos(th),R*sin(th),"-b",rb[:,0],rb[:,1],"-r",0.08+R*cos(th),0.018+R*sin(th),"-r")
plt.axis([-0.02,0.12,-0.04,0.06])
plt.show()  #画两球在平面上的轨迹

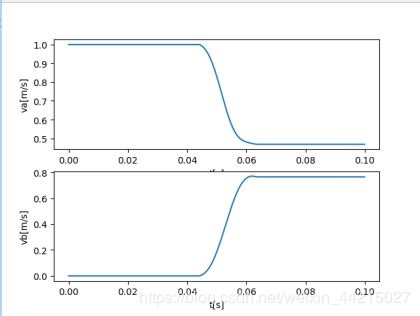
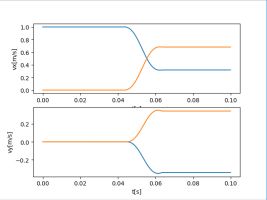
plt.subplot(211)
plt.plot(t,sqrt(va[:,0]**2+va[:,1]**2))
plt.xlabel("t[s]")
plt.ylabel("va[m/s]")
plt.subplot(212)
plt.plot(t,sqrt(vb[:,0]**2+vb[:,1]**2))
plt.xlabel("t[s]")
plt.ylabel("vb[m/s]")
plt.show()  #画出两球的速度随时间的变化

延伸扩展

改变η来观察两球碰撞结果（以动画来展示）。

from numpy import*
import matplotlib.pyplot as plt
import matplotlib.animation as an  #引入库

def norm(df):
    R = 0.02
    ma = 0.1
    mb = 0.1
    k = 20000
    #df = 1.0
    time = 0.1
    dt = 0.0001 #设置数值

    n = int(time/dt)
    t = zeros(n,float)
    ra = zeros((n,2),float)
    rb = zeros((n,2),float)
    va = zeros((n,2),float)
    vb = zeros((n,2),float)
    f = zeros((n,2),float)  #设置数值

    ra[0] = array([0.0,0.0])
    rb[0] = array([0.08,0.018])
    va[0] = array([1.0,0.0])
    vb[0] = array([0.0,0.0])  #初始化

    for i in range(n-1):
        dr = sqrt((ra[i][0] - rb[i][0])**2+(ra[i][1]-rb[i][1])**2)
        if dr >= 2*R:
            f[i] = 0 
            va[i+1] = va[i]
            vb[i+1] = vb[i]
            ra[i+1] = ra[i] + va[i+1]*dt
            rb[i+1] = rb[i] + vb[i+1]*dt
            t[i+1] = t[i] + dt  #r>=2R时
        else:
            f[i] = -k*(abs(dr - 2*R))**(3/2)*(rb[i]-ra[i])/dr + df*(vb[i]-va[i])
            va[i+1] = f[i]*dt/ma + va[i]
            vb[i+1] = -f[i]*dt/mb + vb[i]
            ra[i+1] = ra[i] + va[i+1]*dt
            rb[i+1] = rb[i] + vb[i+1]*dt
            t[i+1] = t[i] + dt  #r<2R时
            
    return ra,rb

将数值积分写成一个函数，传入的参数为η。
然后分别做A和B的动画。
A球的轨迹动画

s = linspace(0,3,100)  #改变η的大小。
ra,rb = norm(0)
fig = plt.figure()
line, = fig.add_subplot(111).plot(ra[:,0],ra[:,1])

def init():
    line.set_data([],[])
    return line,

def updata(data):
    line.set_data(norm(data)[0][:,0],norm(data)[0][:,1])
    return line,

ani = an.FuncAnimation(fig,updata,frames=s,init_func=init,interval = 50,blit=False)
plt.savefig("a.png")
plt.show()  #A球的轨迹动画

B球的轨迹动画

s = linspace(0,3,100) #改变η的大小。
ra,rb = norm(0)
fig = plt.figure()
line, = fig.add_subplot(111).plot(rb[:,0],rb[:,1])

def init():
    line.set_data([],[])
    return line,

def updata(data):
    line.set_data(norm(data)[1][:,0],norm(data)[1][:,1])
    return line,

ani = an.FuncAnimation(fig,updata,frames=s,init_func=init,interval = 50,blit=False)
plt.savefig("a.png")
plt.show()  #B球的轨迹动画

讨论
当η=0时，为弹性碰撞。
①对心碰撞：

此时，A与B交换了速度。动量守恒，能量守恒。
②非对心碰撞：

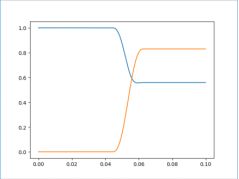
其y方向速度矢量和为零，x方向矢量和等于之前的。

当η！= 0时，为非弹性碰撞。（η=1.0）
①对心碰撞：

此时，动量守恒，但是能量会有损失。
②非对心碰撞：

y方向矢量和为零，x方向矢量和等于之前的。能量损失。

结语

python可以干很多我们不能做到的事，只要模型能够建立，我们就能模拟出它的过程。