原文见https://datascienceplus.com/proteomics-data-analysis-2-3-data-filtering-and-missing-value-imputation/
Proteomics Data Analysis (2/3): Data Filtering and Missing Value Imputation
Published on August 28, 2018 at 8:36 am
Welcome to Part Two of the three-part tutorial series on proteomics data analysis. The ultimate goal of this exercise is to identify proteins whose abundance is different bewteen the drug-resistant cells and the control. In other words, we are looking for a list of differentially regulated proteins that may shed light on how cells escape the cancer-killing action of a drug. In Part One, I have demonstrated the steps to acquiring a proteomics data set and performing data pre-processing. We will pick up from the cleaned data set and confront the missing value problem in proteomics.
Again, the outline for this tutorial series is as follows:
- Data acquisition and cleaning
- Data filtering and missing value imputation
- Statistical testing and data interpretation
Missing Value Problem
Although mass spectrometry-based proteomics has the advantage of detecting thousands of proteins from a single experiment, it faces certain challenges. One problem is the presence of missing values in proteomics data. To illustrate this, let's examine the first few rows of the log2-transformed and raw protein abundance values.
library(dplyr)
head(select(df, Gene, starts_with("LOG2")))
## Gene LOG2.Parental_bR1 LOG2.Parental_bR2 LOG2.Parental_bR3
## 1 RBM47 -Inf -Inf 21.87748
## 2 ESYT2 25.6019 25.56180 25.68763
## 3 ILVBL -Inf 20.76474 -Inf
## 4 KLRG2 -Inf -Inf 22.31786
## 5 CNOT1 -Inf -Inf -Inf
## 6 PGP -Inf -Inf -Inf
## LOG2.Resistant_bR1 LOG2.Resistant_bR2 LOG2.Resistant_bR3
## 1 -Inf -Inf -Inf
## 2 -Inf -Inf -Inf
## 3 -Inf -Inf -Inf
## 4 -Inf -Inf -Inf
## 5 -Inf -Inf 29.14207
## 6 -Inf -Inf 22.46269
head(select(df, Gene, starts_with("LFQ")))
## Gene LFQ.intensity.Parental_bR1 LFQ.intensity.Parental_bR2
## 1 RBM47 0 0
## 2 ESYT2 50926000 49530000
## 3 ILVBL 0 1781600
## 4 KLRG2 0 0
## 5 CNOT1 0 0
## 6 PGP 0 0
## LFQ.intensity.Parental_bR3 LFQ.intensity.Resistant_bR1
## 1 3852800 0
## 2 54044000 0
## 3 0 0
## 4 5228100 0
## 5 0 0
## 6 0 0
## LFQ.intensity.Resistant_bR2 LFQ.intensity.Resistant_bR3
## 1 0 0
## 2 0 0
## 3 0 0
## 4 0 0
## 5 0 592430000
## 6 0 5780200
It is hard to miss the -Inf, which represent protein intensity measurements of 0 in the raw data set. We consider these data points as missing values, or a lack of quantification in the indicated samples. This is a common issue in proteomics experiments, and it arises due to sample complexity and randomness (or stochasticity) in sampling.
For example, imagine pouring out a bowl of Lucky Charms cereal containing a thousand different marshmallows. Let's say there is only one coveted rainbow marshmallow for every one thousand pieces. The likelihood of your bowl containing the rare shape is disappointingly low. In our situation, there are approximately 20,000 proteins expressed in a given cell, and many in low quantities. Hence, the probability of consistently capturing proteins with low expression across all experiments is small.
Data Filtering
To overcome the missing value problem, we need to remove proteins that are sparsely quantified. The hypothesis is that a protein quantified in only one out of six samples offers insufficient grounds for comparison. In addition, the protein could have been mis-assigned.
One of many filtering schemes is to keep proteins that are quantified in at least two out of three replicates in one condition. To jog your memory, we have two conditions, one drug-resistant cell line and a control, and three replicates each. The significance of replicates will be discussed in Part 3 of the tutorial. For now, we will briefly clean the data frame and apply filtering.
## Data cleaning: Extract columns of interest
df = select(df, Protein, Gene, Protein.name, starts_with("LFQ"), starts_with("LOG2"))
glimpse(df)
## Observations: 1,747
## Variables: 15
## $ Protein "A0AV96", "A0FGR8", "A1L0T0", "A4D...
## $ Gene "RBM47", "ESYT2", "ILVBL", "KLRG2"...
## $ Protein.name "RNA-binding protein 47", "Extende...
## $ LFQ.intensity.Parental_bR1 0, 50926000, 0, 0, 0, 0, 0, 0, 0, ...
## $ LFQ.intensity.Parental_bR2 0, 49530000, 1781600, 0, 0, 0, 0, ...
## $ LFQ.intensity.Parental_bR3 3852800, 54044000, 0, 5228100, 0, ...
## $ LFQ.intensity.Resistant_bR1 0, 0, 0, 0, 0, 0, 0, 0, 0, 8213400...
## $ LFQ.intensity.Resistant_bR2 0, 0, 0, 0, 0, 0, 0, 0, 0, 6903700...
## $ LFQ.intensity.Resistant_bR3 0, 0, 0, 0, 592430000, 5780200, 0,...
## $ LOG2.Parental_bR1 -Inf, 25.60190, -Inf, -Inf, -Inf, ...
## $ LOG2.Parental_bR2 -Inf, 25.56180, 20.76474, -Inf, -I...
## $ LOG2.Parental_bR3 21.87748, 25.68763, -Inf, 22.31786...
## $ LOG2.Resistant_bR1 -Inf, -Inf, -Inf, -Inf, -Inf, -Inf...
## $ LOG2.Resistant_bR2 -Inf, -Inf, -Inf, -Inf, -Inf, -Inf...
## $ LOG2.Resistant_bR3 -Inf, -Inf, -Inf, -Inf, 29.14207, ...
## Data filtering function
filter_valids = function(df, conditions, min_count, at_least_one = FALSE) {
# df = data frame containing LOG2 data for filtering and organized by data type
# conditions = a character vector dictating the grouping
# min_count = a numeric vector of the same length as "conditions" indicating the minimum
# number of valid values for each condition for retention
# at_least_one = TRUE means to keep the row if min_count is met for at least one condition
# FALSE means min_count must be met across all conditions for retention
log2.names = grep("^LOG2", names(df), value = TRUE) # Extract LOG2 column names
cond.names = lapply(conditions, # Group column names by conditions
function(x) grep(x, log2.names, value = TRUE, perl = TRUE))
cond.filter = sapply(1:length(cond.names), function(i) {
df2 = df[cond.names[[i]]] # Extract columns of interest
df2 = as.matrix(df2) # Cast as matrix for the following command
sums = rowSums(is.finite(df2)) # count the number of valid values for each condition
sums >= min_count[i] # Calculates whether min_count requirement is met
})
if (at_least_one) {
df$KEEP = apply(cond.filter, 1, any)
} else {
df$KEEP = apply(cond.filter, 1, all)
}
return(df) # No rows are omitted, filter rules are listed in the KEEP column
}
## Apply filtering
df.F = filter_valids(df,
conditions = c("Parental", "Resistant"),
min_count = c(2, 2),
at_least_one = TRUE)
The output data frame df.F is a copy of df with an additional KEEP column indicating the rows to retain. We will complete the filtering using the following operation and then check out the first couple of rows.
df.F = filter(df.F, KEEP)
head(select(df.F, Gene, starts_with("LOG2")))
## Gene LOG2.Parental_bR1 LOG2.Parental_bR2 LOG2.Parental_bR3
## 1 ESYT2 25.60190 25.56180 25.68763
## 2 EIF3C 26.93022 27.11644 26.83231
## 3 NACAM 27.71299 27.66756 27.53527
## 4 DX39A 25.90933 25.69806 25.93283
## 5 BACH 25.07153 25.39110 25.06027
## 6 MYO1C 27.16471 27.48416 27.43841
## LOG2.Resistant_bR1 LOG2.Resistant_bR2 LOG2.Resistant_bR3
## 1 -Inf -Inf -Inf
## 2 26.29148 26.04087 26.46083
## 3 29.03570 28.68295 28.89753
## 4 26.39331 26.54022 -Inf
## 5 -Inf -Inf -Inf
## 6 27.61400 27.02263 27.44530
Notice that the protein in the first row is quantified in the Parental line but not the Resistant one. Proteins like this are of great interest to us as they are likely implicated in the mechanism of drug resistance. In addition, note that the final number of proteins after filtering (1031) is roughly 60% the original number (1747). Filtering reduces our list of proteins to ones quantified in a reasonably consistent manner.
Data Normalization
Before we proceed to imputation, we need to account for technical variability in the amount of sample analyzed by the mass spectrometer from one run to another. This is an issue parallel to the variation in sequencing depth in RNAseq experiments. To normalize out these technical differences, we performed a global median normalization. For each sample, the median of the log2-transformed distribution is subtracted from all the values.
## Data normalization function
median_centering = function(df) {
# df = data frame containing LOG2 columns for normalization
LOG2.names = grep("^LOG2", names(df), value = TRUE)
df[, LOG2.names] = lapply(LOG2.names,
function(x) {
LOG2 = df[[x]]
LOG2[!is.finite(LOG2)] = NA # Exclude missing values from median calculation
gMedian = median(LOG2, na.rm = TRUE)
LOG2 - gMedian
}
)
return(df)
}
## Normalize data
df.FN = median_centering(df.F)
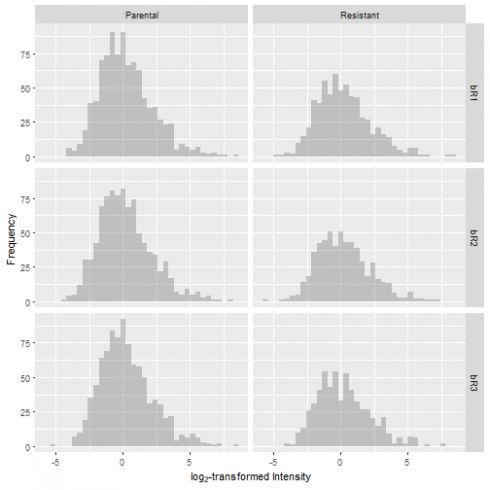
The result is that each sample is centered at a log2(intensity) of 0.
Data Imputation
After filtering and normalization, some missing values remain. How do we deal with them from here? The statistical approach designed to answer such a question is called imputation. For a thorough discussion of imputation on proteomics data sets, I highly recommend this article in the Journal of Proteome Research.
Since missing values are associated with proteins with low levels of expression, we can substitute the missing values with numbers that are considered “small” in each sample. We can define this statistically by drawing from a normal distribution with a mean that is down-shifted from the sample mean and a standard deviation that is a fraction of the standard deviation of the sample distribution. Here's a function that implements this approach:
## Data imputation function
impute_data = function(df, width = 0.3, downshift = 1.8) {
# df = data frame containing filtered
# Assumes missing data (in df) follows a narrowed and downshifted normal distribution
# use_keep = filter rows using KEEP column prior to imputation
LOG2.names = grep("^LOG2", names(df), value = TRUE)
impute.names = sub("^LOG2", "impute", LOG2.names)
# Create new columns indicating whether the values are imputed
df[impute.names] = lapply(LOG2.names, function(x) !is.finite(df[, x]))
# Imputation
set.seed(1)
df[LOG2.names] = lapply(LOG2.names,
function(x) {
temp = df[[x]]
temp[!is.finite(temp)] = NA
temp.sd = width * sd(temp[df$KEEP], na.rm = TRUE) # shrink sd width
temp.mean = mean(temp[df$KEEP], na.rm = TRUE) -
downshift * sd(temp[df$KEEP], na.rm = TRUE) # shift mean of imputed values
n.missing = sum(is.na(temp))
temp[is.na(temp)] = rnorm(n.missing, mean = temp.mean, sd = temp.sd)
return(temp)
})
return(df)
}
## Apply imputation
df.FNI = impute_data(df.FN)
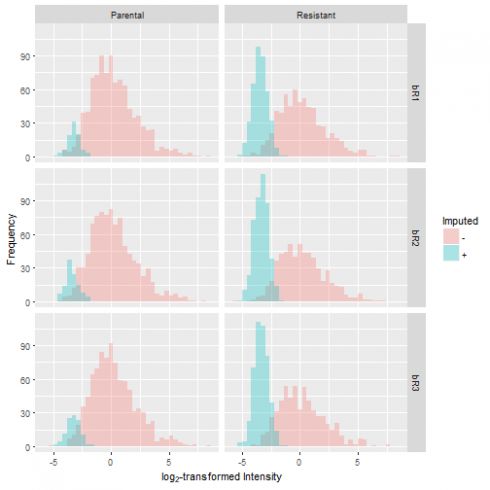
Let's graphically evaluate the results by overlaying the distribution of the imputed values over the original distribution. In doing so, we observe that the number of missing values is greater in the resistant condition compared to the control. Furthermore, the missing values take on a narrow spread at the lower end of the sample distribution, which reflects our notion that low levels of protein expression produce missing data.
Summary
This is the second of three tutorials on proteomics data analysis. I have described the approach to handling the missing value problem in proteomics.
In the final tutorial, we are ready to compare protein expression between the drug-resistant and the control lines. This involves performing a two-sample Welch's t-test on our data to extract proteins that are differentially expressed. Moreover, we will discuss ways to interpret the final output of a high-throughput proteomics experiment. Stay tuned for the revelation of proteins that may play a role in driving the resistance of tumor cells.