数据结构详解——堆

数据结构详解——堆

堆的定义

首先我们给出最大树（最小树）的定义：

最大树（最小树）是一棵有向树，其中每个节点的值都大于（小于）或等于它的孩子结点的值。

可以看出，最大树（最小树）不一定是二叉树，下面给出最大树的例子：

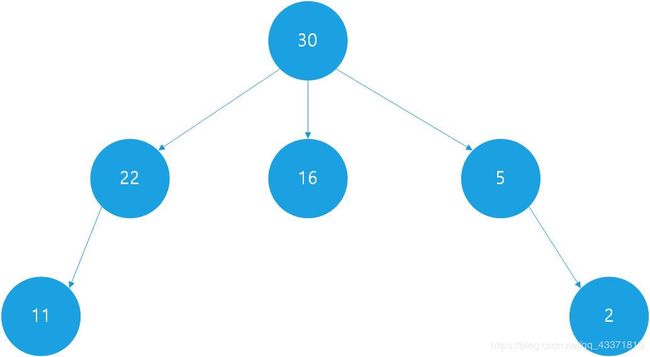
由此我们可以得到堆的定义：

最大堆（最小堆）是一棵最大（最小）树，同时它也是一棵完全二叉树。

最大堆的例子：

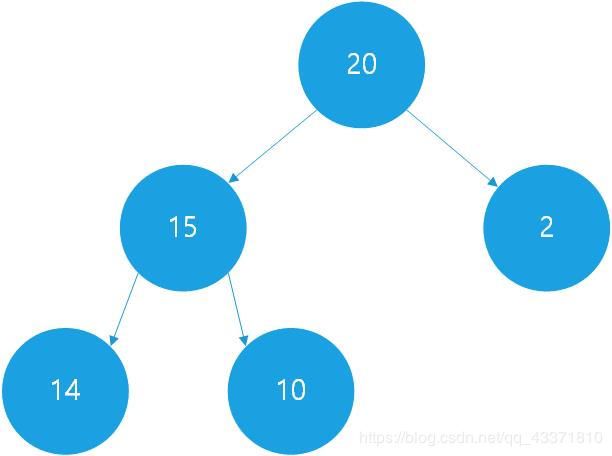
根据堆是完全二叉树的特性，我们完全可以使用线性表来表示这个树，每个元素在线性表中的位置即为它们在满二叉树中的编号。

在上面的图中，20对应线性表1号位置，15对应2号，2对应3号，14对应4号，10对应5号。从中不难看出，堆有一些重要的性质：

• 左孩子的编号一定等于它父亲节点编号的两倍，右孩子的编号一定等于它父亲节点编号的两倍再加一。
• 堆的每一个子树都是堆。

堆的作用

堆实际上是为了方便地实现一类数据结构——优先级队列。与我们一般熟悉的先进先出（FIFO）的队列不同，优先级队列每次出队列的元素一定是优先级最高（或最低）的元素，入队列时也要根据优先级安排位置，这两类分别对应了最大优先级队列和最小优先级队列，最大优先级队列用抽象数据类型表示如下：

	AbstractDataType MaxPriorityQueue
	{
		实例：
			元素的优先集合，每个元素都有一个优先级。
		操作：
			isEmpty():如果队列为空则返回True;
			getMax():返回队列中的元素个数;
			put(x):将元素x插入队列;
			removeMax():从队列中删除具有最大优先级的元素，并返回该元素;
	｝

最小优先级队列与最大优先级队列恰好相反，但实现方案是一样的，因此下面我们只讨论最大优先级队列。

另外，应用堆，还可以实现一个时间复杂度为$O(nlogn)$的排序算法——堆排序。

堆操作及Java语言实现

根据前面的抽象数据类型，我们首先定义一个优先级队列接口：

/**
 * 优先级队列
 */
public interface PriorityQueue {
    boolean isEmpty();//队列为空返回True
    int size();//返回队列长度
    void put(Comparable theObject);//插入元素
}

然后定义一个最大优先级队列接口，该接口继承优先级队列接口。

/**
 * 最大优先级队列
 */
public interface MaxPriorityQueue extends PriorityQueue{
    Comparable getMax();//返回最大元素
    Comparable removeMax();//去除优先级最大的元素
}

这里我们用泛型的方法，将元素类型定义为Java内置的Comparable类型，该接口的实现类需要实现compareTo()方法，我们在比较元素时，就需要使用compareTo()方法。这样可以实现队列中元素类型可变。

接下来用一个MaxHeap类实现MaxPriorityQueue接口，并依次重写接口中的方法即可。

元素的优先集合

对于堆来说，我们需要一个类似线性表的结构来存储每个节点的信息，我们利用Java提供的ArrayList类来进行处理，并提供两个构造函数和一个获取长度的方法：

public class MaxHeap implements MaxPriorityQueue{

    private ArrayList<Comparable> heap;//元素列表
    
    public MaxHeap(){
        heap = new ArrayList<>();
    }

    public MaxHeap(int initLength){
        heap = new ArrayList<>(initLength);
    }

	@Override
    public int size() {
        return this.heap.size();
    }
}

取得优先级最大的元素

根据堆的定义，不难看出堆的第一个元素就是优先级最大的元素，因此将列表中0位置的元素返回即可。代码如下：

    @Override
    public boolean isEmpty() {
        if (heap.size() == 0) return true;
        else return false;
    }

插入元素到最大堆

下面举例说明如何插入一个元素到最大堆中，假设我们已有一个如下图所示的最大堆：

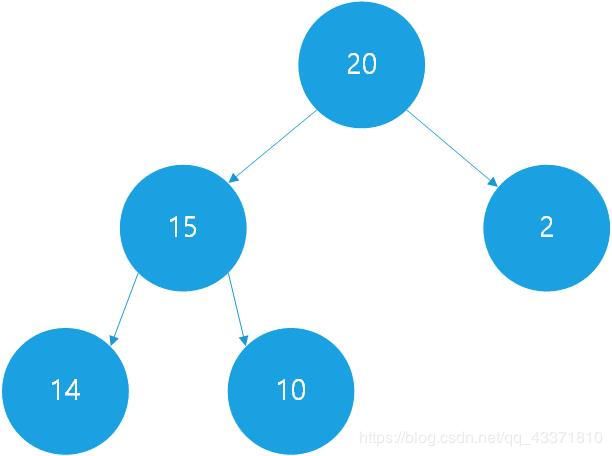
我们现在要插入一个大小为8的节点，首先考虑插入后的完全二叉树的结构：

因此我们先将8这个节点放到最后一个位置，然后向上冒泡：和父亲节点的值比较，父亲节点值较小就交换两个节点的值，直到不能交换或者到根节点。

Java实现如下：

	@Override
    public void put(Comparable theObject) {
        heap.add(theObject);
        int currentNode = heap.size();
        while (currentNode != 1 && heap.get(currentNode/2 - 1).compareTo(theObject) < 0){
            heap.set(currentNode - 1,heap.get(currentNode/2 - 1));
            currentNode = currentNode / 2;
        }
        heap.set(currentNode - 1,theObject);
    }

从最大堆中删除元素

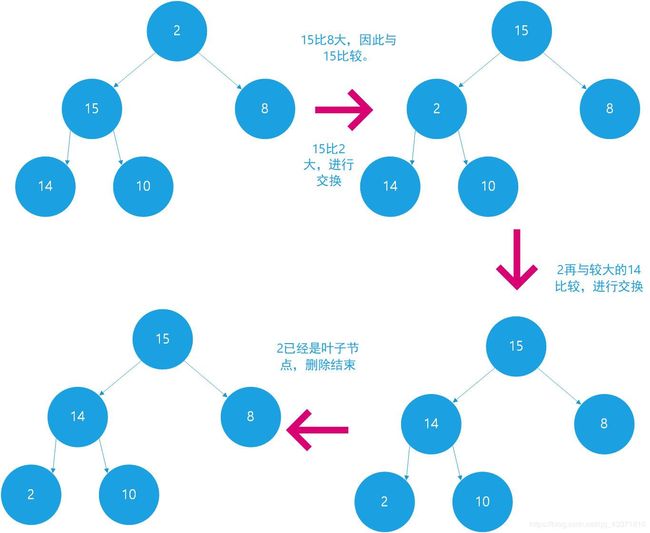
我们已经知道，最大堆中优先级最高的元素就是根节点，所以从最大堆中删除元素时，是从根节点开始的。假设我们有这样一个最大堆：

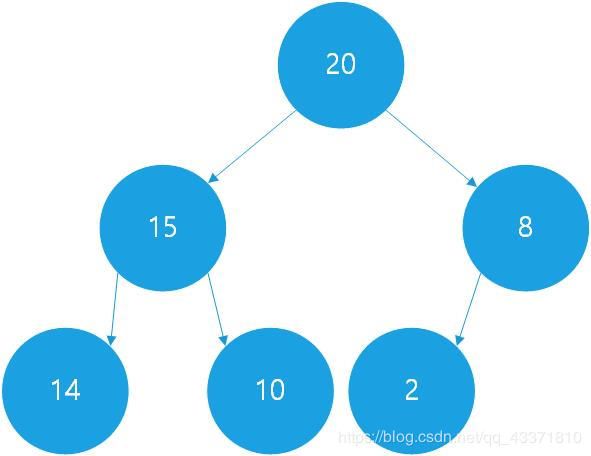
我们要删除的元素是最大的元素20，考虑删除后的完全二叉树结构：

需要删除的不是根节点而是编号最大的节点，因此我们要将最后一个节点取出，然后把这个节点值放在根节点处，从根节点开始，向下冒泡：跟它的孩子节点值比较，若孩子节点值较大就交换，否则固定该节点的位置，删除操作结束。需要注意的是在每次比较前，首先要比较两个孩子的大小，选取其中最大的再跟父亲节点比较。

代码实现如下：

    @Override
    public Comparable removeMax() {
        if (heap.size() == 0) return null;
        Comparable maxElem = heap.get(0);//记录最大结点，用于返回
        //去除最后一个元素，然后再将这个元素插入堆
        Comparable lastElem = heap.get(heap.size() - 1);
        heap.remove(heap.size() - 1);
        if (size() == 0) return maxElem;
        int currentNode = 1,child = 2;
        while (child <= heap.size()){
            //如果右子树比左子树大，转向右子树
            if (child < heap.size() && heap.get(child - 1).compareTo(heap.get(child)) < 0){
                child++;
            }
            //如果最后一个元素比它左右子树都大，则将该元素插入即可
            if (lastElem.compareTo(heap.get(child - 1)) >= 0){
                break;
            }
            heap.set(currentNode - 1,heap.get(child - 1));
            currentNode = child;
            child *= 2;
        }
        heap.set(currentNode - 1,lastElem);
        return maxElem;
    }

堆的应用——堆排序

堆的一个非常重要的应用就是堆排序。它的基本思想就是首先将一个数组构造成一个堆，然后不断地弹出它优先级最大的元素，然后再用上面讲的删除元素的方法重新构造堆，再取优先级最大的元素……直到堆变为空。这样就可以得到一个从大到小的序列。

具体代码实现如下，首先我们在堆这一数据结构中加入一个直接由Comparable数组构造堆的构造方法，在构造方法中我们只需要把所有元素依次调用插入方法即可：

    public MaxHeap(@NotNull Comparable[] theHeap){
        heap = new ArrayList<>();
        for (Comparable elem : theHeap){
            put(elem);
        }
    }

然后在排序工具类中定义堆排序的静态方法HeapSort，传入Comparable数组并对其构造堆，用堆排序的方法进行排序。

    @NotNull
    public static void heapSort(Comparable[] theList, int theSize){
        MaxHeap maxHeap = new MaxHeap(theList);
        for (int i = 0;i < theSize;i++){
            theList[i] = maxHeap.removeMax();
        }
    }