2020牛客暑期多校训练营K-Bag(离散化，集合交+前缀和/滑动窗口+枚举)

K-Bag

题目描述

输入描述:

输出描述:

示例1

输入

1
8 3
2 3 2 1 3 3 2 1

输出

YES

题目大意

定义一个数列叫做$k-bag$当且仅当这个数列是由$1\sim k$的排列组成的。
例如，数列$1,2,3,2,3,1,1,3,2$是一个$3-bag$。
题目要求你判断一个数列是不是$k-bag$的一部分($part-k-bag$)。

分析

以下以样例为例。
$2,3,2,1,3,3,2,1$中，可以发现在前面补一个1就可以构成$k-bag$，所以这是个$part-k-bag$。那么我们是怎么想的呢，是枚举了分割点，然后向后$k$位，再设置一个分割点。最后检验是否可行即可。但是显然，这种方式是超时的，那么考虑优化，在枚举的时候，发现分割点总是在两个相同的数之间，比如第一位的$2$和第三位的$2$之间肯定是有一个分割点。

由此，我们可以扫一遍，遇到一个端点相同的区间就判断是否与之前矛盾即可。那么问题是怎么判断矛盾。我们枚举的区间是可以设置分割点的区间，而分割点是每隔$k$个数有一个的，因此我们可以把这个区间向前移动$a\ast k$格是一样的，由此，可以把所有的区间以$k$为步长向前移动直到与其他区间有交集为止。如果没有交集那么就是不合法的。

很快就WA了，因为有如下这种情况。

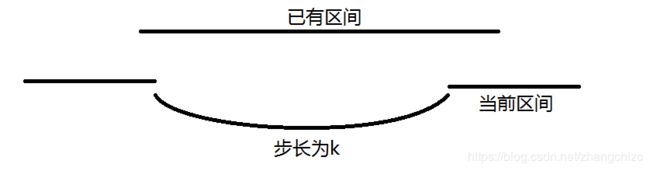
那么两边的交集都是要维护的，因此只维护左右端点是不够的。此时，需要用到一个技巧，前缀和。

我们可以将一个区间的左端点+1，右端点右边的位置-1，然后求前缀和，发现每个位置的数值就是重叠在上面区间的个数，最后找一下有没有数值是等于区间数的就可以了。

具体实现见代码。

还有一点，就是因为$k$太大了，如果超过了$n$就需要用到离散化。

代码

#include
#define ll long long
using namespace std;
const int MAXN=5e5+10;
int a[MAXN],b[MAXN],pre[MAXN],lap[MAXN];
int n,k;
void lsh(){
    sort(b+1,b+1+n); int cnt=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+1+cnt,a[i])-b;
}//离散化成下标，unique是去重函数，对已经排序的数组去重，
//并返回去重后的长度的地址，减去数组名就是去重后的长度了。
int main()
{
	int T;scanf("%d",&T);
	while(T--){
		bool fl=1;
		scanf("%d%d",&n,&k);
		for(int i=1;i<=n;i++){
			scanf("%d",&a[i]),b[i]=a[i];
			if(a[i]>k) fl=0; 
		}
		if(!fl){puts("NO");continue;}//如果有数据大于k，显然不合法
		if(k>n) lsh();
		memset(lap,0,sizeof(lap));//last pos，lap[i]表示i在上一次出现的位置
		memset(pre,0,sizeof(pre));//前缀数组
		int QAQ=0;//是不是眼熟，表示区间个数
		for(int i=1;i<=n;i++){
			if(lap[a[i]]&&lap[a[i]]>i-k){//只有当区间大于k的时候才要处理，否则必定能够覆盖已有的区间
				QAQ++;
				if(lap[a[i]]%k<i%k){
					pre[lap[a[i]]%k]++;
					pre[i%k]--;
				}//如果没有出现分析中的bug
				else{
					pre[lap[a[i]]%k]++;
					pre[i%k]--;
					pre[0]++;
					pre[min(k,n+1)]--;
				}//如果出现了bug
			}lap[a[i]]=i;//把lap更新
		}fl=0;
		for(int i=0;i<min(k,n+1);i++){
			if(i) pre[i]+=pre[i-1];//前缀
			if(pre[i]==QAQ){fl=1;break;}//如果有前缀，即区间个数等于QAQ，那么是合法
		}
		printf(fl?"YES\n":"NO\n");
	}
}

END

调了整整6个小时的bug。