一般的,对正余弦信号进行採样并DFT运算,画出频谱图,会发现频谱并不干净。这样的现象称为频谱泄漏。由于DFT运算仅仅能是有限序列,突然的截断产生了泄漏。
会有这种特殊情况。当採样截取的刚好是整数个周期,则频谱图显得特别干净。
能够理解为刚好取的完整周期。周期性明显了,频率就比較单一。
为此做了matlab实验:
ts = 0.01;%採样率100Hz
n = 0:N-1;
y = sin(2*pi*20*n*ts);%20Hz信号,每周期採5个点
xk = abs(fft(y,N));%注意依据fft算法,这里的N和序列长度N是一样的
stem(xk);
当N = 20、22、24、25时的频谱:
由于20和25是5的倍数。取的周期是完整的。所以频谱是干净的。这就是所谓的特殊情况。
但一般的,取不到完整的周期,频谱泄漏是避免不了的。并且泄露的严重了会影响分辨能力。那么接下来的问题是,怎么提高分辨力?
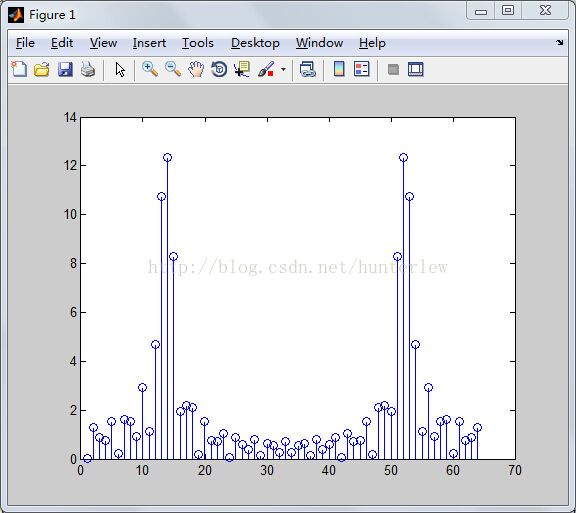
我们试一试採样点数,同一时候FFT点数也添加了。当N=64时的频谱:
通常DFT点数能够添加。採样点数添加不了。于是我们有了补零的方法。
以上面的样例为例。还是64点DFT,可是n是0:24,后面的补零,即 y = [sin(2*pi*20*n*ts),zeros(1,39)];补到64个点。这样得到的频谱是:
我们再取高的点数。当採样点数等于DFT点数等于1024时的频谱:
当採样点数靠补零的方法补到1024个点的频谱:
因此我们得到重要结论:
为了使得频谱更加精确,即逼近于DTFT的波形,有两种方法。第一种方法是採样长度和DFT长度都添加,假设可能应该尽可能採取这样的方法,这样的方法能提高实际的分辨率,降低泄漏。另外一种方法是添加DFT长度,而採样长度通过补零补到一样的长度。这样的方法仅仅能添加视在分辨率。该泄漏的还是泄漏了。