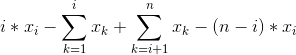曼哈顿距离与切比雪夫距离(知识点总结+例题整理)

思路来源

https://www.cnblogs.com/zwfymqz/p/8253530.html

心得

其实就是旋转坐标系，先旋转再伸缩

一般曼哈顿距离直接做不好做的，可以转成切比雪夫距离试试看

结论

将一个点(x,y)的坐标变为后，原坐标系中的曼哈顿距离=新坐标系中的切比雪夫距离

将一个点(x,y)的坐标变为 后，原坐标系中的切比雪夫距离=新坐标系中的曼哈顿距离

第二个显然是第一个的逆变换，所以记第一个就好

例题

①洛谷P3964 [TJOI2013]松鼠聚会

https://www.luogu.com.cn/problem/P3964 松鼠聚会

N<=1e5个点，点i坐标(xi,yi)(-1e9<=xi,yi<=1e9)，

求N个点中的一点使得其余点到这一点切比雪夫距离和最小，输出距离和

先转曼哈顿距离，计i,j曼哈顿距离为，将x和y分开考虑

将x按增序排列，最后肯定是求

等价于，排序之后前缀和枚举二分搞一搞

具体实现时，先按((x+y)/2,(x-y)/2)转曼哈顿坐标，确保整数坐标*2，最后将距离/2即可

#include
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll sx[N],sy[N],ans,tmp;
int n,x[N],y[N],idx,idy;
struct node
{
	int x,y;
}e[N];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	{
		scanf("%d%d",&e[i].x,&e[i].y);
		x[i]=e[i].x+e[i].y,y[i]=e[i].x-e[i].y;
		e[i].x=x[i],e[i].y=y[i];
	}
	sort(x+1,x+n+1);
	sort(y+1,y+n+1);
	for(int i=1;i<=n;++i)
	{
		sx[i]=sx[i-1]+x[i];
		sy[i]=sy[i-1]+y[i];
	}
	ans=8e18; 
	for(int i=1;i<=n;++i)
	{
		idx=lower_bound(x+1,x+n+1,e[i].x)-x;
		idy=lower_bound(y+1,y+n+1,e[i].y)-y;
		tmp=1ll*idx*e[i].x-sx[idx]+(sx[n]-sx[idx])-1ll*(n-idx)*e[i].x;
		tmp+=1ll*idy*e[i].y-sy[idy]+(sy[n]-sy[idy])-1ll*(n-idy)*e[i].y;
		ans=min(ans,tmp);
	}
	printf("%lld\n",ans/2);
	return 0;
}

②牛客挑战赛34

https://ac.nowcoder.com/acm/contest/2271/D 拉普兰德的愿望

n(n<=1e5)个点，点的范围(x,y)的绝对值在L(L<=5e4)内，

求有多少点对的曼哈顿距离不小于d(d<=1e7)

 

用总的点对减去小于d的点对，把曼哈顿距离转化为切比雪夫距离

等价于判切比雪夫距离为d的正方形以内(不含矩形轮廓线)的点对有多少个

考虑到用每个正方形的左半部分去取点，这样每个点对只会记录一次，(左,右)

二维偏序问题，x排增序，按y值插入到BIT上，询问[y-d+1,y+d-1]的和，

x的距离每超过d时，就从BIT里把之前插的点删去

#include
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,d,l,a,b,tr[N*2];
ll ans;
struct node
{
	int x,y;
}e[N];
bool operator<(node a,node b)
{
	return a.x0;i-=i&-i)
	ans+=tr[i];
	return ans;
}
int main()
{
	scanf("%d%d%d",&n,&d,&l);
	for(int i=1;i<=n;++i)
	{
		scanf("%d%d",&a,&b);
		e[i].x=a+b+2*l;
		e[i].y=a-b+2*l; 
	}
	sort(e+1,e+n+1);
	ans=1ll*n*(n-1)/2;
	for(int i=1,now=1;i<=n;++i)
	{
		while(now=d)
		{
			add(e[now].y,-1);
			now++;
		}
		ans=(ans-(sum(min(4*l,e[i].y+d-1))-sum(max(0,e[i].y-d))));//[y-d+1,y+d-1]
		add(e[i].y,1); 
	}
	printf("%lld\n",ans); 
	return 0;
}

③四川大学第二届SCUACM新生赛（同步赛）

https://ac.nowcoder.com/acm/contest/1838/H 捡金币

T(T<=100)组样例，每次给出n*m(n,m<=1e3)的棋盘，每个格子放入的金币数v(1<=v<=1e6)，

q(q<=1e5)组询问，每次给出(x,y)和距离k，询问到(x,y)曼哈顿距离小于等于k的金币数之和

 

其实感觉T=100时时间1s有点极限，先转切比雪夫距离到2e3*2e3的数组，

二维前缀和预处理，对于询问O(1)回答即可

#include
using namespace std;
typedef long long ll;
const int N=2010;
int t,n,m,q,mp[N][N];
int a,c,b,d,x,y,k,v;
ll sum[N][N];
ll cal(int a,int c,int b,int d)
{
	return sum[b][d]-sum[a-1][d]-sum[b][c-1]+sum[a-1][c-1];
}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d",&n,&m);
		for(int i=0;i<=n+m;++i)
		{
			for(int j=0;j<=n+m;++j)
			mp[i][j]=sum[i][j]=0;
		}
		for(int i=1;i<=n;++i)
		{
			for(int j=1;j<=m;++j)
			{
				scanf("%d",&v);
				x=i+j;y=i-j+m;
				mp[x][y]+=v;
			}
		}
		for(int i=1;i<=n+m;++i)
		{
			for(int j=1;j<=n+m;++j)
			{
				sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+mp[i][j];
			}
		}
		for(scanf("%d",&q);q;q--)
		{
			scanf("%d%d%d",&a,&b,&k);
			x=a+b;y=a-b+m;
			a=max(1,x-k),c=max(1,y-k);
			b=min(n+m,x+k),d=min(n+m,y+k);
			printf("%lld\n",cal(a,c,b,d));
		}
	}
	return 0;
}
/*
3 4
1 2 3 4
5 6 7 8
9 10 11 12
4
2 2 0
2 2 1
2 2 2
2 2 3
*/

④统计曼哈顿距离内扫描线可以转成矩形的扫描线

https://blog.csdn.net/Code92007/article/details/98517541