CORDIC算法详解(二)-CORDIC 算法之圆周系统之向量模式

CORDIC算法详解（二）- CORDIC 算法之圆周系统之向量模式（Vectoring Mode）

  网上有很多类似的介绍，但是本文会结合实例进行介绍，尽量以最简单的语言进行解析。
  CORDIC ( Coordinate Rotation Digital Computer ) 是坐标旋转数字计算机算法的简称，
由 Vloder• 于 1959 年在设计美国航空导航控制系统的过程中首先提出[1], 主要用于解决导航系统中三角函数、 反三角函数和开方等运算的实时计算问题。 1971 年， Walther 将圆周系统、 线性系统和双曲系统统一到一个 CORDIC 迭代方程里 ， 从而提出了一种统一的CORDIC 算法形式[2]。
  CORDIC 算法应用广泛， 如离散傅里叶变换 、 离散余弦变换、 离散 Hartley 变换、Chirp-Z 变换、 各种滤波以及矩阵的奇异值分解中都可应用 CORDIC 算法。 从广义上讲，CORDIC 算法提供了一种数学计算的逼近方法。 由于它最终可分解为一系列的加减和移位操作， 故非常适合硬件实现。 例如， 在工程领域可采用 CORDIC 算法实现直接数字频率合成器。 本节在阐述 CORDIC 算法三种旋转模式的基础上， 介绍了利用 CORDIC 算法计算三角函数、 反三角函数和复数求模等相关理论。 以此为依据， 阐述了基于 FPGA 的 CORDIC 算法的设计与实现及其工程应用。

---

整个系列分别从圆周系统、 线性系统和双曲系统及硬件实现进行分析，如下：

CORDIC算法详解（一）- CORDIC 算法之圆周系统之旋转模式（ Rotation Mode )
CORDIC算法详解（二）- CORDIC 算法之圆周系统之向量模式（Vectoring Mode）
CORDIC算法详解（三）- CORDIC 算法之线性系统及其数学应用
CORDIC算法详解（四）- CORDIC 算法之双曲系统及其数学应用
CORDIC算法详解（五）- 统一的 CORDIC 算法形式
CORDIC算法详解（六）- CORDIC 算法的硬件实现
其中第五篇及第六篇后会放出相关参考资料及源码。

---

2 CORDIC 算法之圆周系统之向量模式（Vectoring Mode）

2.1 向量模式（Vectoring Mode）

  在向量模式下， CORDIC 算法主要用于实现直角坐标系到极坐标系的转换 旋转模式下， 每次迭代使 z 趋向于 0。与之相比， 向量模式下， 则是使y趋向于 0。 为了达到这一目标， 每次迭代通过判断 y_i 的符号确定旋转方向， 最终使初始向量旋转至 X 轴的正半轴， 这一过程也使得每次微旋转的旋转角度累加和存储在变量 z 中。 矢量旋转图如图 3.76 所示， 相应的迭代过程如式（3.110) 所示：

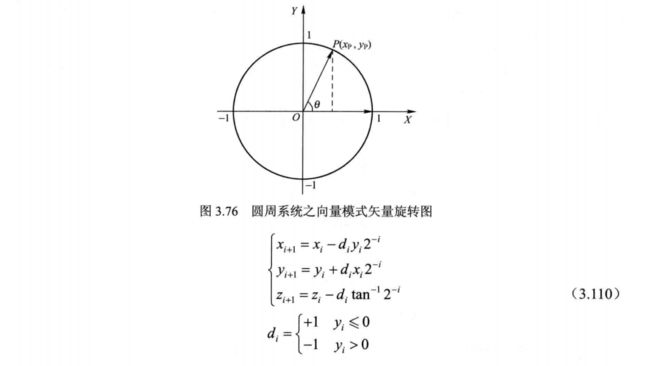
  经过n(n–>∞)次旋转，使图3.76中的P靠近x轴。因此，当迭代结束之后，P将近似接近x轴，此时P点纵坐标y_n = 0，在这个过程中可知旋转了θ，即z_n = z₀ +θ = z₀+arctan(y₀/x₀)(z₀为初始化角度)。
  由上一篇文章可知，每次微旋转都导致向量模长发生了变化。以K_i表示第 i次微旋转模长补偿因子， 故第 i次微旋转真实旋转的结果应为:

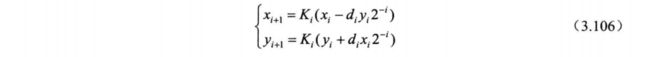
  其中，由于在伪旋转中，去掉了cosθ_i，所以K_i=cosθ_i 由式 (3.99) 可知:

  当n趋于无穷大时，K 逼近 0.607252935。
  经过n(n–>∞)次旋转，可得：

• x_n = 1/∏cosθ_i(x₀cosθ – y₀sinθ)（其中i从0至n-1）
• y_n = 1/∏cosθ_i(y₀cosθ + x₀sinθ)（其中i从0至n-1）

  因此，可得y₀cosθ + x₀sinθ = 0，

• x_n = 1/∏cosθ_i(x₀cosθ – y₀sinθ) = 1/∏cosθ_i{ [ (x₀cosθ – y₀sinθ)²]^(1/2)}(平方再开方)
  = 1/∏cosθ_i{ [ x₀²cos²θ + y₀²sin²θ – 2x₀y₀sinθcosθ]^(1/2)}
  = 1/∏cosθ_i{ [ x₀²cos²θ + y₀²sin²θ + y₀²cos²θ + x₀²sin²θ ]^(1/2)}
  = 1/∏cosθ_i{ [ x₀² + y₀²]^(1/2)}

   得到的最终结果为

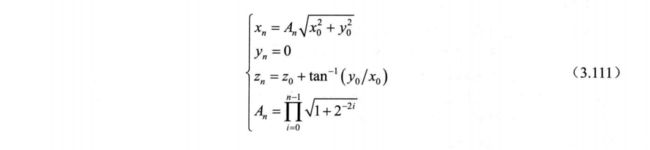
  式( 3.111 ) 中， 要求初始化角度 z₀ = 0 , 从而可获得向量的模长和相角。 以向量(1，2)为例，其旋转过程如表 3.20 所示， 前 3 次微旋转矢量图如图 3.77 所示。


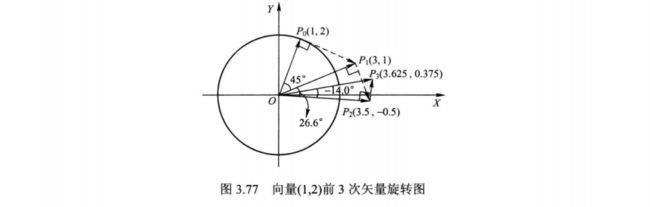
  旋转模式和向量模式的相同之处在于： 两者都是微旋转， 也都是伪旋转。 前者使得向量模式下的初始向量必须落入第一或第四象限； 后者使得向量模长发生变化需要补偿。

2.2 思考

  若初始向量落入第二或第三象限该如何处理？
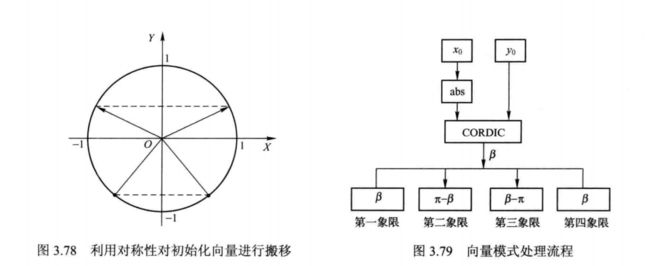
  由于微旋转限定了初始向量必须在第一或第四象限 ，这就要求 x₀ > 0 ，而对 y₀没有要求。根据对称性，当初始向量位于第二象限时，将其搬移至第一象限；当初始向量位于第三象限时，将其搬移至第四象限，如图3.78所示，然后在对搬移后的向量利用CORDIC算法进行处理。对CORDIC处理的结果，根据 x₀ 和 y₀的符号（判断初始向量所在的象限）做对应的处理，从而获得初始向量的相角，处理流程如图如图 3.79 所示。

2.3 CORDIC 算法之圆周系统之向量模式应用

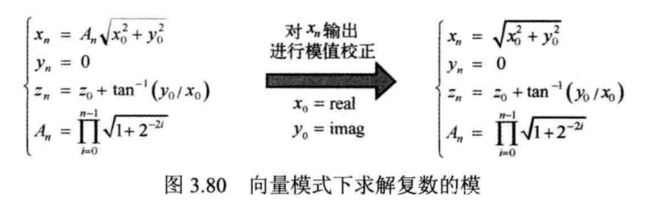
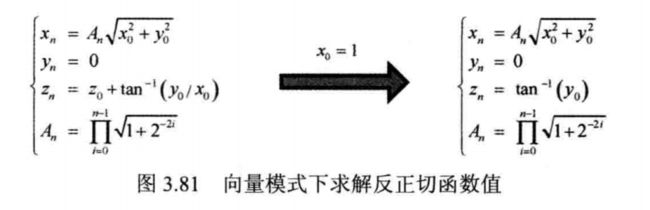
  根据式 （3.111 ), 取x₀ 为复数的实部， y₀为复数的虚部， 利用 CORDIC 算法可以进行复数求模运算， 显然， 也可求出该复数的相位， 如图 3.80 所示。 这里并不要求(x₀ ， y₀ )在单位圆上。

  同样地， 根据式（ 3.111 ), 令x ₀ = 1 , 可获取反正切函数值， 如图 3.81 所示。 据此， 在   MATLAB 下求解反正切函数值如图 3.82 所示。   关于CORDIC算法计算反三角函数arctanθ的MATLAB代码如下所示：

close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 100;%初始设置
y(1) = 200;%初始设置
k = 0.607253;%初始设置
%迭代操作
for i = 1:die
    if y(i) >= 0
        d = -1;
    else
        d = 1;
    end
    x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));
    y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));
    z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
d = vpa(x(17)*k,10)
a = vpa(y(17),10)
c = vpa(rad2deg(z(17)),10)

  此外，根据式（3.111），还可以实现直角坐标系到极坐标的转换。最终x _n输出为极径，但扩大为初始向量模长的A _n，对z _n进行一定的处理后即为极角。

3 CORDIC 算法之圆周系统之向量模式及圆周模式应用

  CORDIC圆角系统算法模型如MATLAB代码如下。其中，cordic_cr调用了两个函数cordic_cr_pre和cordic_cr_post，分别如MATLAB代码3-4和MATLAB代码3-5所示。

MATLAB代码3-3 function : cordic_cr

% /*
% * @Author: ZLK
% * @Date:   2018-10-30 16:30:29
% * @Last Modified by:   ZLK
% * @Last Modified time: 2018-10-30 17:13:55
% */
function a = cordic_cr(x0,y0,z0,mode,it)
% Circular Rotation.
% mode 0: roatation mode; 1: vectoring mode.
% vectoring mode: z0=0.
% z0: expected rotation angle with rad instead of degree.
% In rotation mode z0 ranges from -pi to pi.
% it: iteration count
%% cordic_cr_pre
[x0_p,y0_p,z0_p]=cordic_cr_pre(x0,y0,z0,mode);
x = zeros(it+1,1);
y = zeros(it+1,1);
z = zeros(it+1,1);
x(1)= x0_p;
y(1)= y0_p;
z(1)= z0_p;
di = 0;
%% iteration
for k=1:it
	if mode==0
		di = sign(z(k)); % rotation mode
	else
		di = sign(-y(k));% vectoring mode
	end
	x(k+1) = x(k)-y(k)*di*2^(-(k-1));
	y(k+1) = y(k)+x(k)*di*2^(-(k-1));
	z(k+1) = z(k)-di*atan(2^(-(k-1)));
end
kn = 1/prod(sqrt(1+2.^(-2*(0:it-1)))); % scale factor
xn_p = kn*x(it+1);
yn_p = kn*y(it+1);
zn_p = z(it+1);
%% cordic_cr_ post
[xn,yn,zn]=cordic_cr_post(x0,y0,z0,xn_p,yn_p,zn_p,mode);
%% true result
if mode==0
	xt = x0*cos(z0)-y0*sin(z0);
	yt = y0*cos(z0)+x0*sin(z0);
	zt = 0;
else
	xt = sqrt(x0^2+y0^2);
	yt = 0;
	zt = z0+atan2(y0,x0); % atan2 rang from -pi to pi
end
a = [xn,xt,yn,yt,zn,zt];

MATLAB代码3-4 function : cordic_cr_pre

% /*
% * @Author: ZLK
% * @Date:   2018-10-30 16:30:29
% * @Last Modified by:   ZLK
% * @Last Modified time: 2018-10-30 16:44:24
% */
function [x0_p,y0_p,z0_p]=cordic_cr_pre(x0,y0,z0,mode)
% vector (x0,y0)
% mode : 0 : rotation; else vectoring
if z0<-pi||z0>pi
	error('Rotation angle must range from -pi to pi.');
end

if x0==0 && y0==0
	error('Both x0 and y0 can not be zeros at the same time.');
end

if mode==0
	s = sign(z0);
	if z0>pi/2||z0<-pi/2
	x0_p= -s*y0;
	y0_p = s*x0;
	z0_p = z0 - s*pi/2;
else
	x0_p = x0;
	y0_p = y0;
	z0_p = z0;
end
else
	x0_p = abs(x0);
	y0_p = abs(y0);
	z0_p = 0;
end

MATLAB代码3-5 cordic_cr_post

% /*
% * @Author: ZLK
% * @Date:   2018-10-30 16:30:42
% * @Last Modified by:   ZLK
% * @Last Modified time: 2018-10-30 16:55:58
% */
function [xn,yn,zn]=cordic_cp_post(x0,y0,z0,xnp,ynp,znp,mode)
% mode : 0 : rotation; else vectoring
theta = 0;
if mode==1
	if x0>=0 && y0>=0
		theta = znp;
	elseif x0<0 && y0>=0
		theta = pi - znp;
	elseif x0<0 && y0<=0
		theta = znp - pi;
	elseif x0>0 && y0<0
		theta = -znp;
	end
		xn = xnp;
		yn = ynp;
		zn = z0 + theta;
else
	xn=xnp;
	yn = ynp;
	zn = znp;
end

验证

  在命令行输入：cordic_cr(0.607253,0,pi/4,0,16)
  上诉命令为计算cosθ和sinθ，其中θ=π/4（迭代次数16）
  结果：

• x₁₇=0.707095876358217
• y₁₇=0.707117836980767