电压校准
实验数据与曲线拟合算法实现
实际电压与采样电压
比较采样电压与实际电压存在误差的关系,根据关系设计纠正算法。
曲线拟合
最小二乘法曲线拟合
使用最小二乘法拟合是曲线拟合的一种常用方法。
选取合适的匹配模式是该方法的关键,如果离散数据呈现的是指数变化规律,则应该选择指数形式的匹配函数模式,如果是多项式变化规律,则应该选择多项式匹配模式,如果选择的模式不对,拟合的效果就会很差,这也是使用最小二乘法进行曲线拟合时需要特别注意的一个地方。
具体做法
电压采样
利用多个单片机对同一组输入电压进行测量和记录
实际电压
vol[] = [3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, ...
11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0, 19.0, 20.0,...
21.0, 22.0, 23.0, 24.0, 25.0, 26.0, 27.0, 28.0, 29.0, 30.0,];
得到三组采样数据
采样电压
vol1[] = [2.93, 3.92, 4.91, 5.88, 6.86, 7.84, 8.81, 9.79, ...
10.77, 11.75, 12.73, 13.70, 14.68, 15.67, 16.65, 17.63, 18.61, 19.58,...
20.56, 21.54, 22.52, 23.49, 24.47, 25.46, 26.43, 27.42, 28.40, 29.38,];
vol2[] = [2.91, 3.87, 4.84, 5.81, 6.78, 7.74, 8.71, 9.67, ...
10.65, 11.62, 12.58, 13.54, 14.51, 15.48, 16.46, 17.43, 18.39, 19.36,...
20.32, 21.30, 22.26, 23.22, 24.20, 25.16, 26.13, 27.11, 28.06, 29.04,];
vol3[] = [2.90, 3.86, 4.84, 5.81, 6.77, 7.74, 8.70, 9.67, ...
10.65, 11.62, 12.60, 13.56, 14.53, 15.50, 16.47, 17.44, 18.40, 19.37,...
20.34, 21.31, 22.28, 23.25, 24.21, 25.19, 26.16, 27.13, 28.09, 29.07,];
matlab散点拟合曲线
函数y = f(x), y为实际电压,x为采样电压。利用matlab对实际电压和采样电压进行曲线离合,得到y = f(x)的合适的方程式。
步骤
1、在工作空间中存入变量的实验数据。具体如下:
可以直接用矩阵来存放数据,直接在命令窗口输入
x=[数据x1,数据x2,…,数据xn];
y=[数据y1,数据y2,…,数据yn];
当数据较多时,可以从excel,txt等文件中导入。
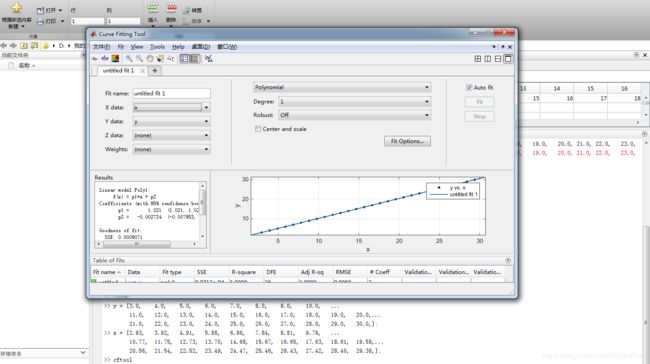
2、把数据存入工作空间后,在命令窗口中输入cftool,回车运行
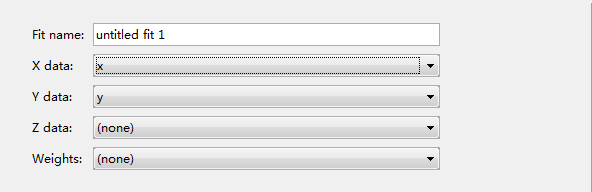
3、在这个拟合工具窗口的左边,选择变量,即分别选择x,y。
4、选择拟合的曲线类型
选择完后会自动完成拟合,并且给出拟合函数表达式。可以看出这个曲线的拟合度非常好,所以可以得出方程式为 y = p1* x + p2; p1 = 1.021, p2 = -0.002734。如果曲线拟合度不好,可以继续更改曲线或者Degree;
-
Results :显示当前拟合的详细结果, 包括拟合类型 (模型、样条或插值函数)、拟合系数以及参数匹配的95% 置信范围, 以及适合统计的这些优点;
-
SSE: 错误的平方和。此统计量测量响应的拟合值的偏差。接近0的值表示更好的匹配。
-
R-square 表示:多重测定系数。数值的大小在0到1之间,越接近1,表明方程的变量对y的解释能力越强。
-
Adjusted R-square:自由度调整 r 平方。接近1的值表示更好的匹配。当您向模型中添加附加系数时, 它通常是适合质量的最佳指示器。
-
RMSE:均方根误差。接近0的值表示更好的匹配。
5、依次对三组数据进行曲线拟合。