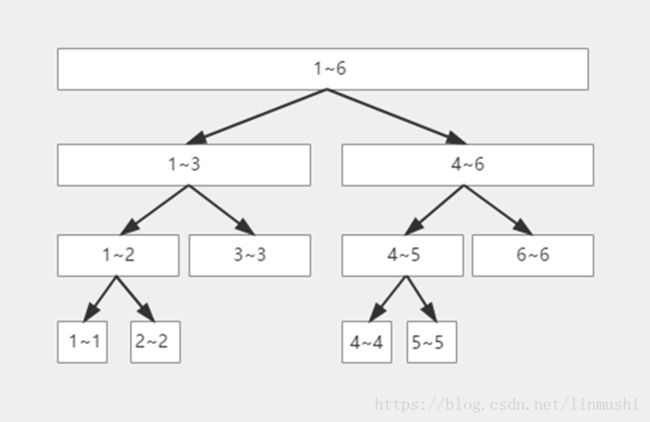
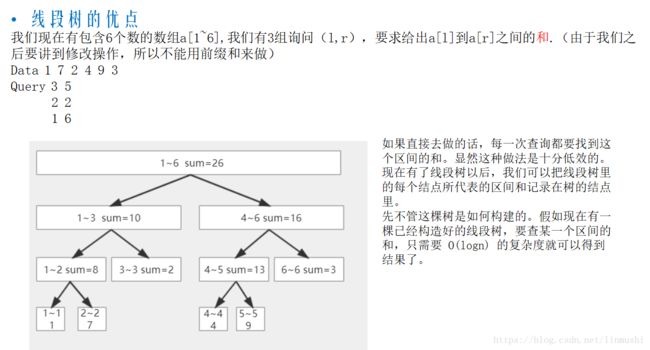
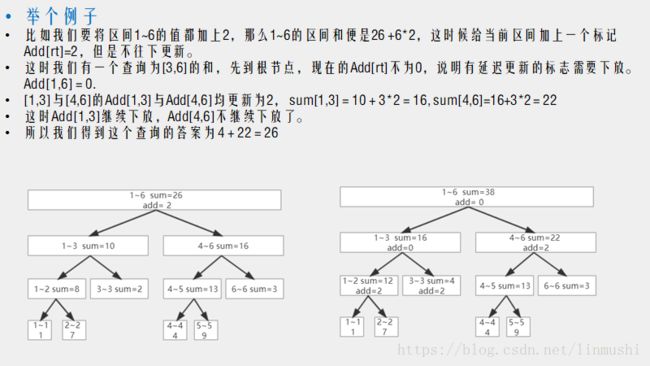
线段树 学习 模板 单点更新 区间更新

线段树是干什么的？有一列数，每次可以进行以下三种操作中的一种：（1） 给指定区间中的每个数都加上某个值；（2） 将指定区间内的所有数置成某一个统一的值；（3） 询问一个区间上的最小值、最大值、所有数的和。朴素做法怎么做？用线性表存储，每种操作，对待处理或待询问区间中的每个元素都逐一进行处理。复杂度多少？假设这个数列的长度为n，总的操作数为m，则这个算法每次维护的时间复杂度为O(n)，整体的时间复杂度为O(mn)为什么慢？所有的维护都是针对元素的，而题目中所有的维护要求却都是针对区间的。

、

#include 
 #define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
const int maxn = 55555;
int sum[maxn<<2];
void PushUP(int rt) {
       sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void build(int l,int r,int rt) {
       if (l == r) {
              scanf("%d",&sum[rt]);
              return ;
       }
       int m = (l + r) >> 1;
       build(lson);
       build(rson);
       PushUP(rt);
}
void update(int p,int add,int l,int r,int rt) {
       if (l == r) {
              sum[rt] += add;
              return ;
       }
       int m = (l + r) >> 1;
       if (p <= m) update(p , add , lson);
       else update(p , add , rson);
       PushUP(rt);
}
int query(int L,int R,int l,int r,int rt) {
       if (L <= l && r <= R) {
              return sum[rt];
       }
       int m = (l + r) >> 1;
       int ret = 0;
       if (L <= m) ret += query(L , R , lson);
       if (R > m) ret += query(L , R , rson);
       return ret;
}
int main() {
       int T , n;
       scanf("%d",&T);
       for (int cas = 1 ; cas <= T ; cas ++) {
              printf("Case %d:\n",cas);
              scanf("%d",&n);
              build(1 , n , 1);
              char op[10];
              while (scanf("%s",op)) {
                     if (op[0] == 'E') break;
                     int a , b;
                     scanf("%d%d",&a,&b);
                     if (op[0] == 'Q') printf("%d\n",query(a , b , 1 , n , 1));
                     else if (op[0] == 'S') update(a , -b , 1 , n , 1);
                     else update(a , b , 1 , n , 1);
              }
       }
       return 0;
}

#include 
 #define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
const int maxn = 100050;
typedef long long ll;
ll sum[maxn<<2];
ll Add[maxn<<2]; 
void PushUP(int rt) {
       sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void PushDown(int rt,int ln,int rn){  
    //ln,rn为左子树，右子树的数字数量。   
    if(Add[rt]){  
        //下推标记   
        Add[rt<<1]+=Add[rt];  
        Add[rt<<1|1]+=Add[rt];  
        //修改子节点的Sum使之与对应的Add相对应   
        sum[rt<<1]+=Add[rt]*ln;  
        sum[rt<<1|1]+=Add[rt]*rn;  
        //清除本节点标记   
        Add[rt]=0;  
    }  
} 
void build(int l,int r,int rt) {
       if (l == r) {
              scanf("%d",&sum[rt]);
              return ;
       }
       int m = (l + r) >> 1;
       build(lson);
       build(rson);
       PushUP(rt);
}
void Update(int L,int R,int C,int l,int r,int rt){
    //L,R表示操作区间l,r表示当前节点区间，rt表示当前节点编号   
    if(L <= l && r <= R){//如果本区间完全在操作区间[L,R]以内   
        sum[rt]+=C*(r-l+1);//更新数字和，向上保持正确  
        Add[rt]+=C;//增加Add标记，表示本区间的Sum正确，子区间的Sum仍需要根据Add的值来调整  
        return ;   
    }  
    int m=(l+r)>>1;  
    PushDown(rt,m-l+1,r-m);//下推标记  
    //这里判断左右子树跟[L,R]有无交集，有交集才递归   
    if(L <= m) Update(L,R,C,l,m,rt<<1);  
    if(R >  m) Update(L,R,C,m+1,r,rt<<1|1);   
    PushUP(rt);//更新本节点信息   
}

ll Query(int L,int R,int l,int r,int rt){//L,R表示操作区间，l,r表示当前节点区间，rt表示当前节点编号  
    if(L <= l && r <= R){  
        //在区间内，直接返回   
        return sum[rt];  
    }  
    int m=(l+r)>>1;  
    //下推标记，否则Sum可能不正确  
    PushDown(rt,m-l+1,r-m);   
    //累计答案  
    ll ANS=0;  
    if(L <= m) ANS+=Query(L,R,l,m,rt<<1);  
    if(R >  m) ANS+=Query(L,R,m+1,r,rt<<1|1);  
    return ANS;  
} 

int main() {
	int n, m;
	scanf("%d%d",&n, &m);
 	build(1 , n , 1);
    while (m--) {
 		int q, x, y, k;
  		scanf("%d", &q);
   		if (q == 1){
		   	scanf("%d%d%d", &x, &y, &k);
		   	Update(x, y, k, 1, n, 1);
	    }
		else{
			scanf("%d%d", &x, &y);
			printf("%lld\n",Query(x, y, 1, n, 1));
		}
    }
    return 0;
}