- 带标签的 Docker 镜像打包为 tar 文件
大霸王龙
docker容器运维
现在还有人用docker吗要将带标签的Docker镜像打包为tar文件,请使用dockersave命令。以下是详细操作指南:一、单镜像打包(推荐方式)#基础格式dockersave-o[输出文件名].tar[镜像名]:[标签]#示例:将my-app:1.0保存为app-backup.tardockersave-oapp-backup.tarmy-app:1.0二、多镜像打包#同时打包多个镜像到单个
- 从零开始理解零样本学习:AI人工智能必学技术
AI天才研究院
AgenticAI实战AI人工智能与大数据AI大模型企业级应用开发实战ai
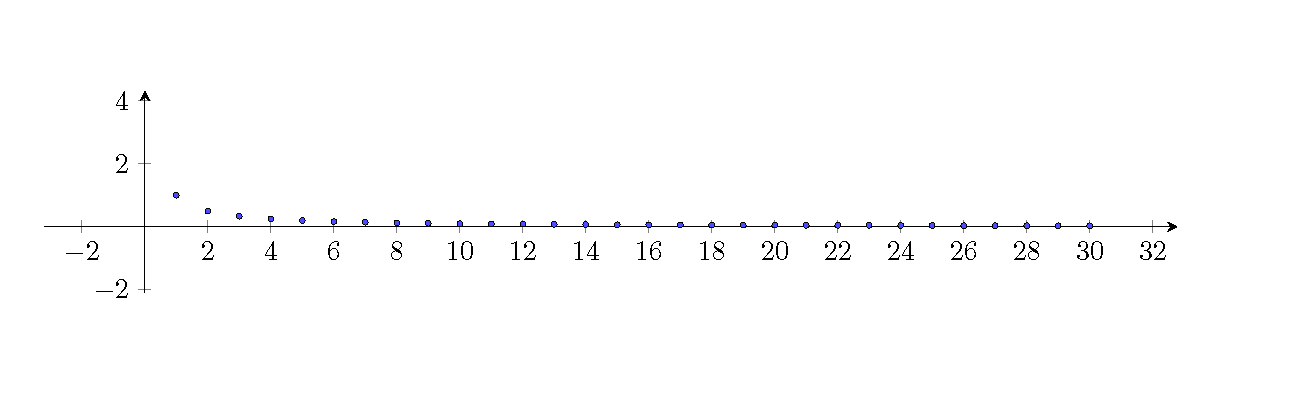
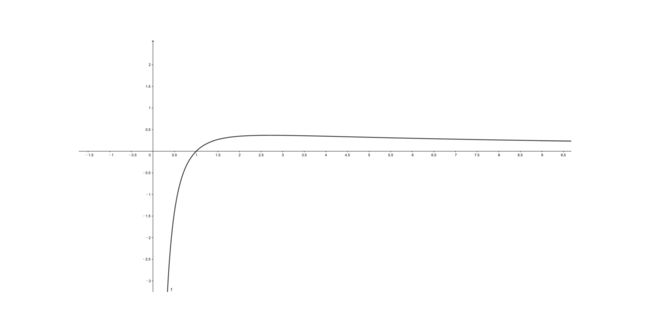
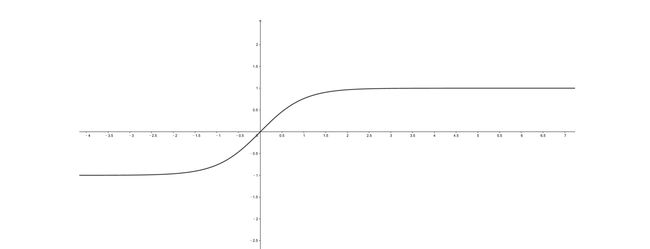
从零开始理解零样本学习:AI人工智能必学技术关键词:零样本学习、人工智能、机器学习、知识迁移、语义嵌入摘要:本文旨在全面深入地介绍零样本学习这一在人工智能领域具有重要意义的技术。首先阐述零样本学习的背景和基本概念,通过详细的解释和直观的示意图让读者建立起对零样本学习的初步认识。接着深入剖析其核心算法原理,结合Python代码进行详细说明,同时引入相关数学模型和公式并举例阐释。通过项目实战部分,带领
- 常见的会话劫持攻击是指什么?
wanhengidc
安全网络web安全
会话劫持攻击是一种常见的网络安全攻击,恶意攻击者通过窃取用户的会话标识符号来接管用户的会话,当攻击者或者有效的会话标识符,那么就可以借取正常用户的数据信息,来访问目标用户的账号,并进行各种操作,来修改或者盗取重要的数据信息,以此来给用户造成巨大的经济损失。所以企业对于会话劫持攻击,可以选择定期更新和修补系统漏洞来保护用户的数据安全,及时更新操作系统、应用程序和安全组件,以此来修复已知的服务器安全漏
- Java中的批处理优化:使用Spring Batch处理大规模数据的实践
微赚淘客系统开发者@聚娃科技
javaspringbatch
Java中的批处理优化:使用SpringBatch处理大规模数据的实践大家好,我是微赚淘客返利系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!在处理大规模数据的场景中,批处理是一个非常常见且必要的操作。Java中的SpringBatch是一个强大的框架,能够帮助我们高效地执行复杂的批处理任务。本文将带大家了解如何使用SpringBatch处理大规模数据,并通过代码示例展示如何实现高效的批
- 稳定币独角兽:Circle
InnoLink_1024
区块链稳定币区块链
Circle公司背景分析CircleInternetFinancial(以下简称Circle)是一家成立于2013年的美国金融科技公司,总部位于波士顿,由JeremyAllaire和SeanNeville联合创立。公司最初专注于点对点加密货币支付和交易,后转型为全球领先的稳定币发行机构,其核心产品是与美元1:1挂钩的USDCoin(USDC),目前为全球第二大稳定币,仅次于Tether的USDT。
- Cline中配置MCP
Alexon Xu
MCP
1、自动安装MCP默认AI生成的配置会报错:spawnnpxENOENTspawnnpxENOENT,然后排查了npx安装都是OK的,需要使用cmd运行npx,配置如下:{"mcpServers":{"sequentialthinking":{"autoApprove":[],"disabled":false,"timeout":60,"command":"cmd.exe","args":["/c
- deepseek: 通过命令行将 Windows 11 的右键菜单改为 Windows 10 风格
Alexon Xu
deepseekwindows
要通过命令行将Windows11的右键菜单改为Windows10风格,可以使用reg命令直接修改注册表。以下是具体步骤:使用命令行修改注册表打开命令提示符(以管理员身份运行),然后执行以下命令:启用Windows10风格的右键菜单regadd"HKCU\Software\Classes\CLSID\{86ca1aa0-34aa-4e8b-a509-50c905bae2a2}\InprocServe
- js递归性能优化
啃火龙果的兔子
开发DEMOjavascript开发语言ecmascript
JavaScript递归性能优化递归是编程中强大的技术,但在JavaScript中如果不注意优化可能会导致性能问题甚至栈溢出。以下是几种优化递归性能的方法:1.尾调用优化(TailCallOptimization,TCO)ES6引入了尾调用优化,但只在严格模式下有效:'usestrict';//普通递归functionfactorial(n){if(n===1)return1;returnn*fa
- 2025 VUE常见面试题
hmildj
vue.js面试前端
前言总结一些VUE面试的基础知识,共同学习1.什么是Vue?答案:Vue.js(通常简称为Vue)是一个用于构建用户界面的渐进式JavaScript框架,Vue3是Vue.js框架的最新版本,它引入了许多改进和优化,包括性能提升、更好的类型支持、组合API等。2.MVVM模式是什么?Vue如何体现这一模式?答案:MVVM将视图(View)与数据(Model)通过ViewModel层解耦,Vue
- 软件测试从业者必备的SQL知识
十二测试录
数据库sql数据库
作为职场人,学一门技能是用来解决日常工作问题的,没必要从头到尾把这块知识弄透,没那么多时间。基于此,十二根据自己的经验,把软件测试从业者需要掌握的SQL知识,整理如下;只要跟着这个顺序,从头到尾执行即可。前置准备事项:1、在自己电脑上安装一个mysql数据库,文章见->虚拟机Centos下安装Mysql完整过程(图文详解)_虚拟机安装mysql-CSDN博客2、找一个mysql客户端链接工具:初学
- Script to save all images from a docker-compose.yml file
唧唧歪歪的
dockerdockerdocker-compose
通过docker-compose.yml导出镜像到单个文件Scripttosaveallimagesfromadocker-compose.ymlfile1st#!/bin/bashmkdir-poutforimgin`grepimage$1|sed-e's/^.*image\://g'`;docleanname=${img/\//-}tag=`dockerimages|grep$img|awk'
- RPC:跨越代码与硅晶的“握手”——你每天都在用,却可能从未真正理解它
老马爱知
信息技术#分布式计算rpc网络协议网络分布式系统微服务软件架构硬核科普
——从本地调用的幻觉到服务万物的底座,解析这个支配云原生时代的隐形协议引言:一个程序员的日常困境想象一下这个场景:你正在构建一个电商系统。用户服务(管理用户信息)在一台服务器上,订单服务在另一台,而支付服务,则由远在天边的第三方提供。当一个用户下单时,订单服务需要先向用户服务确认用户身份,再调用支付服务完成扣款。这三个服务如同三座孤岛,如何让它们高效、优雅地对话?难道你要手动编写Socket连接,
- Java静态static详解
Obltv
Java基础java
更多内容请看我的个人网站date:2025-06-04tags:八股基础静态变量特点被该类的所有对象共享不属于对象,属于类优先于对象存在,随着类的加载而加载调用方式类名调用对象名调用(不推荐)静态方法没有this关键字publicclassStudent{privateStringname;privateintage;privateStringteacherName;publicvoidshow(
- Java中多态的一些见解
更多内容请看我的个人网站多态初识调用成员的特点成员变量:编译看左边,运行看左边成员方法:编译看左边,运行看右边多态在调用成员变量时为什么是父类的,但是方法是子类的?一句话解释:在编译时(静态绑定),成员变量是根据引用类型(也就是声明的类型)来决定的;在运行时(动态绑定),方法是根据对象的实际类型(也就是new出来的类型)来决定的。举个经典例子classParent{publicStringname
- Java中的值传递
Obltv
Java基础java开发语言
更多内容请看我的个人网站date:2025-06-01tags:八股基础Java中只有值传递什么是值传递值传递(PassbyValue)调用方法时,传递的是参数的值,是原始数据的一个副本。方法内部改变这个副本,不影响原始数据。什么是引用传递引用传递(PassbyReference)调用方法时,传递的是变量的地址(指针),方法内部对这个引用的任何更改,都会影响原始对象的引用。举例一个方法不能修改一个
- 初学翁凯老师的c语言后对其中一些问题的看法
Obltv
#初学c语言c语言
文章目录初学翁凯老师的c语言后对其中一些问题的看法一、一个课后的简单逻辑语法问题二、解答和一些思考1.**++i++--**2.**i++++**3.**a=b+=c++-d+--e/-f**问题初探原代码逻辑举例初次写博客的看法及感受初学翁凯老师的c语言后对其中一些问题的看法学习c语言已有数天,其中一些问题今日来看仍有研究价值,故记录探讨之一、一个课后的简单逻辑语法问题++i+±-i++++a=
- Vue 3 的 <script setup> 语法糖与 TypeScript 的深度整合
前端熊猫
vue.jstypescriptscript前端
在Vue单文件组件中,标签除了lang、async、defer、src和name属性外,还有一些其他重要属性和用法值得关注。以下是补充说明及优化建议:一、setup属性(CompositionAPI核心)作用:通过setup属性启用Vue3的CompositionAPI,简化逻辑组织和复用。代码示例:import{ref,onMounted}from'vue'constcount=ref(0)on
- 高斯混合模型(Gaussian Mixture Model, GMM)
不想秃头的程序
神经网络语音识别人工智能深度学习网络
高斯混合模型(GaussianMixtureModel,GMM)是一种概率模型,用于表示数据点由多个高斯分布(GaussianDistribution)混合生成的过程。它广泛应用于聚类分析、密度估计、图像分割、语音识别等领域,尤其适合处理非球形簇或多模态数据。以下是GMM的详细介绍:一、核心思想GMM假设数据是由多个高斯分布混合生成的,每个高斯分布代表一个簇(Cluster),并引入隐变量(Lat
- 卷积神经网络(Convolutional Neural Network, CNN)
不想秃头的程序
神经网络语音识别人工智能深度学习网络卷积神经网络
卷积神经网络(ConvolutionalNeuralNetwork,CNN)是一种专门用于处理图像、视频等网格数据的深度学习模型。它通过卷积层自动提取数据的特征,并利用空间共享权重和池化层减少参数量和计算复杂度,成为计算机视觉领域的核心技术。以下是CNN的详细介绍:一、核心思想CNN的核心目标是从图像中自动学习层次化特征,并通过空间共享权重和平移不变性减少参数量和计算成本。其关键组件包括:卷积层(
- ResNet(Residual Network)
不想秃头的程序
神经网络语音识别人工智能深度学习网络残差网络神经网络
ResNet(ResidualNetwork)是深度学习中一种经典的卷积神经网络(CNN)架构,由微软研究院的KaimingHe等人在2015年提出。它通过引入残差连接(SkipConnection)解决了深度神经网络中的梯度消失问题,使得网络可以训练极深的模型(如上百层),并在图像分类、目标检测、语义分割等任务中取得了突破性成果。以下是ResNet的详细介绍:一、核心思想ResNet的核心创新是
- 《现代通信原理与技术》模拟调制与解调—FM 调制实验报告
不想秃头的程序
人工智能matlab信息与通信信号处理
摘要本实验旨在通过MATLAB软件进行模拟调制与解调的实践,加深对频率调制(FrequencyModulation,FM)原理的理解,并掌握FM调制与解调的实现方法。关键词:MATLAB引言在现代通信系统中,调制技术是实现信息传输的核心方法之一。频率调制(FrequencyModulation,FM)作为一种重要的模拟调制方式,通过改变载波信号的频率来传递信息,广泛应用于广播、电视、无线通信等领域
- Spring Batch :高效处理海量数据的利器
一叶飘零_sweeeet
Springbootspringboot
SpringBatch是Spring框架中一个功能强大的批处理框架,旨在帮助开发人员轻松处理大量数据的批量操作,比如数据的导入、导出、转换以及定期的数据清理等任务。它提供了一套完善且灵活的机制,使得原本复杂繁琐的数据批处理工作变得条理清晰、易于管理和扩展。接下来,我们将全方位深入探究SpringBatch,从其核心概念、架构组成,到具体的使用示例以及在不同场景下的应用优势等,带你充分领略它的魅力所
- 平台再升级!接入DeepSeek AI,三大能力一键生成
橙武科技
低代码AIdeepseek人工智能
在数字化项目落地过程中,很多企业都会面临相同的问题:数据库建模要写SQL表结构;业务流程需要画LogicFlow流程图;前端页面还要写AMISJSON配置。从想法到实现,中间至少要经历产品经理、架构师、后端、前端多轮沟通。每个环节都耗时,改起来还要推翻重来。demo地址:https://admin.cwcode.top✨我们的平台,现在直接整合了DeepSeekAI大模型只要输入一句需求,就能:✅
- P25:LSTM实现糖尿病探索与预测
?Agony
lstm人工智能rnn
本文为365天深度学习训练营中的学习记录博客原作者:K同学啊一、相关技术1.LSTM基本概念LSTM(长短期记忆网络)是RNN(循环神经网络)的一种变体,它通过引入特殊的结构来解决传统RNN中的梯度消失和梯度爆炸问题,特别适合处理序列数据。结构组成:遗忘门:决定丢弃哪些信息,通过sigmoid函数输出0-1之间的值,表示保留或遗忘的程度。输入门:决定更新哪些信息,同样通过sigmoid函数控制更新
- 什么是 QueryGPT?智能查询工具如何重塑信息检索的未来?
镜舟科技
StarRocksQueryGPT数据查询数据分析多模态交互
从客户行为数据到供应链信息,从市场趋势到内部运营指标,这些数据蕴含着巨大的商业价值。然而,数据量的激增也带来了前所未有的检索挑战:如何在海量信息中快速定位所需数据?如何确保查询结果的准确性和时效性?据统计,75%的企业正受困于低效的查询工具,这已成为阻碍企业数字化转型的关键痛点。传统的数据查询方式主要依赖SQL语句或特定的查询语言,这要求用户具备专业的编程知识和对数据结构的深入理解。即使对于数据分
- installGo.sh
#!/bin/bash#检查是否以root用户运行if["$(id-u)"-ne0];thenecho"请使用root权限运行此脚本"exit1fi#检查是否安装了必要的工具forcmdincurlwgettar;doif!command-v$cmd&>/dev/null;thenecho"错误:需要安装$cmd"exit1fidone#获取最新版本号echo"正在获取最新Go版本..."LATE
- Python训练营打卡——DAY16(2025.5.5)
cosine2025
Python训练营打卡python开发语言机器学习
目录一、NumPy数组基础笔记1.理解数组的维度(Dimensions)2.NumPy数组与深度学习Tensor的关系3.一维数组(1DArray)4.二维数组(2DArray)5.数组的创建5.1数组的简单创建5.2数组的随机化创建5.3数组的遍历5.4数组的运算6.数组的索引6.1一维数组索引6.2二维数组索引6.3三维数组索引二、SHAP值的深入理解三、总结1.NumPy数组基础总结2.SH
- AI助力基因遗传疾病检测:现状与未来
t0_54program
大数据与人工智能人工智能个人开发
在现代医学领域,与基因紊乱相关疾病的早期检测至关重要。像肺癌,早期诊断的患者5年生存率可达57%,而四期癌症患者生存率仅3%。阿尔茨海默病的早期检测,能让患者改变生活方式、参与临床试验并提前治疗脑部退化症状,有效延长生命。尽管基因检测对评估晚发性阿尔茨海默病的可能性有帮助,对早发性阿尔茨海默病也有指示作用,但其检测技术仍有待完善。目前,仅基于生物学研究的疾病检测技术多样,虽对特定病例精确,但通常需
- Python的一点基础教程------文件读写
卡提西亚
python开发语言
最近在看大佬写的Python教程自学,但是感觉有点头痛,因为大佬讲了一些底层的结构和原理,但是又没那么详细,然后作为一个初学者自学的情况下,看的很费劲.看完就有感而发,想写一篇更基础的教程,教会大家怎么去用它,尽量少的去讲原理.但是当然,你也需要有一定的编程语言基础,了解基本的语法和函数等功能.正所谓师傅领进门,修行在个人,有时候我们学了一个东西,如果觉得很有趣,自然就会去了解关于它的更多信息,但
- 1.2 Python 的特点与优势
Utopia Reverie
pythonpython开发语言
1.语法简洁易读Python以简洁的语法著称,代码可读性强,减少了不必要的符号和冗余代码。例如,使用缩进来表示代码块,而非传统的大括号。这使得代码更易于理解和维护,尤其适合初学者。示例:python运行【#计算斐波那契数列的前10项n=10a,b=0,1for_inrange(n);print(a,end='')a,b=b,a+b#输出:0112358132134】2.开源与社区支持Python是
- apache ftpserver-CentOS config
gengzg
apache
<server xmlns="http://mina.apache.org/ftpserver/spring/v1"
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="
http://mina.apache.o
- 优化MySQL数据库性能的八种方法
AILIKES
sqlmysql
1、选取最适用的字段属性 MySQL可以很好的支持大数据量的存取,但是一般说来,数据库中的表越小,在它上面执行的查询也就会越快。因此,在创建表的时候,为了获得更好的 性能,我们可以将表中字段的宽度设得尽可能小。例如,在定义邮政编码这个字段时,如果将其设置为CHAR(255),显然给数据库增加了不必要的空间,甚至使用VARCHAR这种类型也是多余的,因为CHAR(6)就可以很
- JeeSite 企业信息化快速开发平台
Kai_Ge
JeeSite
JeeSite 企业信息化快速开发平台
平台简介
JeeSite是基于多个优秀的开源项目,高度整合封装而成的高效,高性能,强安全性的开源Java EE快速开发平台。
JeeSite本身是以Spring Framework为核心容器,Spring MVC为模型视图控制器,MyBatis为数据访问层, Apache Shiro为权限授权层,Ehcahe对常用数据进行缓存,Activit为工作流
- 通过Spring Mail Api发送邮件
120153216
邮件main
原文地址:http://www.open-open.com/lib/view/open1346857871615.html
使用Java Mail API来发送邮件也很容易实现,但是最近公司一个同事封装的邮件API实在让我无法接受,于是便打算改用Spring Mail API来发送邮件,顺便记录下这篇文章。 【Spring Mail API】
Spring Mail API都在org.spri
- Pysvn 程序员使用指南
2002wmj
SVN
源文件:http://ju.outofmemory.cn/entry/35762
这是一篇关于pysvn模块的指南.
完整和详细的API请参考 http://pysvn.tigris.org/docs/pysvn_prog_ref.html.
pysvn是操作Subversion版本控制的Python接口模块. 这个API接口可以管理一个工作副本, 查询档案库, 和同步两个.
该
- 在SQLSERVER中查找被阻塞和正在被阻塞的SQL
357029540
SQL Server
SELECT R.session_id AS BlockedSessionID ,
S.session_id AS BlockingSessionID ,
Q1.text AS Block
- Intent 常用的用法备忘
7454103
.netandroidGoogleBlogF#
Intent
应该算是Android中特有的东西。你可以在Intent中指定程序 要执行的动作(比如:view,edit,dial),以及程序执行到该动作时所需要的资料 。都指定好后,只要调用startActivity(),Android系统 会自动寻找最符合你指定要求的应用 程序,并执行该程序。
下面列出几种Intent 的用法
显示网页:
- Spring定时器时间配置
adminjun
spring时间配置定时器
红圈中的值由6个数字组成,中间用空格分隔。第一个数字表示定时任务执行时间的秒,第二个数字表示分钟,第三个数字表示小时,后面三个数字表示日,月,年,< xmlnamespace prefix ="o" ns ="urn:schemas-microsoft-com:office:office" />
测试的时候,由于是每天定时执行,所以后面三个数
- POJ 2421 Constructing Roads 最小生成树
aijuans
最小生成树
来源:http://poj.org/problem?id=2421
题意:还是给你n个点,然后求最小生成树。特殊之处在于有一些点之间已经连上了边。
思路:对于已经有边的点,特殊标记一下,加边的时候把这些边的权值赋值为0即可。这样就可以既保证这些边一定存在,又保证了所求的结果正确。
代码:
#include <iostream>
#include <cstdio>
- 重构笔记——提取方法(Extract Method)
ayaoxinchao
java重构提炼函数局部变量提取方法
提取方法(Extract Method)是最常用的重构手法之一。当看到一个方法过长或者方法很难让人理解其意图的时候,这时候就可以用提取方法这种重构手法。
下面是我学习这个重构手法的笔记:
提取方法看起来好像仅仅是将被提取方法中的一段代码,放到目标方法中。其实,当方法足够复杂的时候,提取方法也会变得复杂。当然,如果提取方法这种重构手法无法进行时,就可能需要选择其他
- 为UILabel添加点击事件
bewithme
UILabel
默认情况下UILabel是不支持点击事件的,网上查了查居然没有一个是完整的答案,现在我提供一个完整的代码。
UILabel *l = [[UILabel alloc] initWithFrame:CGRectMake(60, 0, listV.frame.size.width - 60, listV.frame.size.height)]
- NoSQL数据库之Redis数据库管理(PHP-REDIS实例)
bijian1013
redis数据库NoSQL
一.redis.php
<?php
//实例化
$redis = new Redis();
//连接服务器
$redis->connect("localhost");
//授权
$redis->auth("lamplijie");
//相关操
- SecureCRT使用备注
bingyingao
secureCRT每页行数
SecureCRT日志和卷屏行数设置
一、使用securecrt时,设置自动日志记录功能。
1、在C:\Program Files\SecureCRT\下新建一个文件夹(也就是你的CRT可执行文件的路径),命名为Logs;
2、点击Options -> Global Options -> Default Session -> Edite Default Sett
- 【Scala九】Scala核心三:泛型
bit1129
scala
泛型类
package spark.examples.scala.generics
class GenericClass[K, V](val k: K, val v: V) {
def print() {
println(k + "," + v)
}
}
object GenericClass {
def main(args: Arr
- 素数与音乐
bookjovi
素数数学haskell
由于一直在看haskell,不可避免的接触到了很多数学知识,其中数论最多,如素数,斐波那契数列等,很多在学生时代无法理解的数学现在似乎也能领悟到那么一点。
闲暇之余,从图书馆找了<<The music of primes>>和<<世界数学通史>>读了几遍。其中素数的音乐这本书与软件界熟知的&l
- Java-Collections Framework学习与总结-IdentityHashMap
BrokenDreams
Collections
这篇总结一下java.util.IdentityHashMap。从类名上可以猜到,这个类本质应该还是一个散列表,只是前面有Identity修饰,是一种特殊的HashMap。
简单的说,IdentityHashMap和HashM
- 读《研磨设计模式》-代码笔记-享元模式-Flyweight
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.Collection;
import java.util.HashMap;
import java.util.List;
import java
- PS人像润饰&调色教程集锦
cherishLC
PS
1、仿制图章沿轮廓润饰——柔化图像,凸显轮廓
http://www.howzhi.com/course/retouching/
新建一个透明图层,使用仿制图章不断Alt+鼠标左键选点,设置透明度为21%,大小为修饰区域的1/3左右(比如胳膊宽度的1/3),再沿纹理方向(比如胳膊方向)进行修饰。
所有修饰完成后,对该润饰图层添加噪声,噪声大小应该和
- 更新多个字段的UPDATE语句
crabdave
update
更新多个字段的UPDATE语句
update tableA a
set (a.v1, a.v2, a.v3, a.v4) = --使用括号确定更新的字段范围
- hive实例讲解实现in和not in子句
daizj
hivenot inin
本文转自:http://www.cnblogs.com/ggjucheng/archive/2013/01/03/2842855.html
当前hive不支持 in或not in 中包含查询子句的语法,所以只能通过left join实现。
假设有一个登陆表login(当天登陆记录,只有一个uid),和一个用户注册表regusers(当天注册用户,字段只有一个uid),这两个表都包含
- 一道24点的10+种非人类解法(2,3,10,10)
dsjt
算法
这是人类算24点的方法?!!!
事件缘由:今天晚上突然看到一条24点状态,当时惊为天人,这NM叫人啊?以下是那条状态
朱明西 : 24点,算2 3 10 10,我LX炮狗等面对四张牌痛不欲生,结果跑跑同学扫了一眼说,算出来了,2的10次方减10的3次方。。我草这是人类的算24点啊。。
然后么。。。我就在深夜很得瑟的问室友求室友算
刚出完题,文哥的暴走之旅开始了
5秒后
- 关于YII的菜单插件 CMenu和面包末breadcrumbs路径管理插件的一些使用问题
dcj3sjt126com
yiiframework
在使用 YIi的路径管理工具时,发现了一个问题。 <?php
- 对象与关系之间的矛盾:“阻抗失配”效应[转]
come_for_dream
对象
概述
“阻抗失配”这一词组通常用来描述面向对象应用向传统的关系数据库(RDBMS)存放数据时所遇到的数据表述不一致问题。C++程序员已经被这个问题困扰了好多年,而现在的Java程序员和其它面向对象开发人员也对这个问题深感头痛。
“阻抗失配”产生的原因是因为对象模型与关系模型之间缺乏固有的亲合力。“阻抗失配”所带来的问题包括:类的层次关系必须绑定为关系模式(将对象
- 学习编程那点事
gcq511120594
编程互联网
一年前的夏天,我还在纠结要不要改行,要不要去学php?能学到真本事吗?改行能成功吗?太多的问题,我终于不顾一切,下定决心,辞去了工作,来到传说中的帝都。老师给的乘车方式还算有效,很顺利的就到了学校,赶巧了,正好学校搬到了新校区。先安顿了下来,过了个轻松的周末,第一次到帝都,逛逛吧!
接下来的周一,是我噩梦的开始,学习内容对我这个零基础的人来说,除了勉强完成老师布置的作业外,我已经没有时间和精力去
- Reverse Linked List II
hcx2013
list
Reverse a linked list from position m to n. Do it in-place and in one-pass.
For example:Given 1->2->3->4->5->NULL, m = 2 and n = 4,
return
- Spring4.1新特性——页面自动化测试框架Spring MVC Test HtmlUnit简介
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- Hadoop集群工具distcp
liyonghui160com
1. 环境描述
两个集群:rock 和 stone
rock无kerberos权限认证,stone有要求认证。
1. 从rock复制到stone,采用hdfs
Hadoop distcp -i hdfs://rock-nn:8020/user/cxz/input hdfs://stone-nn:8020/user/cxz/运行在rock端,即源端问题:报版本
- 一个备份MySQL数据库的简单Shell脚本
pda158
mysql脚本
主脚本(用于备份mysql数据库): 该Shell脚本可以自动备份
数据库。只要复制粘贴本脚本到文本编辑器中,输入数据库用户名、密码以及数据库名即可。我备份数据库使用的是mysqlump 命令。后面会对每行脚本命令进行说明。
1. 分别建立目录“backup”和“oldbackup” #mkdir /backup #mkdir /oldbackup
- 300个涵盖IT各方面的免费资源(中)——设计与编码篇
shoothao
IT资源图标库图片库色彩板字体
A. 免费的设计资源
Freebbble:来自于Dribbble的免费的高质量作品。
Dribbble:Dribbble上“免费”的搜索结果——这是巨大的宝藏。
Graphic Burger:每个像素点都做得很细的绝佳的设计资源。
Pixel Buddha:免费和优质资源的专业社区。
Premium Pixels:为那些有创意的人提供免费的素材。
- thrift总结 - 跨语言服务开发
uule
thrift
官网
官网JAVA例子
thrift入门介绍
IBM-Apache Thrift - 可伸缩的跨语言服务开发框架
Thrift入门及Java实例演示
thrift的使用介绍
RPC
POM:
<dependency>
<groupId>org.apache.thrift</groupId>