堆排序详解-Python
堆排序是非常常见考察的一个排序方法,相比于冒泡、选择排序的算法复杂度,堆排序的算法复杂度较低为O(n*log2n);
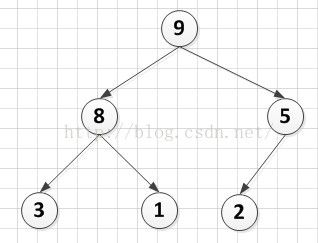
首先堆是一种数据结构,是一棵完全二叉树且满足性质:所有非叶子结点的值均不大于或均不小于其左、右孩子结点的值,如下是一个堆的示例:这是一个大堆
下面我们具体实现一个堆排序的过程(最大堆)
def sift_down(arr, start, end):
root = start # 例子中我们看到第一次root是6这个数
while True:
# 从root开始对最大堆调整
child = 2 * root + 1 # 例子中child对应10这个数
if child > end: # 后面可以看出堆的大小在减小
break
# 找出两个child中较大的一个
if child + 1 <= end and arr[child] < arr[child + 1]:
child += 1
if arr[root] < arr[child]:
# 最大堆root小于较大的child, 交换顺序
arr[root], arr[child] = arr[child], arr[root]
# 正在调整的节点设置为root
root = child
else:
# 无需调整的时候, 退出
break
def heap_sort(arr):
# 从最后一个有子节点的孩子开始调整最大堆 例子中对应 6—10对
first = len(arr) // 2 - 1 # 例子中对应01234 第五个数 角标为4
for start in range(first, -1, -1): # 循环到第4,3,2,1,0个
sift_down(arr, start, len(arr) - 1) # 排序一次的结果
# 将最大的放到堆的最后一个, 堆大小-1, 继续调整排序
for end in range(len(arr) -1, 0, -1): #剩下9次 循环987654321
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1) # 注意start=0
def main():
# [7, 95, 73, 65, 60, 77, 28, 62, 43]
# [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
print l
heap_sort(l) #调用
print l
if __name__ == "__main__":
main()
[3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]