排序在编程的过程中是非常重要的一类算法。一个好的排序算法可以让我们整体的算法效率提高很多,但是不同的排序算法实现起来的难度也有比较大的差别。那么现在具体来看一下各个排序算法的主要思想。
1、直接插入排序
算法思想:
-
排序区间 R[1..n] ;
-
在排序的过程中,整个排序区间被分为两个子区间: 有序区 R[1..i-1] 和无序区 R[ i ..n] ;
-
共进行 n - 1 趟排序,每趟排序都是把无序区的 第一条记录 R i 插到有序区的合适位置上;
代码实现:
/*直接插入排序*/
void InsertSort(KeyType R[], int n)
{
int i, j;
KeyType tmp;
for (i = 1; i= 0 && tmp 性能分析:
2、折半插入排序
算法思想:
折半插入排序是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
在将一个新元素插入已排好序的数组的过程中,寻找插入点时,将待插入区域的首元素设置为a[low],末元素设置为a[high],则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素小,则选择a[low]到a[m-1]为新的插入区域(即high=m-1),否则选择a[m+1]到a[high]为新的插入区域(即low=m+1),如此直至low<=high不成立,即将此位置之后所有元素后移一位,并将新元素插入a[high+1]。
代码实现:
/*折半插入排序*/
void InsertSort1(KeyType R[], int n)
{
int i, j, low, high, mid;
int tmp;
for (i = 1; i= high + 1; j--) //元素后移
R[j + 1] = R[j];
R[high + 1] = tmp; //插入
}
}
折半插入排序算法是一种稳定的排序算法,比直接插入算法明显减少了关键字之间比较的次数,因此速度比直接插入排序算法快,但记录移动的次数没有变,所以折半插入排序算法的时间复杂度仍然为O(n^2),与直接插入排序算法相同。附加空间O(1)。
3、希尔排序
算法思想:
- 在排序的过程中,整个排序区间被分为几个子表;
- 对每个子表分别进行直接插入排序;
- 由于n2>n12+n22+…+nk2 ( n=n1+n2+…+nk)
所以对每个子表排序所耗费的时间之和要小于对整个区间排序所耗费的时间;
- 通过对子表小范围的排序,将排序区间调整成基本有序的序列;
- 不断减少子表的个数(即扩大子表的长度), 直至子表的个数为1, 完成整个排序操作。

算法实现:
/*希尔排序算法*/
void ShellSort(KeyType R[], int n)
{
int i, j, gap;
KeyType tmp;
gap = n / 2; //增量置初值
while (gap>0)
{
for (i = gap; i= 0 && tmp
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小,插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比o(n^2)好一些。
4、冒泡排序
算法思想:
-
自下而上 ( 或上而下 ) 扫描记录序列;
-
相邻的两条记录 R i 与 R i - 1 ( 或 R i+1 ) 如果是逆序;
-
则交换位置。

代码实现:
/*冒泡排序算法*/
void BubbleSort(KeyType R[], int n)
{
int i, j;
bool exchange;
KeyType tmp;
for (i = 0; ii; j--) //比较,找出最小关键字的元素
if (R[j] 
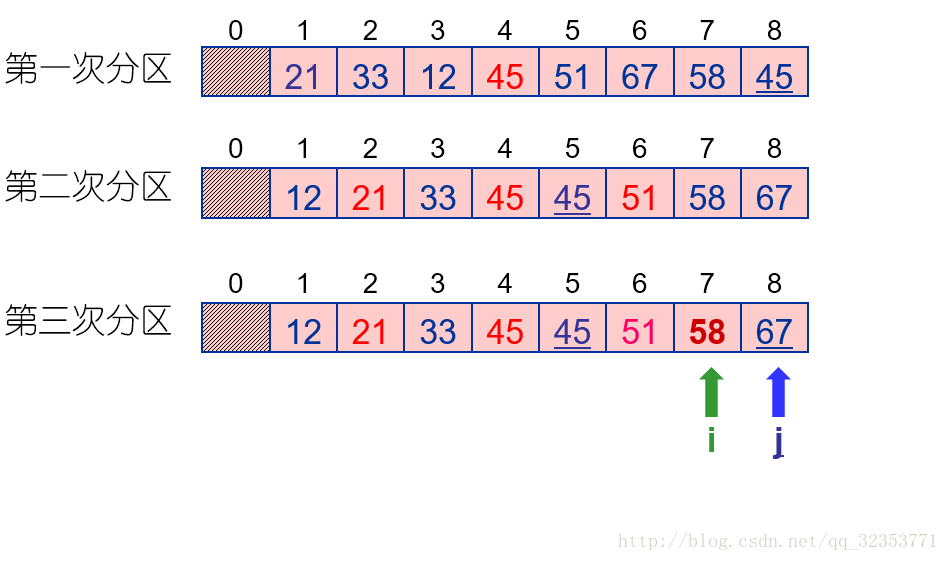
5、快速排序
算法思想:
-
设排序区间为 R[ low . . high ] ;
-
在排序区间任选一个记录 Rx 做为基准;
-
经过一趟排序后,将排序区间分为左、右两个子区间:
R[low . . i-1 ] Rx R[i+1 . . high ];
-
使得: R[ low. .i-1 ].key ≤ Rx.key ≤ R [ i+1. .high ].key;
-
然后再用相同的方法分别对左、右区间进行排序,直至每个区间长度都是 1 为止。
代码实现:
/*快速排序算法*/
void QuickSort(KeyType R[], int s, int t)
{
int i = s, j = t;
KeyType tmp;
if (si && R[j] >= tmp)
j--; //从右向左扫描,找第1个小于tmp的R[j]
R[i] = R[j]; //找到这样的R[j],R[i]和R[j]交换
while (i 
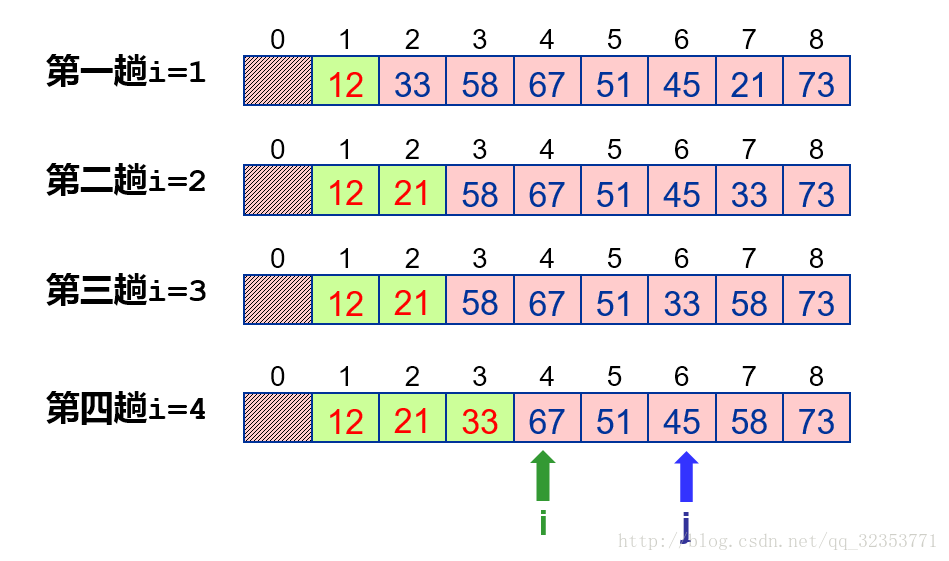
6、直接选择排序
算法思想:
-
设:排序区间 R[1..n] ;
-
在排序的过程中,整个排序区间被分为两个子区间:有序区 R[1..i-1] 和无序区 R[ i ..n] ;
-
共进行 n - 1 趟排序,每趟排序都是选择无序区的最小记录 R min ;将 R min 与无序区的第一条记录位置互换,使得无序区长度减 1 ,有序区长度增 1 。
代码实现:
/*直接选择排序*/
void SelectSort(KeyType R[], int n)
{
int i, j, k;
KeyType tmp;
for (i = 0; i
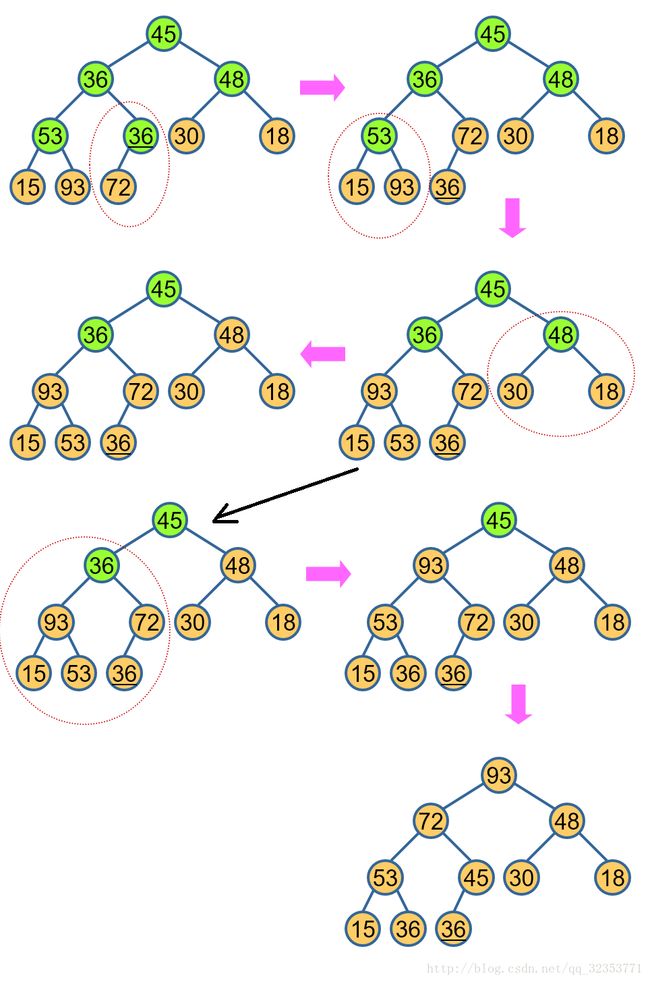
7、堆排序
算法思想:
-
回顾完全二叉树的性质;
-
编号为 i 的结点 , 其左孩子的编号为 2i, 右孩子的编号为 2i+1;
-
如果将堆序列看成完全二叉树的按层次遍历序列;
-
则这棵完全二叉树上每个结点的值比左孩子和右孩子值都要大 ( 大根堆 ), 或比左孩子和右孩子值都要小 ( 小根堆 ) 。
代码实现:
/*堆排序算法*/
void sift(KeyType R[], int low, int high)
{
int i = low, j = 2 * i; //R[j]是R[i]的左孩子
KeyType tmp = R[i];
while (j <= high)
{
if (j= 1; i--) //循环建立初始堆
sift(R, i, n);
for (i = n; i >= 2; i--) //进行n-1趟完成推排序,每一趟堆排序的元素个数减1
{
tmp = R[1]; //将最后一个元素同当前区间内R[1]对换
R[1] = R[i];
R[i] = tmp;
sift(R, 1, i - 1); //筛选R[1]节点,得到i-1个节点的堆
}
}
算法思想:
-
一种基于将两个有序表异地归并成一个有序表的排序策略。
-
初态是将排序表中的每个元素看成是一个有序的子表,共有 n 个子表。
25 57 48 37 12 92 86 72 31 48
[25] [92] [48] [37] [12] [57] [86] [72] [31] [48]
-
经过一趟排序,将两个相邻的有序子表归异地并成一个有序子表;
-
共进行 log 2 n 趟这样的归并,整个排序表就被归并成了一个有序表。

代码实现:
/*二路归并排序算法*/
void Merge(KeyType R[], int low, int mid, int high)
{
KeyType *R1;
int i = low, j = mid + 1, k = 0; //k是R1的下标,i、j分别为第1、2段的下标
R1 = (KeyType *)malloc((high - low + 1) * sizeof(KeyType)); //动态分配空间
while (i <= mid && j <= high) //在第1段和第2段均未扫描完时循环
if (R[i] <= R[j]) //将第1段中的元素放入R1中
{
R1[k] = R[i];
i++; k++;
}
else //将第2段中的元素放入R1中
{
R1[k] = R[j];
j++; k++;
}
while (i <= mid) //将第1段余下部分复制到R1
{
R1[k] = R[i];
i++; k++;
}
while (j <= high) //将第2段余下部分复制到R1
{
R1[k] = R[j];
j++; k++;
}
for (k = 0, i = low; i <= high; k++, i++) //将R1复制回R中
R[i] = R1[k];
free(R1);
}
/*对整个数序进行一趟归并*/
void MergePass(KeyType R[], int length, int n)
{
int i;
for (i = 0; i + 2 * length - 1完整代码:
#include
#include
#include
#include
#define MaxSize 50001
typedef int KeyType;
/*产生R[low..high中的随机数*/
void initial(int R[], int low, int high)
{
int i;
srand((unsigned)time(NULL));
for (i = low; iR[i + 1])
return false;
return true;
}
/*求时间差*/
void Difference(struct _timeb timebuf1, struct _timeb timebuf2)
{
long s, ms;
s = timebuf2.time - timebuf1.time; //两时间相差的秒数
ms = timebuf2.millitm - timebuf1.millitm; //两时间相差的毫秒数
if (ms<0)
{
s--;
ms = 1000 + ms;
}
printf("%d秒%d毫秒", s, ms);
}
/*直接插入排序*/
void InsertSort(KeyType R[], int n)
{
int i, j;
KeyType tmp;
for (i = 1; i= 0 && tmp= high + 1; j--) //元素后移
R[j + 1] = R[j];
R[high + 1] = tmp; //插入
}
}
/*求折半插入排序的时间*/
void InsertSort1Time()
{
KeyType R[MaxSize];
int n = 50000;
struct _timeb timebuf1, timebuf2;
printf("折半插入排序\t");
initial(R, 0, n - 1);
_ftime(&timebuf1);
InsertSort1(R, n);
_ftime(&timebuf2);
Difference(timebuf1, timebuf2);
if (test(R, 0, n - 1))
printf("\t正确\n");
else
printf("\t错误\n");
}
/*希尔排序算法*/
void ShellSort(KeyType R[], int n)
{
int i, j, gap;
KeyType tmp;
gap = n / 2; //增量置初值
while (gap>0)
{
for (i = gap; i= 0 && tmpi; j--) //比较,找出最小关键字的元素
if (R[j]i && R[j] >= tmp)
j--; //从右向左扫描,找第1个小于tmp的R[j]
R[i] = R[j]; //找到这样的R[j],R[i]和R[j]交换
while (i= 1; i--) //循环建立初始堆
sift(R, i, n);
for (i = n; i >= 2; i--) //进行n-1趟完成推排序,每一趟堆排序的元素个数减1
{
tmp = R[1]; //将最后一个元素同当前区间内R[1]对换
R[1] = R[i];
R[i] = tmp;
sift(R, 1, i - 1); //筛选R[1]节点,得到i-1个节点的堆
}
}
/*求堆排序算法的时间*/
void HeapSortTime()
{
KeyType R[MaxSize];
int n = 50000;
struct _timeb timebuf1, timebuf2;
printf("堆 排 序\t");
initial(R, 1, n);
_ftime(&timebuf1);
HeapSort(R, n);
_ftime(&timebuf2);
Difference(timebuf1, timebuf2);
if (test(R, 1, n))
printf("\t正确\n");
else
printf("\t错误\n");
}
/*二路归并排序算法*/
void Merge(KeyType R[], int low, int mid, int high)
{
KeyType *R1;
int i = low, j = mid + 1, k = 0; //k是R1的下标,i、j分别为第1、2段的下标
R1 = (KeyType *)malloc((high - low + 1) * sizeof(KeyType)); //动态分配空间
while (i <= mid && j <= high) //在第1段和第2段均未扫描完时循环
if (R[i] <= R[j]) //将第1段中的元素放入R1中
{
R1[k] = R[i];
i++; k++;
}
else //将第2段中的元素放入R1中
{
R1[k] = R[j];
j++; k++;
}
while (i <= mid) //将第1段余下部分复制到R1
{
R1[k] = R[i];
i++; k++;
}
while (j <= high) //将第2段余下部分复制到R1
{
R1[k] = R[j];
j++; k++;
}
for (k = 0, i = low; i <= high; k++, i++) //将R1复制回R中
R[i] = R1[k];
free(R1);
}
/*对整个数序进行一趟归并*/
void MergePass(KeyType R[], int length, int n)
{
int i;
for (i = 0; i + 2 * length - 1 
