LQR,iLQR,DDP控制论经典算法（MBRL基础知识）

一、线性二次型调节器LQR（Linear Quadratic Regulator）

1.1 LQR符号与术语

现有一些随机策略$p_{\theta }(u_t|x_t)$收集的样本：
$${\tau }^i=(x_1^i,u_1^i,x_2^i,u_2^i,...,x_T^i,u_T^i,x_{T+1}^i),i=1,2...,N$$
$x_t,u_t$即为第t时刻的状态与动作，此为控制论符号的表述$(x_t,u_t)=(s_t,a_t)$，两者可进行混用。lec1-lec4中提到，NN的cost function $c(x_t,u_t)$实际上是一种immediate的监督信号，RL的reward function $r(s_t,a_t)$实际上是一种delayed的监督信息，因此在一个time step下，有$c(x_t,u_t)=-r(x_t,u_t)+constant$。下面给出一个术语表格，基础知识主要使用控制领域的术语表述。

	Control	RL
状态state	$x_t$	$s_t$
动作action	$u_t$	$a_t$
监督信号	$c(x_t,u_t)$	$r(s_t,a_t)$
动态模型	$x_{t+1}\sim f(x_t,u_t)$	$s^{\prime }\sim p(s^{\prime }｜s,a)$

1.2 LQR问题下的设定

1. 动态模型是deterministic的，即$x_{t+1}=f(x_t,u_t),f(x_t,u_t)$不是一个概率分布的模型。

2. 监督信号cost function，最优控制中有performance measure的指标$J=h(x_T,T)+{\int }_{t_{=}0}^{T}g(x_t,u_t,t)dt$，第一项衡量该轨迹$\tau$末尾的状态$X_T$与任务目标状态的距离，第二项衡量该轨迹$\tau$从起始到末尾，走完该轨迹中每个状态与动作所要消耗的代价，其中函数g为标量。因此$c(x_t,u_t)$即为performace measure中的函数g。LQR的监督信号$c(x_t,u_t)$是已知的，输入$x_t,u_t$，输出一个标量scalar。

3. LQR的目的是，给定一个初始状态$x_1$，终止状态或任务目标状态$x_{T+1}$，已知环境动态模型$x_{t+1}=f(x_t,u_t)$，求出一串动作序列$u_1,u_2,...,u_T$使得累积cost最小，即
   $$\underset{u1,...,u_T}{\min }\sum _{t=1}^{T}c(x_t,u_t)s.t{x}_t=f(x_{t-1},u_{t-1})$$

4. LQR的approximation，linear体现在对$f(x_t,u_t)$采用一阶线性近似，quadratic体现在对$c(x_t,u_t)$采用二阶近似，即
   $$\begin{gathered} x_{t+1}=f(x_t,u_t)\approx F_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+f_t=\left[\begin{array}{cc}{F}_{x_t}& F_{u_t}\end{array}\right]\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+f_t \\ c(x_t,u_t)=\frac{1}{2}{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T\left[\begin{array}{cc}{C}_{x_t,x_t}& C_{x_t,u_t}\\ C_{u_t,x_t}& C_{u_t,u_t}\end{array}\right]\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T\left[\begin{array}{c}{c}_{x_t}\\ c_{u_t}\end{array}\right]=\frac{1}{2}{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T{C}_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T{c}_t \end{gathered}$$
   所以LQR的优化问题表述为：
   $$\begin{gathered} \underset{u1,...,u_T}{\min }\sum _{t=1}^{T}c(x_t,u_t)s.t{x}_t=f(x_{t-1},u_{t-1}) \\ f(x_t,u_t)=F_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+f_t \\ c(x_t,u_t)=\frac{1}{2}{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T{C}_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T{c}_t \end{gathered}$$
   其中$F_t,f_t,C_t,c_t$均已知，下面推到用到其展开形式！

1.3 LQR求解

LQR求解主要有Backward Pass与Forward Pass两大过程，先看看对于LQR这个问题，什么是已知的，什么是未知的。

• 已知：initial state 初始状态$x_1$,goal state目标状态$x_{T+1}$,动态模型$f(x_t,u_t)$与cost function $c(x_t,u_t)$的结构参数$F_t,f_t,C_t,c_t$
• 未知：$x_2,x_3,...,x_T,u_1,u_2,...,u_T$。因为$x_2=f(x_1,u_1),x_3=f(x_2,u_2),...,x_T=f(x_{T-1},u_{T-1}),x_{T+1}=f(x_T,u_T)$，所以实际上未知的就是动作序列$u_1,...,u_T$
• 目标函数变为：${\min }_{u_1,..u_T}c(x_1,u_1)+c(f(x_1,u_1),u_2)+\cdots +c(f(f(...()...),u_T)$啰嗦一下，$V(x_{T+1})$由于终态确定，故可看做$const$，而且dynamics是deterministic的，所以有$Q(x_t,u_t)=r(x_t,u_t)+V(x_{t+1})$，于是目标函数可以看成：
  $$\begin{array}{rl}& \underset{u_1,..u_T}{\min }c(x_1,u_1)+c(f(x_1,u_1),u_2)+\cdots +c(f(f(...()...),u_T)-V(x_{T+1})\\ & \underset{u_1,...,u_T}{\max }r(x_1,u_1)+r(f(x_1,u_2),u_2)+\cdots +\underset{Q}{r(x_T,u_T)+V(x_{T+1})}\\ =& \underset{u_1,...,u_T}{\max }r(x_1,u_1)+r(f(x_1,u_2),u_2)+\cdots +r(x_{T-1},u_{T-1})+\underset{u_T=K_T{x}_T+k_T}{Q(x_T,u_T)}\\ =& \underset{u_1,...,u_T}{\max }r(x_1,u_1)+r(f(x_1,u_2),u_2)+\cdots +r(x_{T-1},u_{T-1})+V(x_T,u_T)\\ =& \underset{u_1,...,u_T}{\max }r(x_1,u_1)+r(f(x_1,u_2),u_2)+\cdots +Q(x_{T-1},u_{T-1})\\ =& \underset{u_1,...,u_T}{\max }Q(x_1,u_1)\end{array}$$
  求解思路，固定一个变量，调整其它变量，一个个求嘛，但如果是固定$u_1$，即Forward Pass前向算法，会经过多个动态模型$f$的迭代，很难求解，于是先从BackWard角度考虑，即从$u_T$入手。

1.3.1 推导过程

• $c(x_T,u_T)$是一个二元函数，真正未知的只有$u_T$，要使cost最小，所以对其求导，得到$u_T$关于$x_T$的关系，称作控制律，是在Backward pass中实际想要的东西。
  $$\begin{array}{rl}{\nabla }_{u_T}Q(x_T,u_T)={\nabla }_{u_T}c(x_T,u_T)& ={\nabla }_{u_T}[\frac{1}{2}{\left[\begin{array}{c}{x}_T\\ u_T\end{array}\right]}^T{C}_T\left[\begin{array}{c}{x}_T\\ u_T\end{array}\right]+{\left[\begin{array}{c}{x}_T\\ u_T\end{array}\right]}^T{c}_T]\\ & ={\nabla }_{u_T}[C_{x_T,u_T}{x}_T+C_{u_T,u_T}{u}_T+c_{u_T}]）\\ & =0\\ 所以u_T& =-C_{u_T,u_T}^{-1}(C_{u_T,x_T}{x}_T+c_{u_T})\end{array}$$
  换一下表述有：
  $$\begin{gathered} u_T=K_T{x}_T+k_T \\ {K}_T=-C_{u_T,u_T}^{-1}{C}_{u_T,x_T},k_T=-C_{u_T,u_T}^{-1}{c}_{u_T} \end{gathered}$$
  这一步，得到了第T时刻的动作$u_T$与第T时刻的状态$x_T$之间的关系，其它系数均已知。

• 再看$u_{T-1}$时，由动态模型$x_T=f(x_{T-1},u_{T-1})$，由Q值函数$Q(x_{T-1},u_{T-1})=r(x_{T-1},u_{T-1})+V(x_T)=-c(x_{T-1},u_{T-1})+V(x_T)$。
  实际上，回顾lec5-lec9中对$Q(s,a)$与$V(s)$的理解，有$Q(x_T,u_T)=r(x_T,u_T)+E[V(x_{T+1})]=r(x_T,u_T)+const=-c(x_T,u_T)+const$，代入$u_T=K_T{x}_T+k_T$，则：
  $$V(x_T)=Q(x_T,K_T{x}_T+k_T)=-c(x_T,K_T{x}_T+k_T)+const$$代入quadratic cost function后化简一下并替换下表述有：
  $$\begin{array}{rl}& V(x_T)=-\frac{1}{2}{x}_T^T{V}_T{x}_T+x_T^T{v}_T\\ V_T& =C_{x_T,x_T}+C_{x_T,u_T}{K}_T+K_T^T{C}_{u_T,x_T}+K_T^T{C}_{u_T,u_T}{K}_T\\ v_T& =c_{x_T}+C_{x_T,u_T}{k}_T+K_T^T{C}_{u_T}+K_T^T{C}_{u_T,u_T}{k}_T\end{array}$$
  因此，表示T-1时刻的Q值函数，利用动态模型消掉$x_T$并使其导数为0。
  $$\begin{array}{rl}-Q(x_{T-1},u_{T-1})& =c(x_{T-1},u_{T-1})-V(x_T)\\ & =\frac{1}{2}{\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]}^T{C}_{T-1}\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]+{\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]}^T{c}_{T-1}+\frac{1}{2}{x}_T^T{V}_T{x}_T+x_T^T{v}_T\end{array}$$
  代入$x_T=f(x_{T-1},u_{T-1})=F_{T-1}\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]+f_{T-1}$，便得到了仅有$x_{T-1},u_{T-1}$表示的$Q(x_{T-1},u_{T-1})$
  具体而言，经过整理：
  $$\begin{gathered} Q(x_{T-1},u_{T-1})=\frac{1}{2}{\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]}^T{Q}_{T-1}\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]+{\left[\begin{array}{c}{x}_{T-1}\\ u_{T-1}\end{array}\right]}^T{q}_{T-1} \\ \begin{array}{rl}& Q_{T-1}=C_{T-1}+F_{T-1}^T{V}_T{F}_{T-1}\\ & q_{T-1}=c_{T-1}+F_{T-1}^T{V}_T{f}_{T-1}+F_{T-1}^T{v}_T\end{array} \end{gathered}$$
  令其导数为0，得到$u_{T-1}$与$x_{T-1}$的关系，即T-1时刻的控制律：
  $$\begin{gathered} {\nabla }_{u_{T-1}}Q(x_{T-1},u_{T-1})=0 \\ {u}_{T-1}=K_{T-1}{x}_{T-1}+k_{T-1} \\ {K}_{T-1}=-Q_{u_{T-1},u_{T-1}}^{-1}{Q}_{u_{T-1},x_{T-1}},k_{T-1}=-Q_{u_{T-1},u_{T-1}}^{-1}{q}_{u_{T-1}} \end{gathered}$$

• 如此类推，Backward Pass得到动作与状态的控制律：
  $$u_t=K_t{x}_t+k_t,t=1,2,...,T$$

  又因为$x_1$已知，所以$u_1$可由$u_1=K_1{x}_1+k_1$计算得出，于是Forward Pass结合动态模型，算出动作序列：
  $$\begin{gathered} x_2=f(x_1,u_1) \\ {u}_2=K_2{x}_2+k_2 \\ {x}_3=f(x_2,u_2) \\ ⋮ \\ {u}_T=K_T{x}_T+k_T \end{gathered}$$

• 小总结

Backward Pass步骤：

1. T时刻的${\nabla }_{u_T}Q(x_T,u_T)=0$，得控制律$u_T=K_T{x}_T+k_T$
2. 计算$V(x_T)$，并利用$x_T=f(x_{T-1},u_{T-1})$消元，从而得到$Q(x_{T-1},u_{T-1})=-c(x_{T-1},u_{T-1})+V(x_T)=-c(x_{T-1},u_{T-1})+V(f(x_{T-1},u_{T-1}))$
3. ${\nabla }_{u_T}Q(x_T,u_T)=0$，得控制律$u_{T-1}=K_{T-1}{x}_{T-1}+k_{T-1}$
4. 计算$V(x_{T-1})$，利用动态模型消元，得$Q(x_{T-2},u_{T-2})$
5. ${\nabla }_{u_{T-2}}Q(x_{T-2},u_{T-2}))=0$，得控制律$u_{T-2}=K_{T-2}{x}_{T-2}+k_{T-2}$
6. 以此类推。

Forward Pass步骤：
利用动态模型计算下一状态，利用控制律，计算出相应动作

1.3.2 LQR算法流程

• Backward Pass
  for t=T to t=1:
  $$\begin{array}{rl}& Q_t=C_t+F_t^T{V}_{t+1}{F}_t\\ & q_t=c_t+F_t^T{V}_{t+1}{f}_t+F_t^T{v}_{t+1}\\ & Q\left(x_t,u_t\right)=const+\frac{1}{2}{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T{Q}_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+{\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}^T{q}_t\\ & u_t\leftarrow \arg \underset{u_t}{\min }Q\left(x_t,u_t\right)=K_t{x}_t+k_t\\ & K_t=-Q_{u_t,u_t}^{-1}{Q}_{u_t,x_t}\\ & k_t=-Q_{u_t,u_t}^{-1}{q}_{u_t}\\ & V_t=Q_{x_t,x_t}+Q_{x_t,u_t}{K}_t+K_t^T{Q}_{u_t,x_t}+K_t^T{Q}_{u_t,u_t}{K}_t\\ & v_t=q_{x_t}+Q_{x_t,u_t}{k}_t+K_t^T{Q}_{u_t}+K_t^T{Q}_{u_t,u_t}{k}_t\\ & V\left(x_t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}+\frac{1}{2}{x}_t^T{V}_t{x}_t+x_t^T{v}_t\end{array}$$
• Forward Pass
  for t=1 to t=T:
  $$\begin{array}{rl}& u_t=K_t{x}_t+k_t\\ & x_{t+1}=f\left(x_t,u_t\right)\end{array}$$
• LQR模块
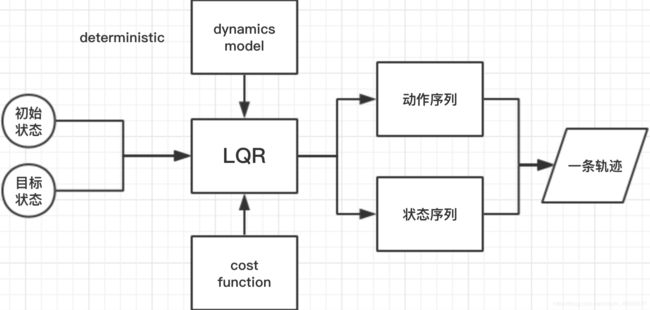
  即使上述过程不是很透彻，亦可如下图所示将LQR看成一个黑盒模块，对于已知deterministic的dynamics，使用LQR算法，便可得到一组动作序列$u_1,...,u_T$，并可计算出状态序列。
  输入：初始状态$x_1$，目标状态$x_{T+1}$，动态模型$f(x_t,u_t)$，代价函数$c(x_t,u_t)$
  输出：动作序列$u_1,...,u_T$和状态序列$x_1,...,x_T$，即一条轨迹
  

二、iLQR（Iterative Linear Quadratic Regulator）

LQR的linear dynamics是deterministic的，这非常受限，对应RL中的$s^{\prime }=p(s^{\prime }|s,a)$，在当前state，选择一个action后，下一状态就确定了。为了应对复杂环境dynamics的stochastic，即$s^{\prime }\sim p(s^{\prime }|s,a)$，相当于说把LQR中假设linear dynamics拓展成了Non-linear dynamics，这时候需要采用iLQR，再叙述之前，先回顾一下以下两种优化算法，可参考以下专栏。
优化算法（甩甩的知乎专栏）

2.1 Newton Method

寻找参数$\theta$最小化损失函数
$$minL(\theta )$$

在参数空间初始化一个参数$\hat{\theta }$，寻找一个增量$\Delta \theta$，采用泰勒二阶近似：
$$L(\hat{\theta }+\Delta \theta )\approx \hat{L}(\hat{\theta }+\Delta \theta )=L(\hat{\theta })+\nabla L(\hat{\theta }{)}^T\Delta \theta +\frac{1}{2}(\Delta \theta {)}^T{\nabla }^{2}L(\hat{\theta })\Delta \theta$$

寻找的增量$\Delta \theta$使得$L(\hat{\theta }+\Delta \theta )$最小，即$L(\hat{\theta }+\Delta \theta )\le L(\hat{\theta })$且${\nabla }_{\Delta \theta }L(\hat{\theta }+\Delta \theta )=0$所以有：
$${\nabla }_{\Delta \theta }(L(\hat{\theta })+\nabla L(\hat{\theta }{)}^T\Delta \theta +\frac{1}{2}(\Delta \theta {)}^T{\nabla }^{2}L(\hat{\theta })\Delta \theta )\approx 0$$

下面将符号稍微写繁琐一点，实际上$\nabla L(\hat{\theta })$为Jacobian矩阵$J(\hat{\theta })$，${\nabla }^{2}L(\hat{\theta })$为Hessian矩阵$H(\hat{\theta })$
$${\nabla }_{\hat{\theta }}L(\hat{\theta })+{\nabla }_{\hat{\theta }}^{2}L(\hat{\theta })\Delta \theta \approx 0$$

$$\begin{gathered} \Delta \theta \approx -({\nabla }_{\hat{\theta }}^{2}L(\hat{\theta }){)}^{-1}{\nabla }_{\hat{\theta }}L(\hat{\theta })=-H(\hat{\theta }{)}^{-1}J(\hat{\theta }) \\ {\theta }_{t+1}={\theta }_t+\Delta {\theta }_t\approx {\theta }_t-H_t^{-1}{J}_t \end{gathered}$$
所以Newton Method的更新策略为：
$$\begin{gathered} J_t=\nabla L({\theta }_t) \\ {H}_t={\nabla }^{2}L({\theta }_t) \\ {\Delta }_t=-H_t^{-1}{J}_t \\ {\alpha }_t=\underset{\alpha >0}{\mathrm{argmin}}L({\theta }_t+\alpha {\Delta }_t)LineSearch! \\ {\theta }_{t+1}={\theta }_t+{\alpha }_t{\Delta }_t \end{gathered}$$
上述更新策略，有一个line search的过程。通过$g$表示gradient，$x$替换$\theta$，$\hat{x}$为更新前的值，亦可简化表述为iLQR需要用到的形式，如下：
Until convergence:
$$\begin{gathered} g={\nabla }_{x}L(\hat{x}) \\ H={\nabla }_x^{2}L(\hat{x}) \\ \hat{x}\leftarrow \underset{x}{\mathrm{argmin}}L(x)-L(\hat{x})\approx \frac{1}{2}(x-\hat{x}{)}^{T}H(x-\hat{x})+g^T(x-\hat{x}) \end{gathered}$$

2.2 Gauss-Newton Method

因为牛顿方法中不仅要求Hessian矩阵，而且还要求它的逆，计算复杂度猛增，许多拟牛顿方法就是通过不同方式去逼近Hessian矩阵的逆。而高斯牛顿方法实际上，是在最小二乘法中的特殊求解，用一阶梯度的信息来逼近Hessian矩阵
$$H^{-1}\approx (J^{T}J{)}^{-1}$$

2.3 iLQR算法

iLQR背景设定

• dynamics model
  iLQR的特点是能处理non-linear，stochastic的dynamics model，其模型结构，可从LQR简化为：
  $$LQR:f(x_t,u_t)=F_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+f_t$$

$$iLQR:f(x_t,u_t)=N(F_t\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]+f_t,{\Sigma }_t)$$

• LQR
  LQR的约束，是一个线性系统，可通过deterministic的dynamics model确定下一状态$x_{t+1}$与当前状态$x_t$、动作$u_t$的关系，cost也可以由$x_t,u_t$确定。
  $$\begin{array}{rl}& f\left(x_t,u_t\right)=F_t\left[\begin{array}{l}{x}_t\\ u_t\end{array}\right]+f_t\\ & c\left(x_t,u_t\right)=\frac{1}{2}{\left[\begin{array}{l}{x}_t\\ u_t\end{array}\right]}^T{C}_t\left[\begin{array}{l}{x}_t\\ u_t\end{array}\right]+{\left[\begin{array}{l}{x}_t\\ u_t\end{array}\right]}^T{c}_t\end{array}$$
• iLQR
  iLQR的dynamics是非线性的，即下一状态$x_{t+1}$不能靠当前状态$x_t$、当前动作$u_t$线性关系确定，可理解为利用泰勒展开逼近两状态间$x_t,x_{t+1}$假设的高斯分布，对dynamics一阶泰勒近似，对cost二阶泰勒近似，如下：
  $$\begin{array}{rl}& f\left(x_t,u_t\right)\approx f\left({\hat{x}}_t,{\hat{u}}_t\right)+{\nabla }_{x_t,u_t}f\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{l}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]\\ & c\left(x_t,u_t\right)\approx c\left({\hat{x}}_t,{\hat{u}}_t\right)+{\nabla }_{x_t,u_t}c\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{c}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]+\frac{1}{2}{\left[\begin{array}{c}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]}^T{\nabla }_{x_t,u_t}^{2}c\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{l}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]\end{array}$$

iLQR流程

整理一下有：
$$\begin{array}{rl}& f\left(x_t,u_t\right)-f\left({\hat{x}}_t,{\hat{u}}_t\right)\approx {\nabla }_{x_t,u_t}f\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{l}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]\\ & c\left(x_t,u_t\right)-c\left({\hat{x}}_t,{\hat{u}}_t\right)\approx {\nabla }_{x_t,u_t}c\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{c}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]+\frac{1}{2}{\left[\begin{array}{c}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]}^T{\nabla }_{x_t,u_t}^{2}c\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{l}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]\end{array}$$

更换一下表述$\delta x_t=x_t-{\hat{x}}_t,\delta u_t=u_t-{\hat{u}}_t$：
$$\bar{f}(\delta x_t,\delta u_t)=f\left(x_t,u_t\right)-f\left({\hat{x}}_t,{\hat{u}}_t\right)\approx {\nabla }_{x_t,u_t}f\left({\hat{x}}_t,{\hat{u}}_t\right)\left[\begin{array}{l}{x}_t-{\hat{x}}_t\\ u_t-{\hat{u}}_t\end{array}\right]=F_t\left[\begin{array}{l}\delta x_t\\ \delta u_t\end{array}\right]$$

c ˉ ( δ x t , δ u t ) = c ( x t , u t ) − c ( x ^ t , u ^ t ) ≈ ∇ x t , u t c ( x ^ t , u ^ t ) [ x t − x ^ t u t − u ^ t ] + 1 2 [ x t − x ^ t u t − u ^ t ] T ∇ x t , u t 2 c ( x ^ t , u ^ t ) [ x t − x ^ t u t − u ^ t ] = c t [ δ x t δ u t ] + 1 2 [ δ x t δ u t ] T C t [ δ x t δ u t ] \begin{aligned} \bar{c}(\delta x_t,\delta u_t)