gurobi的申请+安装

• 开代理
• 网址：https://www.gurobi.com

 

• 注册
  1. My account的位置有register，点击注册，输入注册信息
  2. 

 

• 1. 登录，点击同样位置的login
• 申请licence（download&licence->academic license）
  1. 
  2. 复制licence
  3. 

 

• 下载软件
  1. download&licence->download center->Gurobi Optimizer
  2. 
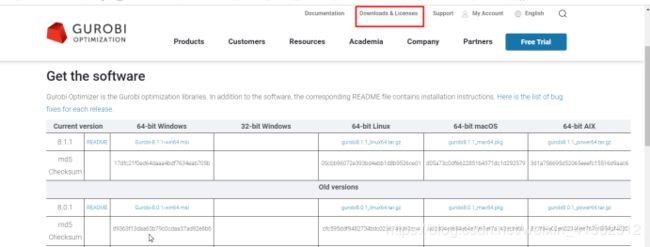
  3. 选择版本
• 安装gurobi
  1. 全都默认就可以，可以自己改安装路径
  2. 安装完了重启（安装默认修改了环境变量）
• 打开软件输入grbgetkey
  1. 
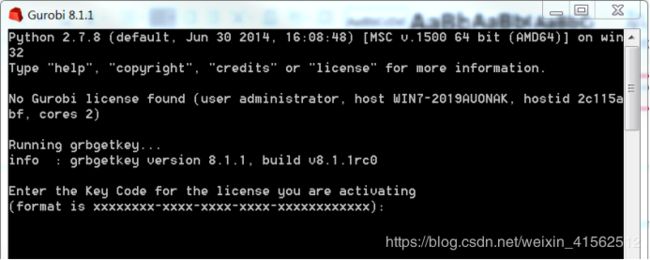
  2. 操作完软件会退出，再次打开
  3. 
• 安装anaconda（网上很多，就不写了）
  1. 只说一点问题：conda不是内部或者外部命令
  2. 解决办法：手动修改path环境变量，自己添加下图的两个路径
  3. 
• 使用anaconda下载gurobi package
  1. 打开anaconda prompt
  2. 
• 输入指令
  1. conda config --add channels http://conda.anaconda.org/gurobi
  2. conda install gurobi

 

• 测试
• 在gurobi的安装路径下的examples文件夹找一个例子运行
• 也可以直接粘贴我的：

#!/usr/bin/python

# Copyright 2019, Gurobi Optimization, LLC

# Facility location: a company currently ships its product from 5 plants
# to 4 warehouses. It is considering closing some plants to reduce
# costs. What plant(s) should the company close, in order to minimize
# transportation and fixed costs?
#
# Note that this example uses lists instead of dictionaries.  Since
# it does not work with sparse data, lists are a reasonable option.
#
# Based on an example from Frontline Systems:
#   http://www.solver.com/disfacility.htm
# Used with permission.

from gurobipy import *

# Warehouse demand in thousands of units
demand = [15, 18, 14, 20]

# Plant capacity in thousands of units
capacity = [20, 22, 17, 19, 18]

# Fixed costs for each plant
fixedCosts = [12000, 15000, 17000, 13000, 16000]

# Transportation costs per thousand units
transCosts = [[4000, 2000, 3000, 2500, 4500],
              [2500, 2600, 3400, 3000, 4000],
              [1200, 1800, 2600, 4100, 3000],
              [2200, 2600, 3100, 3700, 3200]]

# Range of plants and warehouses
plants = range(len(capacity))
warehouses = range(len(demand))

# Model
m = Model("facility")

# Plant open decision variables: open[p] == 1 if plant p is open.
open = m.addVars(plants,
                 vtype=GRB.BINARY,
                 obj=fixedCosts,
                 name="open")

# Transportation decision variables: transport[w,p] captures the
# optimal quantity to transport to warehouse w from plant p
transport = m.addVars(warehouses, plants, obj=transCosts, name="trans")

# You could use Python looping constructs and m.addVar() to create
# these decision variables instead.  The following would be equivalent
# to the preceding two statements...
#
#open = []
#for p in plants:
#  open.append(m.addVar(vtype=GRB.BINARY,
#                       obj=fixedCosts[p],
#                       name="open[%d]" % p))
#
#transport = []
#for w in warehouses:
#  transport.append([])
#  for p in plants:
#    transport[w].append(m.addVar(obj=transCosts[w][p],
#                                 name="trans[%d,%d]" % (w, p)))

# The objective is to minimize the total fixed and variable costs
m.modelSense = GRB.MINIMIZE

# Production constraints
# Note that the right-hand limit sets the production to zero if the plant
# is closed
m.addConstrs(
    (transport.sum('*',p) <= capacity[p]*open[p] for p in plants),
    "Capacity")

# Using Python looping constructs, the preceding would be...
#
#for p in plants:
#  m.addConstr(sum(transport[w][p] for w in warehouses) <= capacity[p] * open[p],
#              "Capacity[%d]" % p)

# Demand constraints
m.addConstrs(
    (transport.sum(w) == demand[w] for w in warehouses),
    "Demand")

# ... and the preceding would be ...
#for w in warehouses:
#  m.addConstr(sum(transport[w][p] for p in plants) == demand[w], "Demand[%d]" % w)

# Save model
m.write('facilityPY.lp')

# Guess at the starting point: close the plant with the highest fixed costs;
# open all others

# First, open all plants
for p in plants:
    open[p].start = 1.0

# Now close the plant with the highest fixed cost
print('Initial guess:')
maxFixed = max(fixedCosts)
for p in plants:
    if fixedCosts[p] == maxFixed:
        open[p].start = 0.0
        print('Closing plant %s' % p)
        break
print('')

# Use barrier to solve root relaxation
m.Params.method = 2

# Solve
m.optimize()

# Print solution
print('\nTOTAL COSTS: %g' % m.objVal)
print('SOLUTION:')
for p in plants:
    if open[p].x > 0.99:
        print('Plant %s open' % p)
        for w in warehouses:
            if transport[w,p].x > 0:
                print('  Transport %g units to warehouse %s' % \
                      (transport[w,p].x, w))
    else:
        print('Plant %s closed!' % p)

 

1. 1. 发现失败了，没找到gurobipy，检查anaconda
   2. 
   3. 检查file->settings->project interpreter->设置的符号->add
   4. 
   5. 选择anaconda的安装路径下的python
   6. 
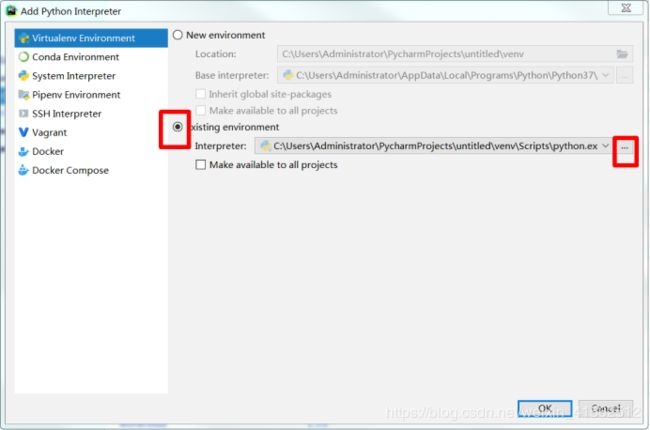
   7. 改完之后图标都会变
   8. 
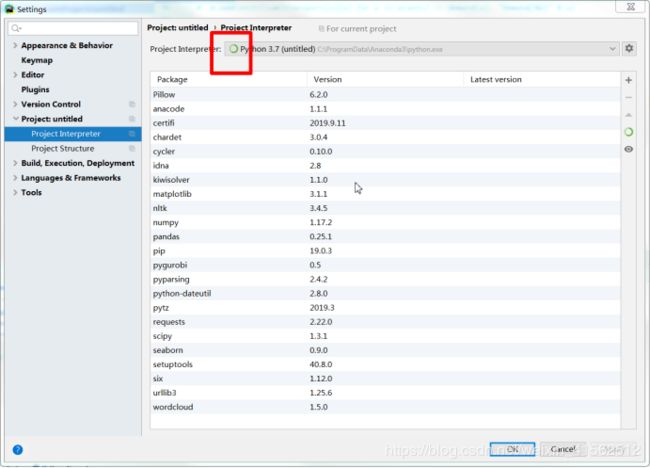
   9. 改完之后会很慢，要等一等
   10. 再次运行，就出结果了，测试成功
   11. 
   12. 错误：
   13. 错误描述：anaconda安装的包在项目中无法使用
   14. 错误原因：可能是自己已经装了python，后装的anaconda，pycharm使用的python路径是自己装的那个版本的，而没使用anaconda中的python
   15. 问题：gurobipy.GurobiError: Version number is 9.0, license is for version 8.0
       1. 解决：使用conda prompt 输入命令：conda install gurobi==8.1.1
       2. 我的gurobi当时使用的就是这个版本，但是最近不小心更新了，导致版本不匹配，改回去就可以