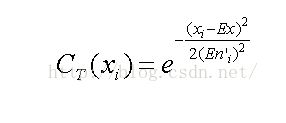产品学习：云模型

一. 云模型研究

        云模型（Cloud model）是我国学者李德毅教授提出的定性和定量转换模型。随着不确定性研究的深入，越来越多的科学家相信，不确定性是这个世界的魅力

所在，只有不确定性本身才是确定的。在众多的不确定性中，随机性和模糊性是最基本的。针对概率论和模糊数学在处理不确定性方面的不足，1995年我国工程院

院士李德毅教授在概率论和模糊数学的基础上提出了云的概念，并研究了模糊性和随机性及两者之间的关联性。自李德毅院士等人提出云模型至今短短的十多年，

其已成功的应用到数据挖掘、决策分析、智能控制等众多领域。 

      船舶运动控制一直以来是控制学领域研究的重点内容，它关系到海洋船舶航行的安全性和经济性。 基于云模型原理，设计一个一维云模型船舶航向控制器。通

过仿真试验希望所提出的控制方法不但能改善系统的动、静态性能,且具有很强的鲁棒性。同时,云模型控制策略简明，无需冗繁的推理计算，通用性强；能够直接

实现定量输入、并行定性推理、定量输出的控制过程，计算量较小，实时性强；易于用软件或者硬件实现其推理过程，具有较好的实际应用价值。

二. 船舶控制理论的发展历史

       船舶航向控制系统最重要的是自动舵，随着控制理论的发展和技术工艺的进步，航向自动舵及其控制算法得到了飞速发展，大致经历了四个发展阶段：

      第一阶段：1922年美国斯佩里公司最先研制出船舶自动操舵仪，即第一代机械式自动舵。尽管但是自动控制理论还尚未形成，已具有经典PID控制规律的雏形

了，它的出现使人们看到了摆脱体力劳动实现自动控制的希望，但它只能用于低精度的航向保持。

      第二阶段：20世纪50年代，出现了集控制技术和电子器件发展成果于一体的第二代自动舵，即PID舵，称为“经典控制理论”时期。经典控制理论是一种单回路

线性控制理论，只适用于单输入单输出的控制系统，主要研究单变量、单系数线性系统，数学模型简单，基本分析和综合方法基于频率法和图解法。经典控制理论

也可以处理简单的非线性控制系统。经典控制理论的研究对象，数学方法和计算手段和当时的社会技术水平和需要密相关。

      第三阶段： 时间为本世纪60 至70 年代，称为“ 现代控制理论”时期。这个时期，由于计算机的飞速发展，推动了空间技术的发展。由此出现了第三代自动舵-自

适应舵。它能自动调节参数，对船舶工作状态和工作环境有一定的适应能力，减轻操作者的负担，提高了船舶操纵的自动化水平，但他是建立在受控对象为线性系

统的基础上，而实际船舶工作状态及航向环境是经常变化的非线性的，所以不可避免的受到鲁棒性等的困扰，影响自适应舵的控制效果。

      第四阶段： 时间为本世纪70 年代末至今。70 年代末，控制理论向着 “智能控制”方向发展，是控制理论在深度上的挖掘，是研究与模拟人类智能活动及其控制

与信息传递过程的规律，研制具有某些仿人智能的工程控制与信息处理系统。因此出现了第四代自动舵-智能式自动舵。这种舵对于过称模型存在的不确定性及干

扰等因素具有良好的鲁棒性，使船舶控制的自适应性和稳定性都有明显的改善和提高，但不足之处是控制器复杂，参数调整相对较难。

三.智能控制的特点

       由于科学技术的高度发展，导致了被控对象结构上的日益复杂化，传统的自动控制理论在面临复杂性所带来的困境时，力图突破旧的模式以适应社会对自动化

学科提出的新要求。人们开始认识到，在许多系统中，复杂性不仅仅表现在高维性上，更多的则是表现在系统信息的模糊性、非线性、不确定性、偶然性和不完全

性上。基于精确模型的理论当然无法解决好它们的控制问题。人工智能的发展促进自动控制向智能控制的方向发展。智能控制是一类无须（或许要尽可能少的）人

的干预就能够独立的驱动智能机器实现其目标的自动控制。许多复杂的系统难以建立有效的数学模型和用常规的控制理论进行定量计算及分析，而必须采用定量数

学分析方法与基于知识的定性方法的混合控制。随着人工智能和计算机技术的发展，把自动控制、人工智能以及系统科学的某些分支结合起来，建立一种适合于复

杂系统的控制理论与控制技术已经成为可能。智能控制正是在这种条件下产生的，它是自动控制的最新发展阶段，也是计算机模拟人类智能的一个重要研究领域。

智能控制是以物理的、定性定量的、结构性的知识模型为基础，对被控过程数学模型的依赖性小，在控制方法上表现出了人的主动性，具有灵活的控制策略和较强

的信息处理能力和适应能力，能解决不确定性问题。正是智能控制的这些特点，才使其得以迅速发展。具体的说，智能控制的研究对象具有以下特点：

①不确定性的模型。这里所说的模型既包括被控对象也包括干扰的模型，此模型不确定性包含两方面的含义：一是模型未知或知之甚少；二是模型的结构参数可能

在很大范围内变化。无论上述哪种情况，用传统的方法都难以进行有效的控制，而这正是智能控制所要解决的问题。

②高度的非线性。在传统的控制理论中，线性系统理论比较成熟，对于具有高度非线性的控制对象，虽然也有一些非线性方法可以利用，但总的来说，非线性理论

还是很不成熟的，而有些方法也过于复杂。智能控制方法可能是解决复杂非线性对象控制问题的一个出路。

③复杂的任务要求。在传统的控制系统中，控制的任务或者是要求输出为定值（调节系统），或者要求输出跟随期望的运动轨迹（跟踪系统），因而控制任务比较

单一。而对智能控制系统，其任务要求比较复杂。对这些复杂问题的要求，仅靠传统的控制方法是难以解决的，采用智能控制方法可以满足复杂的任务要求。

而智能控制系统具有以下特点：

① 定性控制与定量控制的结合。智能控制系统一般具有以知识基非数学广义模型和以数学模型表示的概念控制过程，适用于具有复杂性、不完全性、模糊性、不

确定性以及不存在已知算法的生产过程。因此，在研究和设计智能控制系统时并不把主要的注意力放在对数学公式的表达、计算和处理上，而放在对任务和世界模

型的描述、符号和环境的识别以及知识库和推理机的设计和开发上。也就是说，智能控制系统的设计不在常规的控制器上，而在智能机模型上。

② 具有分层处理和机构。实际上是对人的记忆结构和专家的决策机构的模仿。

③ 智能控制系统具有非线性。作为模仿人的思维进行的控制具有非线性。

④ 具有变结构的特点。在智能控制中，根据当前的偏差和偏差变化率大小和方向，在调整参数时，以跃变形式改变控制器结构以改变控制性能。

⑤ 具有总体寻优特点。智能控制器具有在线特征辨识、在线特征记忆和拟人特点，在整个控制过程中，计算机在线获得和实时处理并给出控制决策，通过不断优

化参数和寻找控制器最佳结构形式、以获得整体最优控制性能。

在自动控制领域内，智能控制是控制技术向智能化发展的成果，它为传统的控制技术带来了新的生机，为解决控制领域的难题，摆脱常规数学模型的困境，突破现

有控制理论的局限，提供了新的途径。

四.云模型的应用

       智能控制与传统控制的主要区别就在于它们处理不确定性和复杂性能力的差异。然而，基于这些智能控制理论所设计的系统往往需要庞大的知识库和相应的推

理机，不利于实时控制。而实时性问题又是控制中的关键问题。这又使智能控制理论发展陷入新的困境。

       要解决这个问题要从两个方面着手，一要研制性能优良的控制方法，二要充分利用人类的智慧，及时地将专家或操作人员的经验知识和直觉推理加到控制决策

中。这就出现了拟人控制系统，拟人控制不要求被控对象的数学模型。但需要强调的是：拟人控制不需要被控对象的数学模型，并不等于对被控对象的先验知识一

无所知的情况下就能设计一个具有良好控制效果的控制器。恰恰相反，它仍要求对被控对象的特性有充分的了解，只不过是它们以知识模型（由人们被控过程认识

的信息归纳和操作经验的总结而形成的模型）而不是数学模型的形式表达出来的。在智能控制领域中，拟人控制占有重要地位。无数事实表明，迄今为止，世界上

最高级最有效的控制系统是人类本身，因此研究人类自身表现出来的控制机制，并用机器加以模拟是智能控制研究十分重要的途径。

       要解决怎样模拟人的控制行为，首先需要研究一下人所具有的控制系统。许多学者曾研究过人控制器的模型，相继提出一些关于人的跟踪系统的连续、离散模

型以及自适应模型等，这些是比较简单的人控制器。然而人的控制系统是一个非常庞大、复杂的系统，而它们的中枢—人脑是我们至今所知道的最复杂的系统，要

从微观结构上完全模仿人脑，就目前的科学技术水平而言，是做不到的。因此，在宏观结构模拟的基础上研究人的控制行为功能并加以模拟实现是目前比较现实的

方法。观察生活中的现象，我们不难发现，人类却能应用定性知识对许多复杂的、难以建立数学模型的系统进行精确地控制。因此控制论如果不突破模型发展就会

始终受限，确切地说模型不能证实只能证明。那么到底用什么方法来描述被控对象？精确数学语言和自然语言是人们普遍使用的两种截然不同的方法。人们最终认

识到只有在特定条件下的最优解，不存在客观条件下的唯一解，不是简单的对与错，常常是一组或几组较好的解。

      把人工智能原理应用在控制系统中，用语言值构成规则，形成一种直观推理的方法。这种拟人控制，不要求给出被控对象精确的数学模型，仅仅依据人的经

验、感觉和逻辑判断，将人用自然语言值定性表达的控制经验，通过语言原子和云模型转换到语言控制规则器中，就能解决非线性问题和不确定性问题。因此，定

性控制作为拟人控制的一种重要的分支，云模型作为定性定量之间有力的转换工具就具有极其重要的应用价值。

五.云定义

       设U是一个定量论域,X∈U,T是与U相关联的定性概念，若U中的元素x(x∈U)对T所表达的定性概念的隶属确定度Ct∈[0,1]是一有稳定倾向的随机数，

则概念T从论域U到区间[0，1]的映射在数域空间的分布，称为云(Cloud)。Ct在[0，1]上取值，云是从论域到区间[0，1]的映射，即：

       Ct:U→[0,1]    (xU)  x→Ct(x)    

此定义还可以推广到多维。

       从云的基本定义可以看出，论域U上的概念T从论域U到区间[0，1]的映射是一对多的关系，既论域中某一元素与它对概念T的隶属度之间的映射是一对多的转

换，而不是传统的模糊隶属函数中的一对一的关系。表达概念T的云有许多云滴组成，每个云滴均是这个定性概念映射到数域空间的一个点，既定性概念的语言值

在数量上的一次具体实现。显然这种实现带有不确定性，模型同时给出这个点能够代表该定性概念的确定程度。云滴的产生是随机的，且每个云滴代表该定性概念

的确定程度也是模糊的，始终存在着细微的变化。某一个云滴的产生对云的整体特征不会产生剧烈的影响，但是，一定数量的云滴的整体分布就体现了云映射的模

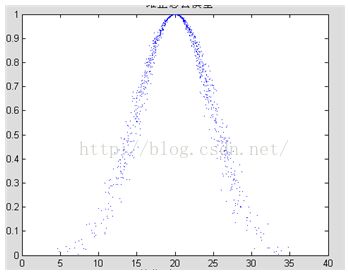
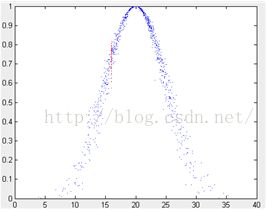
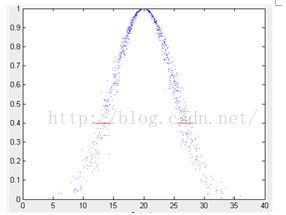
糊性和随机性，即云的整体形状反映了在用定量数值表示定性概念时的不确定性。下面用“青年”这一定性概念给出云模型的例子，如下图示。                          

图1  定性概念“青年”的云模型

六.云的数字特征

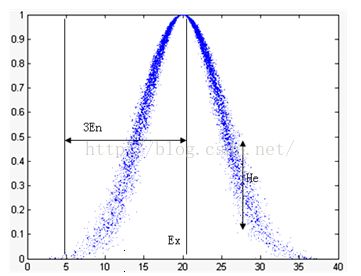
         云的数字特征用期望Ex(Expected Value)、熵En(Entropy)和超熵He(hyper Entropy)来表示，它们反映了定性概念的定量特征。

        期望 Ex：在数域空间中最能够代表这个定性概念的点，反映云的重心位置。

        熵 En：熵作为统计热力学的概念，度量物理系统的无组织度。在云模型中，熵被用来衡量定性概念的模糊度与概率，揭示模糊性与随机性的关联性。熵一  

方面反映了在数域空间中可被语言值接受的范围，即模糊度，是定性概念亦此亦彼性的度量，另一方面还反映了数域空间能够代表这个语言值的概率。表示了云滴

出现的随机性。

       超熵 He：超熵是熵的不确定性的度量，即熵的熵，反映了在数域空间代表该语言值的所有点的不确定度的凝聚性，即云滴的凝聚度。云的数字特征如下图所示。

图2   云模型的数字特征  (Ex,En,He)=(20,5,0.5)

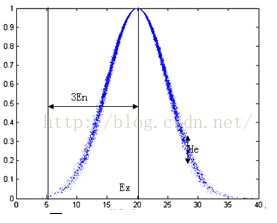
图3 (Ex,En,He)=(20,5,0.2)       

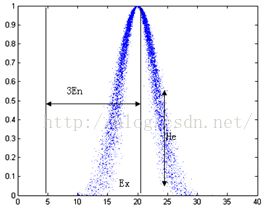
图4    (Ex,En,He)=(20,3,0.5)

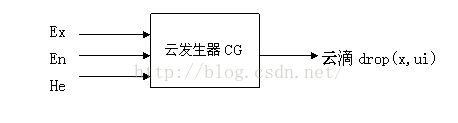
七. 云模型发生器

       云模型发生器（Cloud Ge ner ator，简称CG）指被软件模块化或硬件固化了的云模型的生成算法。云发生器建立起定性和定量之间相互联系、相互依存、性

中有量、量中有性的映射关系，主要包括正向云发生器、逆向云发生器、X 条件云发生器和Y条件云发生器。云发生器是构造不确定性推理的基础，由多个云发生

器按照一定的规律有机地集成一起构成的云模型不确定性推理器，是基于云模型的智能控制器的基本设计工具。由于正态云模型是基本云模型，故主要以正态云模

型为例研究云发生器。

正向云发生器

       正向云发生器（Forward cloud generator）是用语言值描述的某个基本概念与其数值表示之间的不确定性转换模型，是从定性到定量的映射。如图5所示：

图5  正向云发生器

它根据云模型的数字特征产生云滴，积累到一定数量汇聚为云。正向云发生器可以实现从语言值表达的定性信息中获得定量数据的范围和分布规律，是一个前向的、直接的过程，其输入为表示定性概念的期望值Ex 、熵En 和超熵 He，云滴数量N，输出是N 个云滴在数域空间的定量位置及每个云滴代表该概念的确定度。

具体算法为：

输入：（Ex，En，He，N）

输出：(Drop(x1，CT(x1))，Drop (x2，CT(x2))，…，Drop (xN ，CT(xN)))

（1）生成以En为期望值，He为方差的一个正态随机数Eni'= NORM(En，He)

（2）生成以Ex为期望值，Eni'为方差的一个正态随机数xi = NORM(Ex，Eni')

（3）计算：

（4）令带有确定度CT(xi)的xi 成为数域中的一个云滴。

（5）重复步骤（1）~（4），直至产生要求的N 个云滴。

其中，NORM（Ex，Eni'）为生成以Ex 为期望值，Eni'为方差的正态随机数的函数。

给定正态云的三个数字特征值（Ex，En，He），上述算法可以生成任意个云滴组成的正态云模型。上述算法为完整的云形态，半云模型可以在此基础上通过限定所取论域内元素的范围来求得，如左半云为“xi = NORM(Ex，Eni') ，且 xi = 0”。为了说明正向云发生器如何实现精确数据点（云滴）和概念之间的转换。

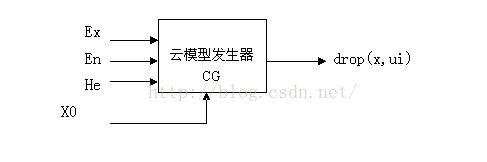
X 条件云发生器

      在给定论域的数域空间中，当已知云的三个数字特征（Ex，En，He）后，如果还有特定的x = x0条件，那么正向云发生器称为X条件云发生器；如果特定的

条件不是x = x0，而是CT(x) = CT(x0)，那么正向云发生器叫做Y条件云发生器或隶属度条件云发生器。由于空间坐标系的纵轴一般称为Y轴，而隶属度CT(x0)又常

常用纵轴表示，因此隶属度条件云发生器更多地被称作Y条件云发生器。X条件云发生器和Y条件云发生器的输出结果都是云带，X条件云发生器为一条，Y条件云发

生器为以云的数学期望为对称中心的对称两条。云带的云滴密集度具有离心衰减的特点，即云带中心对概念的隶属确定度大，云滴密集，越偏离云带中心，对概念

的确定度越小，云滴越稀疏。

       X条件云发生器如图6产生的云滴Drop(x0，CT(xi))都呈概率分布在直线x= x0上，是规则前件表示的基础。其中，CT(xi)是N个隶属度数值的集合，

而不是一个数值。

   

 图6  x条件云发生器结构图

X条件云发生器算法 : 

输入：（Ex，En，He，x0，N）

输出：（Drop(x0，CT(x1))，Drop (x0，CT(x2))，…，Drop (x0，CT(xN))）

（1）：计算Pi＝R1(En，He)。产生一个均值为En，标准差为He的正态分布随机数Pi。

（2）：计算μi＝exp[-0.5(x -Ex)2/ Pi 2]。令数据对(x，μi) 为一维x条件云滴。

（3）：返回step 1，直到产生足够多的一维x条件云滴。

Y条件云发生器

Y条件云发生器(如图7所示)产生的云滴Drop(xi，CT(x0))都呈概率分布在直线CT(x) = CT(x0)上，分别处于期望值Ex 的两侧，被期望值Ex分为左右对称的两部分。Y条件云发生器是规则后件表示的基础。

                                                   

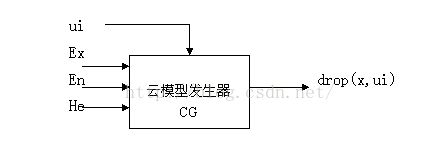
图7 y条件云发生器结构图

Y条件云发生器算法[：

输入：（Ex，En，He，CT(x0)，N）

输出：（Drop(x1，CT(x0))，Drop (x2，CT(x0))，…，Drop (xN，CT(x0))）

（1）：计算Pi＝R1(En，He)。产生一个均值为En，标准差为He的正态分布随机数Pi。

（2）：计算yi ＝Ex±(-2ln(μ))0.5 Pi。如果μ值产生于x条件云的上升沿，则取“-”；否则取“+”。令(yi, μ)为y条件云滴。

（3）：返回step 1，直到产生足够多的y条件云滴。

  

图8  X条件云发生器（图中红色云带）      

 

图9  Y条件云模型

注：横轴为y轴,即输出轴。

从上图中可以看出：x条件云发生器和y条件云发生器的输出结果均为云带。为了更好地理解云带的特性，我们分析一下云带的特征，x条件云发生器产生一条云带，我们将云带的点数设为50，从图中可以看出，云带中云滴的密集度是不同的，具有离心衰减的特点，这里的“心”就是条x0激活的红色云带的中心，云带中心对概念的隶属度的确定度较大，云滴密集，偏离云滴中心越远，对概念的确定度越小，云滴就稀疏。另外，还应指出的是，在x条件云中，每条云带都成概率分布在直线x=x0上，是N个隶属数值的集合，而不是一个数值（图9所示）。在y条件云中，发生器的输出结果应为云滴Drop(yi,Ct(x0))，其中yi的坐标轴为横轴。这样，Y条件云发生器的输出就为两条水平云带，每一条都呈概率分布在直线Ct(x)=Ct(x0)上，云带的特征和x条件云带的特征是相同的。从图中可以看出，y条件云带有两条，左右对称于期望Ex。