算法:堆栈与深度优先搜索(迷宫问题)
堆栈的访问规则被限制为Push和Pop两种操作,Push(入栈或压栈)向栈顶添加元素,Pop(出栈或弹出)则取出当前栈顶的元素,也就是说,只能访问栈顶元素而不能访问栈中其它元素。
现在我们用堆栈解决一个有意思的问题,定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的路线。程序如下:(参考《Linux c 编程一站式学习》)
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
#include typedef struct point { int row, col; } item_t; #define MAX_ROW 5 #define MAX_COL 5 static item_t stack[ 512]; static int top = 0; void push(item_t p) { stack[top++] = p; } item_t pop( void) { return stack[--top]; } int is_empty( void) { return top == 0; } int maze[MAX_ROW][MAX_COL] = { 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; void print_maze( void) { int i, j; for (i = 0; i < MAX_ROW; i++) { for (j = 0; j < MAX_COL; j++) printf( "%d ", maze[i][j]); putchar( '\n'); } printf( "*********\n"); } struct point predecessor[MAX_ROW][MAX_COL] = { {{ - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}}, {{ - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}}, {{ - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}}, {{ - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}}, {{ - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}, { - 1, - 1}}, }; void visit( int row, int col, struct point pre) { struct point visit_point = { row, col }; maze[row][col] = 2; predecessor[row][col] = pre; push(visit_point); } int main( void) { struct point p = { 0, 0 }; maze[p.row][p.col] = 2; push(p); while (!is_empty()) { p = pop(); if (p.row == MAX_ROW - 1 /* goal */ && p.col == MAX_COL - 1) break; if (p.col + 1 < MAX_COL /* right */ && maze[p.row][p.col + 1] == 0) visit(p.row, p.col + 1, p); if (p.row + 1 < MAX_ROW /* down */ && maze[p.row + 1][p.col] == 0) visit(p.row + 1, p.col, p); if (p.col - 1 >= 0 /* left */ && maze[p.row][p.col - 1] == 0) visit(p.row, p.col - 1, p); if (p.row - 1 >= 0 /* up */ && maze[p.row - 1][p.col] == 0) visit(p.row - 1, p.col, p); print_maze(); } if (p.row == MAX_ROW - 1 && p.col == MAX_COL - 1) { printf( "(%d, %d)\n", p.row, p.col); while (predecessor[p.row][p.col].row != - 1) { p = predecessor[p.row][p.col]; printf( "(%d, %d)\n", p.row, p.col); } } else printf( "No path!\n"); return 0; } |
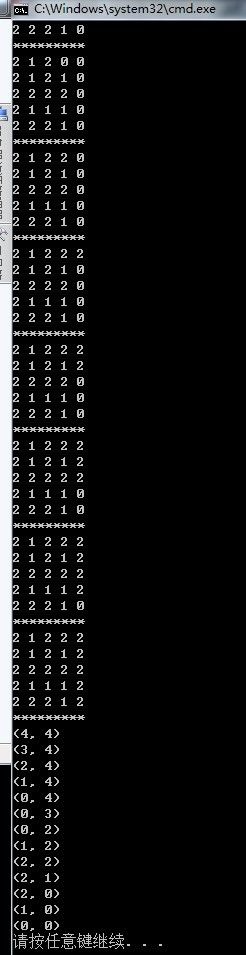
输出为:
这次堆栈里的元素是结构体类型的,用来表示迷宫中一个点的x和y坐标。我们用一个新的数据结构保存走迷宫的路线,每个走过的点都有一个前趋(Predecessor)点,表示是从哪儿走到当前点的,比如predecessor[4][4]是坐标为(3, 4)的点,就表示从(3, 4)走到了(4, 4),一开始predecessor的各元素初始化为无效坐标(-1, -1)。在迷宫中探索路线的同时就把路线保存在predecessor数组中,已经走过的点在maze数组中记为2防止重复走,最后找到终点时就根据predecessor数组保存的路线从终点打印到起点。为了帮助理解,把这个算法改写成伪代码(Pseudocode)如下图:
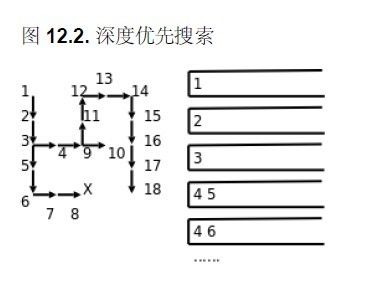
程序在while循环的末尾插了打印语句,每探索一步都打印出当前迷宫的状态(标记了哪些点),从打印结果可以看出这种搜索算法的特点是:每次探索完各个方向相邻的点之后,取其中一个相邻的点走下去,一直走到无路可走了再退回来,取另一个相邻的点再走下去。这称为深度优先搜索(DFS,Depth First Search)。探索迷宫和堆栈变化的过程如下图所示。
图中各点的编号表示探索顺序,堆栈中保存的应该是坐标,在画图时为了直观就把各点的编号写在堆栈里了。可见正是堆栈后进先出的性质使这个算法具有了深度优先的特点。如果在探索问题的解时走进了死胡同,则需要退回来从另一条路继续探索,这种思想称为回溯(Backtrack),一个典型的例子是很多编程书上都会讲的八皇后问题。
最后我们打印终点的坐标并通过predecessor数据结构找到它的前趋,这样顺藤摸瓜一直打印到起点。那么能不能从起点到终点正向打印路线呢?,数组支持随机访问也支持顺序访问,如果在一个循环里打印数组,既可以正向打印也可以反向打印。但predecessor这种数据结构却有很多限制:
1. 不能随机访问一条路线上的任意点,只能通过一个点找到另一个点,通过另一个点再找第三个点,因此只能顺序访问。
2. 每个点只知道它的前趋是谁,而不知道它的后继(Successor)是谁,所以只能反向顺序访问。
可见,有什么样的数据结构就决定了可以用什么样的算法。那为什么不再建一个successor数组来保存每个点的后继呢?从DFS算法的过程可以看出,虽然每个点的前趋只有一个,后继却不止一个,如果我们为每个点只保存一个后继,则无法保证这个后继指向正确的路线。由此可见,有什么样的算法就决定了可以用什么样的数据结构。设计算法和设计数据结构这两件工作是紧密联系的。
参考:《Linux c 编程一站式学习》