数组、矩阵类算法题
一.移动零
力扣传送门
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作,不能拷贝额外的数组。
尽量减少操作次数。
/*
* 把数组中的 0 移到末尾
* */
public void moveZeroes(int[] nums) {
if (nums == null || nums.length == 0) return;
int n = nums.length;
int curIndex = 0;
for (int i = 0; i < n; i++) {
if (nums[i] != 0) nums[curIndex++] = nums[i];
}
while (curIndex < n) {
nums[curIndex++] = 0;
}
return;
}
二.改变矩阵维度
力扣传送门
在MATLAB中,有一个非常有用的函数 reshape,它可以将一个矩阵重塑为另一个大小不同的新矩阵,但保留其原始数据。
给出一个由二维数组表示的矩阵,以及两个正整数r和c,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。
如果具有给定参数的reshape操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
/*
* 重塑矩阵
* */
public int[][] matrixReshape(int[][] nums, int r, int c) {
if (nums == null || nums.length == 0) return null;
int n = nums.length;
int m = nums[0].length;
if (n * m != r * c) return null;
int newNums[][] = new int[r][c];
int row = 0, col = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (col == c) {
row++;
col = 0;
}
newNums[row++][col++] = nums[i][j];
}
}
return newNums;
}
三.找出数组中最长的连续 1
力扣传送门
/*
* 找出数组中最长的连续 1
* 给定一个二进制数组, 计算其中最大连续1的个数。
* */
public int findMaxConsecutiveOnes(int[] nums) {
int curlen = 0;
int maxlen = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 1) curlen++;
else curlen = 0;
maxlen = Math.max(maxlen, curlen);
}
return maxlen;
}
四.有序矩阵查找
力扣传送门
/*
* 有序矩阵查找
* */
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0) return false;
int m = matrix.length;
int n = matrix[0].length;
int row = 0;
int col = n - 1;
while (row < m && col >= 0) {
if (matrix[row][col] == target) {
return true;
} else if (matrix[row][col] > target) {
col--;
} else {
row++;
}
}
return false;
}
五.一个数组元素在 [1, n] 之间,其中一个数被替换为另一个数,找出重复的数和丢失的数
力扣传送门
public int[] findErrorNums(int[] nums) {
if (nums == null || nums.length == 0) return null;
int n = nums.length;
int result[] = new int[2];
for (int i = 0; i < n; ) {
if (i != nums[i] - 1) {
if (nums[nums[i] - 1] == nums[i]) {
result[0] = nums[i];
i++;
} else {
swap(nums, i, nums[i] - 1);
}
} else {
i++;
}
}
for (int i = 0; i < n; i++) {
if (nums[i] - 1 != i) {
result[1] = i + 1;
break;
}
}
return result;
}
六.优美的排列 II —数组相邻差值的个数
题目描述:数组元素为 1~n 的整数,要求构建数组,使得相邻元素的差值不相同的个数为 k。
力扣传送门
解法一:dfs超时
public int[] constructArray(int n, int k) {//方法一:dfs超时
boolean book[] = new boolean[n + 1];
int result[] = new int[n];
HashSet set = new HashSet<>();
dfs(book, result, 0, set, n, k);
return res;
}
int res[] = null;
public void dfs(boolean book[], int result[], int curIndex, HashSet set, int n, int k) {
if (curIndex == n && set.size() == k) {
res = new int[n];
for (int i = 0; i < n; i++) {
res[i] = result[i];
}
return;
}
if (curIndex > n || set.size() > k) return;//剪枝
for (int i = 1; i <= n; i++) {
if (book[i]) continue;
book[i] = true;
result[curIndex] = i;
if (curIndex > 0) set.add(Math.abs(result[curIndex - 1] - i));
dfs(book, result, curIndex + 1, set, n, k);
if (curIndex > 0) set.remove(Math.abs(result[curIndex - 1] - i));
book[i] = false;
}
}
解法二:不断反转
若n=8初始状态
1 2 3 4 5 6 7 8
k=1------ | 1 2 3 4 5 6 7 8 (不翻转,直接返回)
k=2------ 1 | 8 7 6 5 4 3 2
k=3------ 1 8 | 2 3 4 5 6 7
k=4------ 1 8 2 | 7 6 5 4 3
public int[] constructArray2(int n, int k) {//方法二:不断反转
int a[] = new int[n];
for (int i = 0; i < n; i++) a[i] = i + 1;
int cur = 1;
for (int j = 0; j < k - 1; j++) {
reverse(a, cur, n - 1);
cur++;
}
return a;
}
public void reverse(int a[], int start, int end) {
while (start < end) {
int tmp = a[start];
a[start] = a[end];
a[end] = tmp;
start++;
end--;
}
}
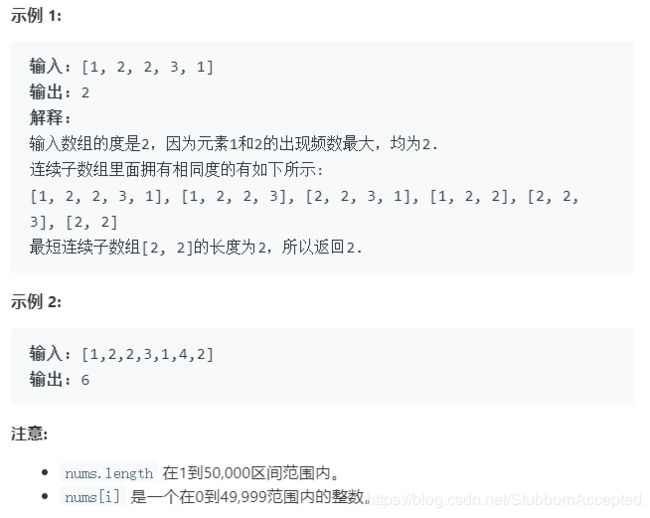
七.数组的度
力扣传送门
给定一个非空且只包含非负数的整数数组 nums, 数组的度的定义是指数组里任一元素出现频数的最大值。
你的任务是找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
解法一:
public int findShortestSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int num = -1;//保存目前为止出现最高频率的数字
int maxCount = 0;//保存目前为止的最高频率
int minlen = 1;//保存最高频率数字的长度
Map map = new HashMap<>();//保存数字的频率
Map mapStart = new HashMap<>();//保存数字的开始位置
for (int i = 0; i < nums.length; i++) {
if (!mapStart.containsKey(nums[i])) {//不包含 put
mapStart.put(nums[i], i);
map.put(nums[i], 0);
} else {//包含 计数
map.put(nums[i], map.get(nums[i]) + 1);
}
int count = map.get(nums[i]);
if (count > maxCount) {//当前数字的频率大于最高频率
num = nums[i];//更新最高频率数字
maxCount = count;//更新频率
minlen = i - mapStart.get(nums[i]) + 1;//更新最高频率数字长度
}
if (count == maxCount) {//当前数字的频率等于最高频率
int curlen = i - mapStart.get(nums[i]) + 1;
if (curlen < minlen) {//比较长度,取短的
num = nums[i];
maxCount = count;
minlen = curlen;
}
}
}
return minlen;
}
解法二:
public int findShortestSubArray2(int[] nums) {
Map leftmap = new HashMap<>();
Map rightmap = new HashMap<>();
Map countmap = new HashMap<>();
int maxCount = 0;
for (int i = 0; i < nums.length; i++) {
if (!leftmap.containsKey(nums[i])) {
leftmap.put(nums[i], i);
}
rightmap.put(nums[i], i);
int curCount = countmap.getOrDefault(nums[i], 0) + 1;
maxCount = Math.max(maxCount, curCount);
countmap.put(nums[i], curCount);
}
int minlen = nums.length;
Iterator> iterator = countmap.entrySet().iterator();//注意map遍历方式
while (iterator.hasNext()) {
Map.Entry entry = iterator.next();
if (entry.getValue() == maxCount) {
minlen = Math.min(minlen, rightmap.get(entry.getKey()) - leftmap.get(entry.getKey()) + 1);
}
}
return minlen;
}
八.对角元素相等的矩阵
力扣传送门
如果一个矩阵的每一方向由左上到右下的对角线上具有相同元素,那么这个矩阵是托普利茨矩阵。
给定一个 M x N 的矩阵,当且仅当它是托普利茨矩阵时返回 True。

解法一:
/*
* 对角元素相等的矩阵
* */
public boolean isToeplitzMatrix(int[][] matrix) {
int n = matrix.length;
int m = matrix[0].length;
for (int i = 0; i < n; i++) {
int x = i, y = 0;
int num = matrix[i][0];
while (x < n && y < m) {
if (matrix[x][y] != num) return false;
x++;
y++;
}
}
for (int j = 0; j < m; j++) {
int x = 0, y = j;
int num = matrix[0][j];
while (x < n && y < m) {
if (matrix[x][y] != num) return false;
x++;
y++;
}
}
return true;
}
解法二:
class Solution {
public boolean isToeplitzMatrix(int[][] matrix) {
Map groups = new HashMap();
for (int r = 0; r < matrix.length; ++r) {
for (int c = 0; c < matrix[0].length; ++c) {
if (!groups.containsKey(r-c))
groups.put(r-c, matrix[r][c]);
else if (groups.get(r-c) != matrix[r][c])
return False;
}
}
return True;
}
}
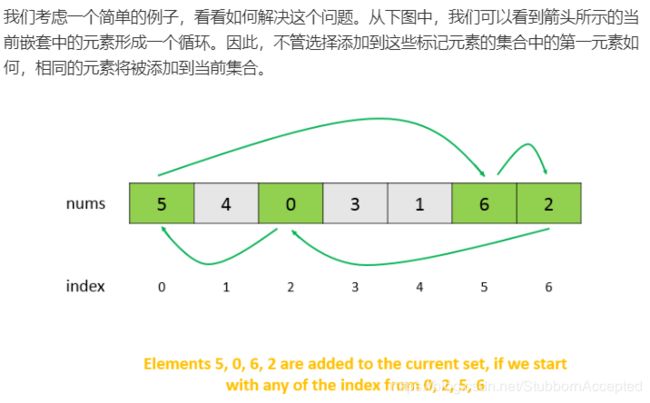
九.嵌套数组
力扣传送门
索引从0开始长度为N的数组A,包含0到N - 1的所有整数。找到并返回最大的集合S,S[i] = {A[i], A[A[i]], A[A[A[i]]], … }且遵守以下的规则。
假设选择索引为i的元素A[i]为S的第一个元素,S的下一个元素应该是A[A[i]],之后是A[A[A[i]]]… 以此类推,不断添加直到S出现重复的元素。
public int arrayNesting(int[] nums) {
int n = nums.length;
boolean book[] = new boolean[n];
int maxLen = 0;
for (int i = 0; i < n; i++) {
int tmp = i;
int count = 0;
while (!book[tmp]) {
count++;
book[tmp] = true;
tmp = nums[tmp];
}
maxLen = Math.max(maxLen, count);
}
return maxLen;
}
十.最多能完成排序的块—分割数组
力扣传送门
数组arr是[0, 1, …, arr.length - 1]的一种排列,我们将这个数组分割成几个“块”,并将这些块分别进行排序。之后再连接起来,使得连接的结果和按升序排序后的原数组相同。
/*
* 分割数组
* 分隔数组,使得对每部分排序后数组就为有序。
* */
public int maxChunksToSorted(int[] arr) {//做法一
int n = arr.length;
boolean book[] = new boolean[n];
HashMap map = new HashMap<>();
int count = 0;
int pre = 0;
for (int i = 0; i < arr.length; i++) {
book[arr[i]] = true;
boolean flag = true;
for (int j = pre; j <= i; j++) {//每遍历一个arr[i]就判断,在i位置之前的元素是否都已出现过
if (!book[j]) flag = false;
}
if (flag) {
pre = i + 1;
count++;
}
}
return count;
}
public int maxChunksToSorted2(int[] arr) {//做法二
int n = arr.length;
int right = -1;//标记最右位置
int count = 0;
for (int i = 0; i < n; i++) {
right = Math.max(right, arr[i]);
if (right == i) count++;
}
return count;
}