线性结构的两种应用：栈与队列

一 栈

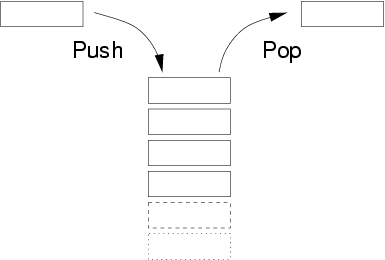
① 什么是栈：一种可以实现先进后出的数据结构。

 

栈类似于一个箱子，先放进去的书，最后才能取出来，同理，后放进去的书，先取出来

 

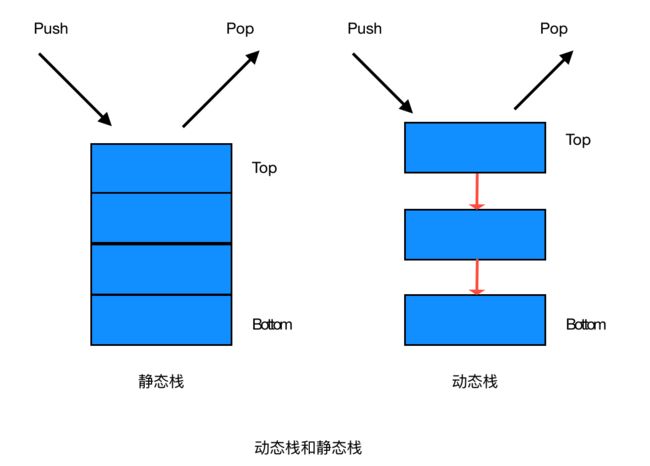
② 栈的分类：静态栈和动态栈

 

静态栈：

　　静态栈的核心是数组，类似于一个连续内存的数组，我们只能操作其栈顶元素。

动态栈：

　　动态栈的核心是链表。

 

 ③ 栈的算法：

栈的算法主要是压栈和出栈两种操作：

那么对于栈的操作，我们应该知道：

　　1、栈操作的对象是一个一个的节点。

　　2、栈本身也是一种存储的数据结构。

　　3、栈有  初始化、压栈、出栈、判空、遍历、清空等主要方法

class Stack(object):
    def __init__(self):
        self.pTop = None
        self.pBottom = None
class Node(object):
    def __init__(self, data=None, pNext = None):
        self.data = data
        self.pNext = pNext
def push(s, new):
    new.pNext = s.pTop
    s.pTop = new
def pop(s):
    cur = s.pTop
    # while cur != s.pBottom:
    #     if cur.data == val:
    #         s.pTop = cur.pNext
    #         break
    #     cur = cur.pNext
    # else:
    #     print('没有找到此元素')
    while cur != s.pBottom:
        s.pTop = cur.pNext
        print("出栈的元素是: %d" % cur.data)
        cur = cur.pNext
    else:
        print("出栈失败")
def getAll(s):
    cur = s.pTop
    while cur != s.pBottom:
        print(cur.data)
        cur = cur.pNext
def is_empty(s):
    if s.pTop == s.pBottom:
        return True
    else:
        return False
def clear(s):
    if is_empty(s):
        return None
    p = s.pTop
    q = None
    while p != s.pBottom:
        q = p.pNext
        del p
        p = q
    else:
        s.pBottom = s.pTop
head = Node()
s = Stack()
s.pTop = s.pBottom = head
n1 = Node(2)
push(s, n1)
n1 = Node(5)
push(s, n1)
n1 = Node(89)
push(s, n1)
print("##############遍历元素##########")
getAll(s)
# print("##############出栈元素#######")
# pop(s)
print("##############清空栈##########")
clear(s)
print("##############遍历元素##########")
getAll(s)

栈的操作

 

④ 栈的应用：

• 函数调用：先调用的函数后返回，栈顶的函数永远先执行。
• 中断
• 表达式求值
• 内存分配
• 走迷宫

 

二 队列

什么叫队列：一种可以实现先进先出的数据结构。

 

队列分类：

　　静态队列

　　链式队列（动态队列）

 

class Node:
    def __init__(self, value):
        self.data = value
        self.next = None
class Queue:
    def __init__(self):
        self.front = Node(None)
        self.rear = self.front
    def enQueue(self, element):
        n = Node(element)
        self.rear.next = n
        self.rear = n
    def deQueue(self):
        if self.empty():
            print('队空')
            return
        temp = self.front.next
        self.front = self.front.next
        if self.rear == temp:
            self.rear = self.front
        del temp
    def getHead(self):
        if self.empty():
            print('队空')
            return
        return self.front.next.data
    def empty(self):
        return self.rear == self.front
    def printQueue(self):
        cur = self.front.next
        while cur != None:
            print(cur.data)
            cur = cur.next
    def length(self):
        cur = self.front.next
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count
if __name__ == '__main__':
    queue = Queue()
    queue.enQueue(23)
    queue.enQueue(2)
    queue.enQueue(4)
    queue.printQueue()
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)

链式队列的算法

实际应用：

所有和时间有关的操作都和队列有关

递归定义：

一个函数自己或者间接调用自己

多个函数调用：

当有多个函数调用时，按照“先调用后返回”的原则，函数之间的信息传递和控制转移必须借助栈来实现，即系统将整个程序运行时所需要的数据空间安排在一个栈中，每当调用一个函数时，就在栈顶分配一个存储区，进行压栈操作，每当一个函数退出时，就释放他的存储区，即进行出栈操作，当前运行的函数永远在栈顶的位置

def f():
print('FFFFFFF')
g()
print('111111')
 
def g():
print('GGGGGGG')
k()
print('222222')
 
def k():
print('KKKKKKK')
 
if __name__ == "__main__":
f()

 

递归满足的条件自己调用自己也是和上面的原理一样：

def f(n):
if n == 1:
print('hello')
else:
f(n-1)

 

• 递归必须有一个明确的终止条件
• 该函数所处理的数据规模是必须递减的
• 这个转化必须是可解的

求阶乘

n规模的实现，得益于n-1规模的实现

# for循环实现

multi = 1

for i in range(3):
multi = multi * (i+1)
print(multi)
 
# 递归实现
 
def f(n):
if 1 == n:
return 1
else:
return f(n-1)*n

 

1+2+3…+100的和

def sum(n):
if 1 == n:
return n
else:
return sum(n-1) + n

 

递归和循环的区别

• 递归
  • 不易于理解
  • 速度慢
  • 存储空间大
• 循环
  • 易于理解
  • 速度快
  • 存储空间小

递归的应用

树和森林就是以递归的方式定义的
树和图的算范就是以递归的方式实现的
很多数学公式就是以递归的方式实现的（斐波那楔序列）

 

阶段总结

数据结构：
从狭义的方面讲：

• 数据结构就是为了研究数据的存储问题
• 数据结构的存储包含两个方面：个体的存储 + 个体关系的存储

从广义方面来讲：

• 数据结构既包含对数据的存储，也包含对数据的操作
• 对存储数据的操作就是算法

算法
从狭义的方面讲：

• 算法是和数据的存储方式有关的

从广义的方面讲：

• 算法是和数据的存储方式无关，这就是泛型的思想

非线性结构

树

树的定义

我们可以简单的认为：

• 树有且仅有一个根节点
• 有若干个互不相交的子树，这些子树本身也是一颗树

通俗的定义：
1.树就是由节点和边组成的
2.每一个节点只能有一个父节点，但可以有多个子节点。但有一个节点例外，该节点没有父节点，此节点就称为根节点

树的专业术语

• 节点
• 父节点
• 子节点
• 子孙
• 堂兄弟
• 兄弟
• 深度
  • 从根节点到最底层节点的层数被称为深度，根节点是第一层
• 叶子节点
  • 没有子节点的节点
• 度
  • 子节点的个数

树的分类

• • 一般树
    • 任意一个节点的子节点的个数不受限制
  • 二叉树
    • 定义：任意一个节点的子节点的个数最多是两个，且子节点的位置不可更改
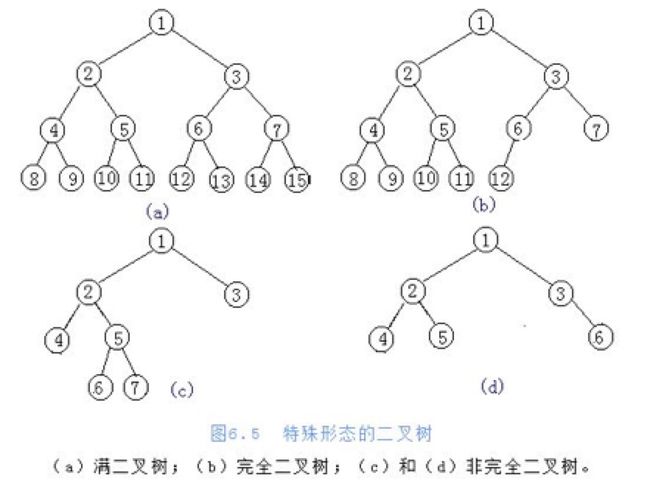
      • 满二叉树
        • 定义：在不增加层数的前提下，无法再多添加一个节点的二叉树
      • 完全二叉树
        • 定义：只是删除了满二叉树最底层最右边连续的若干个节点
      • 一般二叉树

 

 

树的操作（伪算法)

 

如何把一个非线性结构的数据转换成一个线性结构的数据存储起来？

• 一般树的存储
  • 双亲表示法
    • 求父节点方便
  • 孩子表示法
    • 求子节点方便
  • 双亲孩子表示法
    • 求父节点和子节点都很方便
  • 二叉树表示法
    • 即把一般树转换成二叉树，按照二叉树的方式进行存储
    • 具体的转化办法：
      • 设法保证任意一个节点的：
        • 左指针域指向它的第一个孩子
        • 右指针域指向它的下一个兄弟
      • 只要能满足上述的条件就能够转化成功

• 二叉树的操作

  • 连续存储 （完全二叉树，数组方式进行存储）
    • 优点：查找某个节点的父节点和子节点非常的快
    • 缺点：耗用内存空间过大
    • 转化的方法：先序 中序 后序
  • 链式存储 （链表存储）
    • data区域 左孩子区域 右孩子区域

• 森林的操作

  • 把所有的树转化成二叉树，方法同一般树的转化

二叉树具体的操作

1.二叉树的先序遍历[先访问根节点]

• 先访问根节点
• 再先序遍历左子树
• 再先序遍历右子树

2.二叉树的中序遍历 [中间访问根节点]

• 先中序遍历左子树
• 再访问根节点
• 再中序遍历右子树

3.二叉树的后序遍历 [最后访问根节点]

• 先中序遍历左子树
• 再中序遍历右子树
• 再访问根节点

4.已知先序和中序，如何求出后序？

#### 例一
先序：ABCDEFGH
中序：BDCEAFHG
 
求后序？
后序：DECBHGFA
 
#### 例二
先序：ABDGHCEFI
中序：GDHBAECIF
 
求后序？
后序：GHDBEIFCA

 

树的应用

中序：BDCEAFHG
后序：DECBHGFA
 
求先序？
先序：ABCDEFGH

 

5.已知中序和后序，如何求出先序？

• 树是数据库中数据组织的一种重要形式
• 操作系统子父进程的关系本身就是一颗树
• 面型对象语言中类的继承关系

总结

数据结构研究的就是数据的存储和数据的操作的一门学问

数据的存储又分为两个部分：

• 个体的存储
• 个体关系的存储

从某个角度而言，数据存储最核心的就是个体关系如何进行存储
个体的存储可以忽略不计

 

转载于:https://www.cnblogs.com/zhangsanfeng/p/9587749.html