第八届蓝桥杯大赛省赛-C语言B组

等差素数列

2,3,5,7,11,13,…是素数序列。
类似：7,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。
上边的数列公差为30，长度为6。
2004年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。
这是数论领域一项惊人的成果！
有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：
长度为10的等差素数列，其公差最小值是多少？
注意：需要提交的是一个整数，不要填写任何多余的内容和说明文字。

思路：将所有的素数找出来，暴力枚举。

#include 
#include 
using namespace std;
const int M=1e5+10;
int a[M];
void init()
{
    int i,j;
    memset(a,0,sizeof(a));
    for(i=2; i<100000; i++)
    {
        if(a[i]==0)
        {
            for(j=i+i; j<100000; j+=i)
                a[j]=1;
        }
    }
}
int main()
{
    init();
    int i,j,k;
    for(i=2; i<500; i++)
    {
        if(a[i]==0)
        {
            for(j=1; j<500; j++)
            {
            int d=i;
                for(k=0; k<10; k++)
                {
                    if(a[d])
                        break;
                    d+=j;
                }
                if(k==10)
                {
                    cout<<"开始"<<i<<"公差"<<j<<endl;
                    return 0;
                }

            }
        }
    }
    return 0;
}

承压计算

X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。

每块金属原料的外形、尺寸完全一致，但重量不同。
金属材料被严格地堆放成金字塔形。

                         7 
                        5 8 
                       7 8 8 
                      9 2 7 2 
                     8 1 4 9 1 
                    8 1 8 8 4 1 
                   7 9 6 1 4 5 4 
                  5 6 5 5 6 9 5 6 
                 5 5 4 7 9 3 5 5 1 
                7 5 7 9 7 4 7 3 3 1 
               4 6 4 5 5 8 8 3 2 4 3 
              1 1 3 3 1 6 6 5 5 4 4 2 
             9 9 9 2 1 9 1 9 2 9 5 7 9 
            4 3 3 7 7 9 3 6 1 3 8 8 3 7 
           3 6 8 1 5 3 9 5 8 3 8 1 8 3 3 
          8 3 2 3 3 5 5 8 5 4 2 8 6 7 6 9 
         8 1 8 1 8 4 6 2 2 1 7 9 4 2 3 3 4 
        2 8 4 2 2 9 9 2 8 3 4 9 6 3 9 4 6 9 
       7 9 7 4 9 7 6 6 2 8 9 4 1 8 1 7 2 1 6 
      9 2 8 6 4 2 7 9 5 4 1 2 5 1 7 3 9 8 3 3 
     5 2 1 6 7 9 3 2 8 9 5 5 6 6 6 2 1 8 7 9 9 
    6 7 1 8 8 7 5 3 6 5 4 7 3 4 6 7 8 1 3 2 7 4 
   2 2 6 3 5 3 4 9 2 4 5 7 6 6 3 2 7 2 4 8 5 5 4 
  7 4 4 5 8 3 3 8 1 8 6 3 2 1 6 2 6 4 6 3 8 2 9 6 
 1 2 4 1 3 3 5 3 4 9 6 3 8 6 5 9 1 5 3 2 6 8 8 5 3 
2 2 7 9 3 3 2 8 6 9 8 4 4 9 5 8 2 6 3 4 8 4 9 3 8 8 

7 7 7 9 7 5 2 7 9 2 5 1 9 2 6 5 3 9 3 5 7 3 5 4 2 8 9
7 7 6 6 8 7 5 5 8 2 4 7 7 4 7 2 6 9 2 1 8 2 9 8 5 7 3 6
5 9 4 5 5 7 5 5 6 3 5 3 9 5 8 9 5 4 1 2 6 1 4 3 5 3 2 4 1
X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X

其中的数字代表金属块的重量（计量单位较大）。
最下一层的X代表30台极高精度的电子秤。
假设每块原料的重量都十分精确地平均落在下方的两个金属块上，
最后，所有的金属块的重量都严格精确地平分落在最底层的电子秤上。
电子秤的计量单位很小，所以显示的数字很大。
工作人员发现，其中读数最小的电子秤的示数为：2086458231
请你推算出：读数最大的电子秤的示数为多少？
注意：需要提交的是一个整数，不要填写任何多余的内容。

#include 
#include 
#include 
#include 
using namespace std;

int main()
{
    double a[40][40];
    memset(a,0,sizeof(a));
    int i,j;
    for(i=1; i<=29; i++)
        for(j=1; j<=i; j++)
            cin>>a[i][j];
    for(i=1; i<=29; i++)
    {
        for(j=1; j<=i; j++)
        {
            a[i+1][j]+=a[i][j]/2;
            a[i+1][j+1]+=a[i][j]/2;
            cout<<a[i][j]<<' ';
        }
        cout<<endl;
    }
    sort(a[30]+1,a[30]+31);
    cout<<a[30][1]<<" "<<a[30][30]<<endl;
    cout<<a[30][30]*2086458231/a[30][1]<<endl;
    printf("%lf\n",a[30][30]*2086458231/a[30][1]);
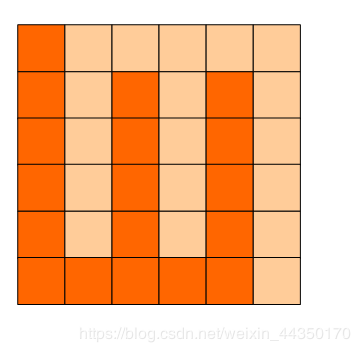
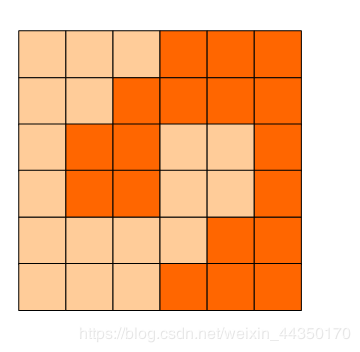
    return 0;
}

方格分割

6x6的方格，沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。

如图：p1.png, p2.png, p3.png 就是可行的分割法。

试计算：
包括这3种分法在内，一共有多少种不同的分割方法。
注意：旋转对称的属于同一种分割法。

请提交该整数，不要填写任何多余的内容或说明文字。

#include 
#include 
#include 
#define mem(a,b) memset(a,b,sizeof(a));
using namespace std;
int mp[7][7];
int re=0;
int d[][4]={{1,-1,0,0},{0,0,1,-1}};
void dfs(int x,int y)
{
    int i;
    if(x==0||x==6||y==0||y==6)
    {
        re++;
        return;
    }
    for(i=0;i<4;i++)
    {
        int dx=x+d[0][i];
        int dy=y+d[1][i];
        if(mp[dx][dy]==0&&mp[6-dx][6-dy]==0)
        {
            mp[dx][dy]=1;
            mp[6-dx][6-dy]=1;
            dfs(dx,dy);
            mp[dx][dy]=0;
            mp[6-dx][6-dy]=0;
        }
    }
}
int main()
{
    mem(mp,0);
    mp[3][3]=1;
    dfs(3,3);
    cout<<re/4<<endl;
    return 0;
}

取数位

题意：取一个数的第k位。

#include 
#include 
#include 
using namespace std;

int len(int x){
	if(x<10) return 1;
	return len(x/10)+1;
}
int f(int x, int k){
	if(len(x)-k==0) return x%10;
	return f(x/10,3);
}

int main()
{
	int x = 23574;
	printf("%d\n", f(x,3));
	return 0;
}

最大公共子串

题意：最长公共子序列。

#include 
#include 
#include 
#include 
#define N 256
using namespace std;

int f(const char* s1, const char* s2)
{
	int a[N][N];
	int len1 = strlen(s1);
	int len2 = strlen(s2);
	int i,j;

	memset(a,0,sizeof(int)*N*N);
	int maxn = 0;
	for(i=1; i<=len1; i++){
		for(j=1; j<=len2; j++){
			if(s1[i-1]==s2[j-1]) {
				a[i][j] = max(max(a[i-1][j],a[i][j-1]),a[i-1][j-1]+1);
				if(a[i][j] > maxn) maxn = a[i][j];
			}
		}
	}

	return maxn;
}

int main()
{
	printf("%d\n", f("abcdkkk", "baabcdadabc"));
	return 0;
}

日期问题

小明正在整理一批历史文献。这些历史文献中出现了很多日期。小明知道这些日期都在1960年1月1日至2059年12月31日。令小明头疼的是，这些日期采用的格式非常不统一，有采用年/月/日的，有采用月/日/年的，还有采用日/月/年的。更加麻烦的是，年份也都省略了前两位，使得文献上的一个日期，存在很多可能的日期与其对应。

比如02/03/04，可能是2002年03月04日、2004年02月03日或2004年03月02日。
给出一个文献上的日期，你能帮助小明判断有哪些可能的日期对其对应吗？

输入

一个日期，格式是"AA/BB/CC"。  (0 <= A, B, C <= 9)  

输入

输出若干个不相同的日期，每个日期一行，格式是"yyyy-MM-dd"。多个日期按从早到晚排列。  

样例输入

02/03/04  

样例输出

2002-03-04  
2004-02-03  
2004-03-02  

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

#include 
#include 
#include 
#include 
#include 
using namespace std;
int monthday1[12] = { 31,28,31,30,31,30,31,31,30,31,30,31 };
int monthday2[12] = { 31,29,31,30,31,30,31,31,30,31,30,31 };
int e=0;
struct rq
{
    int year,b,c;
};
rq r[20];
bool cmp(rq n,rq m)
{
    if(n.year!=m.year)
        return n.year<m.year;
    else if(n.year==m.year&&n.b!=m.b)
        return n.b<m.b;
    else if(n.year==m.year&&n.b==m.b)
        return n.c<m.c;
}
void fun(int a,int b,int c)
{
    int year;
    year=1900+a;
    if(year>=1960&&year<=2059)
    {
        if (year % 400 == 0 || (year % 4 == 0 && (year % 100 != 0)))
        {
            if(b>=1&&b<=12)
            {
                if(c>=1&&c<=monthday2[b])
                {
                    r[e].year=year;
                    r[e].b=b;
                    r[e].c=c;
                    e++;
                }

            }
        }
        else
        {
            if(b>=1&&b<=12)
            {
                if(c>=1&&c<=monthday1[b])
                {
                    r[e].year=year;
                    r[e].b=b;
                    r[e].c=c;
                    e++;
                }

            }
        }
    }
    year=2000+a;
    if(year>=1960&&year<=2059)
    {
        if (year % 400 == 0 || (year % 4 == 0 && (year % 100 != 0)))
        {
            if(b>=1&&b<=12)
            {
                if(c>=1&&c<=monthday2[b])
                {
                    r[e].year=year;
                    r[e].b=b;
                    r[e].c=c;
                    e++;
                }

            }
        }
        else
        {
            if(b>=1&&b<=12)
            {
                if(c>=1&&c<=monthday1[b])
                {
                    r[e].year=year;
                    r[e].b=b;
                    r[e].c=c;
                    e++;
                }

            }
        }
    }
    return;
}
int main()
{
    int a[5];
    int i;
    for(i=0; i<3; i++)
    {
        cin>>a[i];
        getchar();
    }
    fun(a[0],a[1],a[2]);
    fun(a[2],a[1],a[0]);
    fun(a[2],a[0],a[1]);
    sort(r,r+e,cmp);
    for(i=0; i<e; i++)
    {
        cout<<r[i].year<<'-';
        if(r[i].b<10)
            cout<<'0'<<r[i].b;
        else
            cout<<r[i].b;
        if(r[i].c<10)
            cout<<"-0"<<r[i].c;
        else
            cout<<"-"<<r[i].c;
        cout<<endl;
    }
    return 0;
}

包子凑数

小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼，其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼，可以认为是无限笼。

每当有顾客想买X个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼，分别能放3、4和5个包子。当顾客想买11个包子时，大叔就会选2笼3个的再加1笼5个的（也可能选出1笼3个的再加2笼4个的）。

当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼，分别能放4、5和6个包子。而顾客想买7个包子时，大叔就凑不出来了。

小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
输出
一个整数代表答案。如果凑不出的数目有无限多个，输出INF。
例如，
输入：

2  
4  
5   

程序应该输出：

6  

再例如，
输入：

2  
4  
6    

程序应该输出：

INF

样例解释：
对于样例1，凑不出的数目包括：1, 2, 3, 6, 7, 11。
对于样例2，所有奇数都凑不出来，所以有无限多个。

#include 
#include 
#include 
using namespace std;
int fun(int a,int b)
{
    return b?fun(b,a%b):a;
}
int main()
{
    int n,i,j;
    cin>>n;
    int a[110];
    for(i=0;i<n;i++)
        cin>>a[i];
    int dp[11000];
    memset(dp,0,sizeof(dp));
    dp[0]=1;
    int g=a[0],re=0;
    for(i=1;i<n;i++)
        g=fun(g,a[i]);
    if(g!=1)
        cout<<"INF"<<endl;
    else{
        for(i=0;i<n;i++)
            for(j=a[i];j<=10000;j++)
            dp[j]=max(dp[j],dp[j-a[i]);
        for(i=1;i<=10000;i++)
            if(dp[i]==0)
            re++;
        cout<<re<<endl;
    }
    return 0;
}

#include 
#include 
#include 
using namespace std;

int main()
{
    int n,i,j;
    cin>>n;
    int dp[20000];
    memset(dp,0,sizeof(dp));
    dp[0]=1;
    int a[110];
    for(i=0; i<n; i++)
        cin>>a[i];
    for(i=0; i<n; i++)
        for(j=0; j<=10000; j++)
            if(dp[j])
                dp[j+a[i]]=1;
    bool flag=false;
    int num=0;
    for(i=a[n-1]; i<=10000; i++)
    {
        if(dp[i])
            num++;
        else
            num=0;
        if(num==a[0])
        {
            flag=true;
            break;
        }
    }
    if(!flag)
        cout<<"INF"<<endl;
    else
    {
        num=0;
        for(i=0; i<=10000; i++)
            if(!dp[i])
                num++;
        cout<<num<<endl;
    }
    return 0;
}

分巧克力

儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力，其中第i块是Hi x Wi的方格组成的长方形。

为了公平起见，小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足：

1. 形状是正方形，边长是整数  
2. 大小相同  

例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小Hi计算出最大的边长是多少么？

输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。

输出
输出切出的正方形巧克力最大可能的边长。

样例输入：

2 10  
6 5  
5 6  

样例输出：

2

思路：二分！！

#include 

using namespace std;
struct food
{
    int h,w;
};
int n,k;
food f[110000];
bool judge(int mid)
{
    int sum=0;
    for(int i=0; i<n; i++)
        sum=sum+(f[i].h/mid)*(f[i].w/mid);
    if(sum>=k)
        return true;
    else
        return false;
}
int main()
{
    cin>>n>>k;
    int i;
    for(i=0; i<n; i++)
        cin>>f[i].h>>f[i].w;
    int low=1,high=100000,mid;
    while(low<high-1)
    {
        mid=(low+high)/2;
        if(judge(mid))
            low=mid;
        else
            high=mid;
    }
    cout<<mid-1<<endl;
    return 0;
}

k倍区间

给定一个长度为N的数列，A1, A2, … AN，如果其中一段连续的子序列Ai, Ai+1, … Aj(i <= j)之和是K的倍数，我们就称这个区间[i, j]是K倍区间。

你能求出数列中总共有多少个K倍区间吗？

输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100000)

输出
输出一个整数，代表K倍区间的数目。

例如，
输入：

5 2
1  
2  
3  
4  
5  

程序应该输出：

6

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 2000ms
思路：(sum[j]-sum[i])%k <==> sum[j]%k=sum[i]%k;

#include 
#include 
#include 
using namespace std;
int fun(int t)
{
    if(t==1)
        return 1;
    return fun(t-1)+t;
}
int main()
{
    int n,k,i;
    cin>>n>>k;
    int a[110000],sum=0,re[110000];
    memset(re,0,sizeof(re));
    for(i=0;i<n;i++)
    {
        cin>>a[i];
        sum=(sum+a[i]%k)%k;
        re[sum]++;
    }
    int ma=0;
    for(i=0;i<=100000;i++)
        ma=max(ma,re[i]);
    cout<<fun(ma)<<endl;
    return 0;
}