串匹配一：KMP算法

蛮力算法

蛮力串匹配算法是最直接和最直观方法。

蛮力算法.png

int BFmatch(const string& txt, const string& pat)
{
    size_t N = txt.size();    // 文本串长度
    size_t M = pat.size();    // 模式串长度
    
    int i, j;
    for (i = 0; i <= N-M; i++) {
        for (j = 0; j < M; j++) {
            if (txt[i+j] != pat[j])
                break;
        }
        if (j == M)
            return i;
    }

    return -1;   // 匹配失败返回-1 
}

理论上讲，蛮力算法至多迭代(n - m + 1)次，且每次迭代最多需要比较m次比对。所以总共需要(n - m + 1) * m次比对。因为m << n，所以渐进时间复杂度n*m。

KMP算法

KMP.png

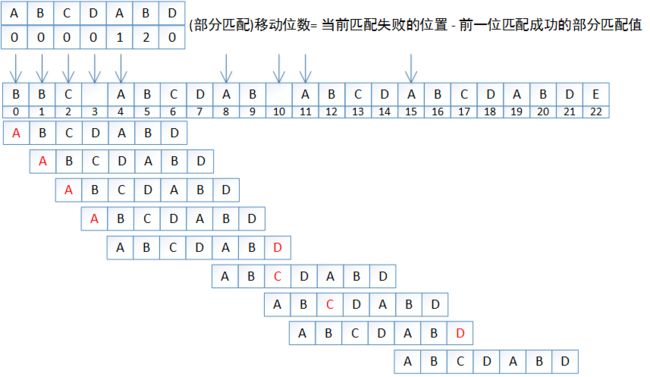
现在D不匹配，按照蛮力匹配的方法，我们下一步要做的就是i = i+1来进行新一轮的匹配。

但是我们已经知道前面6个字符是"ABCDAB"（因为模式串前6个字符是匹配成功的）。KMP算法就是，设法利用这个已知信息，不要把搜索位置移回已经比较过的位置，继续把它向后移，这样就提高了效率。

现在引入一个"部分匹配表"。

部分匹配表.png

利用部分匹配表匹配.png

现在介绍"部分匹配表"是怎么来的。

• 字符串前缀和后缀

  如字符串"ababc"，不考虑空字符
  所有的前缀有：a，ab，aba，abab
  所有的后缀有：c， bc，abc，babc

"部分匹配值"就是"前缀"和"后缀"集合中最长的共有元素的长度。以"ABCDABD"为例：

【1】"A"的前缀和后缀都为空。

【2】"AB"的前缀为[ A ]，后缀为[ B ]，共有元素长度为0。

【3】"ABC"的前缀为[ A, AB]，后缀为[C, BC]，共有元素长度为0。

【4】"ABCD"的前缀为[ A, AB, ABC ]，后缀为[ D, CD, BCD ]，共有元素长度为0。

【5】"ABCDA"的前缀为[ A, AB, ABC, ABCD ]，后缀为[ BCDA, CDA, DA, A ]，共有元素为"A"，长度为1。

【6】"ABCDAB"的前缀为[ A, AB, ABC, ABCD, ABCDA ]，后缀为[ B, AB, DAB, CDAB, BCDAB ]，共有元素为"AB"，长度为2。

【7】"ABCDABD"的前缀为[ A, AB, ABC, ABCD, ABCDA, ABCDAB ]，后缀为[ D, BD, ABD, DABD, CDABD, BCDABD ]，共有元素的长度为0。

所以部分匹配的实质就是：字符串头部和尾部会有相同的子字符串，比如"ABCDABD"之中首尾的"AB"。当匹配最后一个D失败时，第一个AB的匹配就可以移动到第2个AB重新开始。

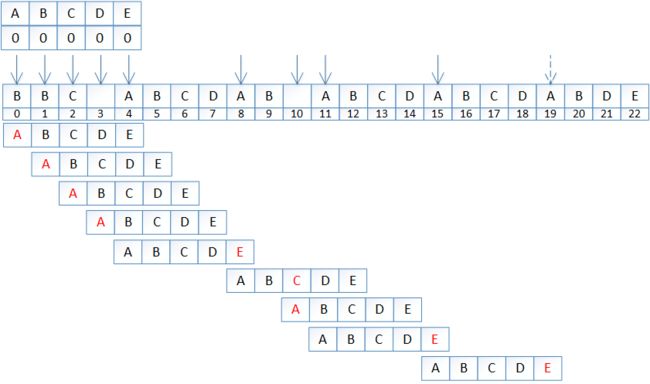
那么如果模式串头部和尾部没有相同的子字符串，KMP算法就不起作用了呢？
答案是否的。当没有相同的子字符串时，如果存在部分匹配，那么我们就可以一次跳过已经部分匹配的字符，因为它们的不会像上一种情况有"利用价值"

KMP2.png

实现

/* 以下代码只为实现KMP核心思想，未考虑边界测试 */
std::vector makeNext(const std::string& pat)
{
    int N = pat.size();
    std::vector next(N, 0);
    
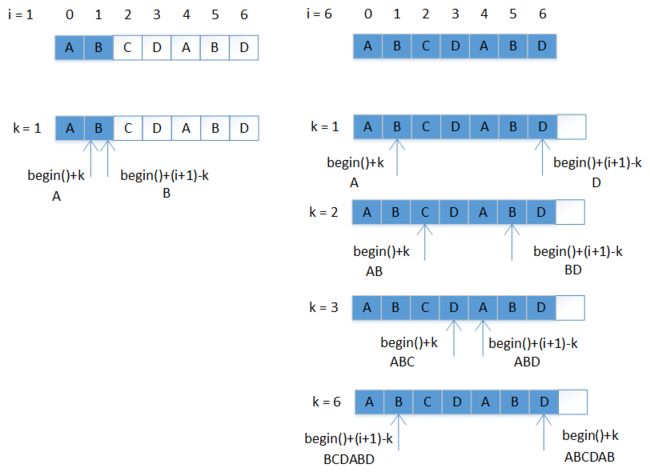
    for (int i = 1; i < N; i++) {
        for (int k = 1; k <= i; k++) {
            if (std::equal(pat.begin(), pat.begin()+k, pat.begin()+(i+1)-k))
                next[i] = k;
        }
    }   
    return next;
}

next.png

/* 以下代码只为实现KMP核心思想，未考虑边界测试 */
int KMPmatch(const std::string& txt, const std::string& pat)
{
    int n = txt.size();
    int m = pat.size();
    std::vector next = makeNext(pat);
    bool flag = false;    // 记录部分匹配的标志位

    int i, j, skip;
    for (i = 0; i <= n-m; i += skip) {
        for (j = 0; j < m; j++) {
            if (txt[i+j] != pat[j]) {  
                skip = flag ? j-next[j-1] : 1; //根据这一轮是否有部分匹配，得到i要增加的值
                flag = false;
                break;
            } else {
                flag = true;      // 记录这一轮是否有部分匹配。
            }
        }
        if (j == m)
            return i;
    }

    return -1;
}

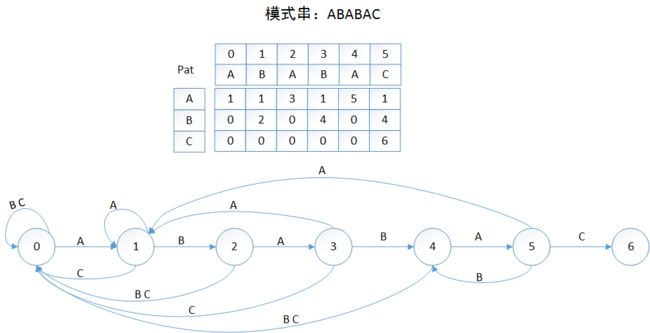
附：KMP算法与DFA

DFA.png

参考资料
[1] 《算法》4th
[2] http://www.cnblogs.com/c-cloud/p/3224788.html