矩阵的奇异值分解(SVD )及其应用
摘要:奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction PCA ,做数据压缩(以图像压缩为代表)的算法,以及做潜在语义索引LSI算法等。
关键词:奇异值分解 主成分分析(PCA)潜在语义索引LSI
Singular Value Decomposition (SVD) of Matrix and Its Application
Abstract: Singular value decomposition is a method with obvious physical meaning. It can represent a more complex matrix by multiplying smaller and simpler sub-matrices, which describe the importance of the matrix. Characteristics. Just like describing a person, telling others that this person has a thick eyebrow, a square face, a slap in the face, and a black framed glasses, so that a few characteristics of the cockroach, so that there is a comparison in the minds of others A clear understanding, in fact, there are countless kinds of characteristics on the human face. The reason why it can be described is that people are born with very good ability to extract important features, let the machine learn to extract important features, SVD is a The important method. In the field of machine learning, there are quite a few applications that can be related to singular values, such as feature reduction PCA, data compression (represented by image compression), and latent semantic index LSI algorithms.
Keywords:Singular Value Decomposition;Principal Component Analysis (PCA) ;Latent Semantic Index LSI
一、奇异值与特征值基础知识:
特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征。
1 )特征值:
如果说一个向量v 是方阵A的特征向量,将一定可以表示成下面的形式:
Av=λv
这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
A=QΣQ-1
其中 Q 是这个矩阵A的特征向量组成的矩阵,Σ 是一个对角阵,每一个对角线上的元素就是一个特征值。我这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。当矩阵是高维的情况下,那么这个矩阵就是高维空间下的一个线性变换,我们通过特征值分解 得到的前 N 个特征向量,那么就对应了这个矩阵最主要的N 个变化方向。我们利用这前 N个变化方向,就可以近似这个矩阵(变换)。也就是之前说的:提取这个矩阵最重要的特征。总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
2 )奇异值:
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵,比如说有 N 个学生,每个学生有 M 科成绩,这样形成的一个N * M 的矩阵就不可能是方阵,而奇异值分解可以用来干这个事情,奇异值分解是一个能适用于任意的矩阵的一种分解的方法:
A=UΣVT
假设 A 是一个 M * N的矩阵,那么得到的U 是一个M * M 的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个 M * N的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),VT(V的转置 ) 是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量)。将奇异值和特征值是对应起来的首先,将一个矩阵A的转置* A ,将会得到一个方阵,我们用这个方阵求特征值可以得到:
![]()
这里得到的V,就是我们上面的右奇异向量。此外我们还可以得到:
![]()
这里的σ就是上面说的奇异值,u 就是上面说的左奇异向量。奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前 10%甚至 1% 的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解 :
其中r是一个远小于m 、 n的数。
二、奇异值与主成分分析(PCA):
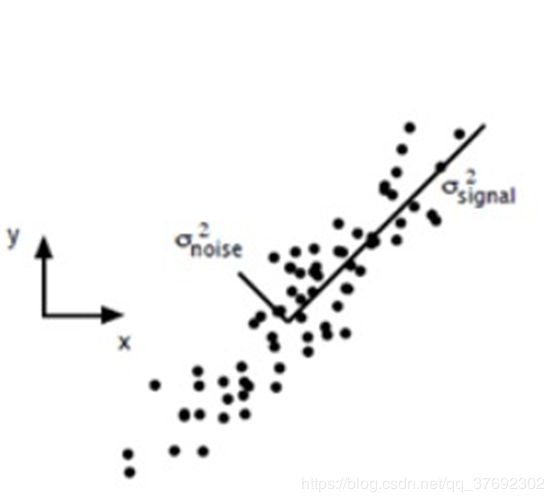
主成分分析在上一节里面也讲了一些,这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量,我们在讲一个东西的稳定性的时候,往往说要减小方差,如果一个模型的方差很大,那就说明模型不稳定了。但是对于我们用于机器学习的数据(主要是训练数据),方差大才有意义,不然输入的数据都是同一个点,那方差就为0了,这样输入的多个数据就等同于一个数据了。以下面这张图为例子:
这个假设是一个摄像机采集一个物体运动得到的图片,上面的点表示物体运动的位置,假如我们想要用一条直线去拟合这些点,那我们会选择什么方向的线呢?当然是图上标有signal的那条线。如果我们把这些点单纯的投影到 x轴或者y轴上,最后在x 轴与y轴上得到的方差是相似的(因为这些点的趋势是在45度左右的方向,所以投影到x 轴或者y 轴上都是类似的),如果我们使用原来的xy坐标系去看这些点,容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化,横轴变成了signal的方向,纵轴变成了noise的方向,则就很容易发现什么方向的方差大,什么方向的方差小了。
一般来说,方差大的方向是信号的方向,方差小的方向是噪声的方向,我们在数据挖掘中或者数字信号处理中,往往要提高信号与噪声的比例,也就是信噪比。对上图来说,如果我们只保留signal方向的数据,也可以对原数据进行不错的近似了。
PCA 的全部工作简单点说,就是对原始的空间中顺序地找一组相互正交的坐标轴,第一个轴 是使得方差最大的,第二个轴是在与第一个轴正交的平面中使得方差最大的,第三个轴是在与第 1 、2个轴正交的平面中方差最大的, 这样假设在N 维空间中,我们可以找到 N 个这样的坐标轴,我们取前r个去近似这个空间,这样就从一个N维的空间压缩到 r 维的空间了,但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
还是假设我们矩阵每一行表示一个样本,每一列表示一个feature,用矩阵的语言来表示,将一个 m * n的矩阵A的进行坐标轴的变化,P就是一个变换的矩阵从一个N 维的空间变换到另一个N维的空间,在空间中就会进行一些类似于旋转、拉伸的变化。
![]()
而将一个m * n的矩阵A变换成一个m * r的矩阵,这就会使得本来有个nfeature的,变成了有r个 feature了(r 但是这个怎么和SVD扯上关系呢?之前谈到,SVD得出的奇异向量也是从奇异值由大到小排列的,按PCA的观点来看,就是方差最大的坐标轴就是第一个奇异向量,方差次大的坐标轴就是第二个奇异向量 我们回忆一下之前得到的SVD式子: 在矩阵的两边同时乘上一个矩阵V,由于V是一个正交的矩阵,所以V转置乘以V 得到单位阵I,所以可以化成后面的式子 Am*nVr*n≈Um*rΣr*rVTr*nVr*n 将后面的式子与A * P那个 m * n 的矩阵变换为m * r的矩阵的式子对照看看,在这里,其实V 就是P,也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵,也就是对列进行压缩,如果我们想对行进行压缩(在PCA 的观点下,对行进行压缩可以理解为,将一些相似的 sample合并在一起,或者将一些没有太大价值的sample去掉),同样可以写出一个通用的行压缩例子: Pr*mAm*n=Ar*n 这样就从一个m行的矩阵压缩到一个r行的矩阵了,对SVD来说也是一样的,我们对SVD 分解的式子两边乘以U的转置 UT: 这样我们就得到了对行进行压缩的式子。可以看出,其实PCA几乎可以说是对SVD 的一个包装,如果我们实现了SVD,那也就实现了 PCA了,而且有了SVD,我们就可以得到两个方向的PCA ,如果我们对ATA进行特征值的分解,只能得到一个方向PCA 。 三、奇异值与潜在语义索引LSI : 潜在语义索引(Latent Semantic Indexing)与 PCA不太一样,至少不是实现了SVD就可以直接用的,不过 LSI也是一个严重依赖于 SVD 的算法,吴军老师在矩阵计算与文本处理中的分类问题中谈到:“三个矩阵有非常清楚的物理含义。第一个矩阵 X 中的每一行表示意思相关的一类词,其中的每个非零元素表示这类词中每个词的重要性(或者说相关性),数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章,其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此,我们只要对关联矩阵A进行一次奇异值分解,w我们就可以同时完成了近义词分类和文章的分类。(同时得到每类文章和每类词的相关性)。 举一个例子来说明一下: 这就是一个矩阵,不过不太一样的是,这里的一行表示一个词在哪些title中出现了(一行就是之前说的一维feature ),一列表示一个title中有哪些词,(这个矩阵其实是我们之前说的那种一行是一个sample 的形式的一种转置,这个会使得我们的左右奇异向量的意义产生变化,但是不会影响我们计算的过程)。比如说 T1 这个title中就有guide、investing、market、stock 四个词,各出现一次,我们将这个矩阵进行SVD,得到下面的矩阵: 左奇异向量表示词的一些特性,右奇异向量表示文档的一些特性,中间的奇异值矩阵表示 左奇异向量的一行与右奇异向量的一列的重要程序,数字越大越重要。继续看这个矩阵还可以发现一些有意思的东西,首先,左奇异向量的第一列表示每一个词的出现频繁程度,虽然不是线性的,但是可以认为是一个大概的描述,比如文档book是0.15对应中出现的2次,investing是0.74对应了文档中出现了9次,rich是 0.36对应文档中出现了 3 次;其次,右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似,比如说,T6是0.49,出现了5个词,T2是0.22,出现了2个词。然后我们反过头来看,我们可以将左奇异向量和右奇异向量都取后2 维(之前是3维的矩 阵),投影到一个平面上,可以得到: 在图上,每一个红色的点,都表示一个词,每一个蓝色的点,都表示一篇文档,这样我们可以对这些词和文档进行聚类,比如说stock和 market可以放在一类,因为他们老是出现在一起, real 和estate可以放在一类,dads,guide这种词就看起来有点孤立了,我们就不对他们进行合并了。按这样聚类出现的效果,可以提取文档集合中的近义词,这样当用户检索文档的时候,是用语义级别(近义词集合)去检索了,而不是之前的词的级别。这样一减少我们的检索、存储量,因为这样压缩的文档集合和PCA是异曲同工的,二可以提高我们的用户体验,用户输入一个词,我们可以在这个词的近义词的集合中去找,这是传统的索引无法做到的。 ![]()
![]()
![]()
![]()
参考文献