形式语言与自动机 练习题总结
例2
请设计 DFA, 在任何由 0 和 1 构成的串中, 接受含有 01 子串的全部串
{0,1}的子串全部串有:0,1,01,故本题有三种状态
- 未发现 01, 即 0 没有出现过;
- 未发现 01, 但刚刚读入字符是 0;
- 已经发现了 01.
因此 DFA A 可定义为:A = ({q1,q2,q3},{0,1},δ,q1,{q3})
其中 δ 为:
δ(q1,1) = q1 δ(q2,1) = q3 δ(q3,1) = q3
δ(q1,0) = q2 δ(q2,0) = q2 δ(q3,0) = q3
将此DFA用状态转移图表示:其中q1为初始状态
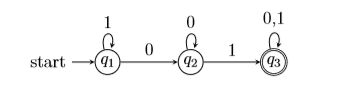
将此DFA用状态转移表表示:
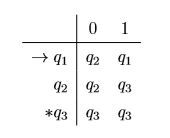
求解接受全部含有 01 子串的 DFA, ˆ δ 处理串 0101 的过程
解题过程借助如上的状态转移图

注意:ˆ δ(q0,ε) = δ(q0,0)
例3.
若 Σ = {0,1}, 给出接受全部含有奇数个 1 的串 DFA
状态有两个:q0→偶数个1,q1→奇数个1,其中q1为接受状态
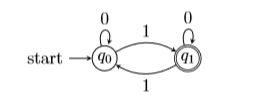
例4.
若 Σ = {0,1}, 给出接受全部含有偶数个 0 和偶数个 1 的串 DFA
接受状态:00,11,1100,111100,…
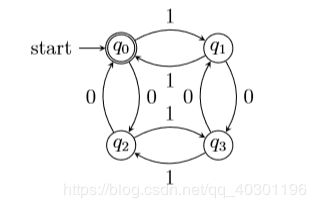
例5.
对任何状态 q 及字符串 x 和 y, 证明 ˆ δ(q,xy) = ˆ δ(ˆ δ(q,x),y)
@注意,类似此类证明,均对y进行数学归纳法
1.y = ε 时,i
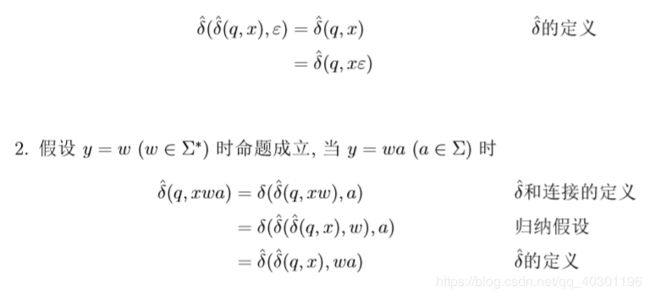
例7.
由 0 和 1 构成的串中, 接受全部以 01 结尾的串, 如何设计 DFA?
q0: XX11
q1:XXX0
q2:XX01
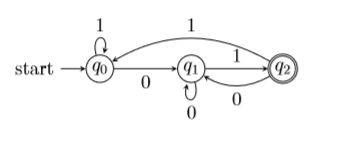
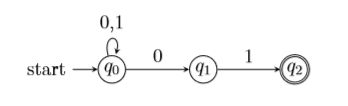
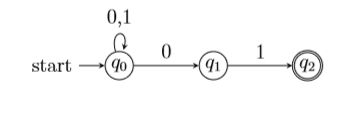
续例7. 接受全部以 01 结尾的串的 NFA.
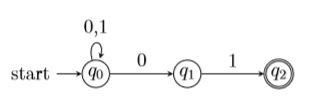
五元组为 A = ({q0,q1,q2},{0,1},δ,q0,{q2}),
转移函数 δ:
δ(q0,0) = {q0,q1} δ(q1,0) = ∅ δ(q2,0) = ∅
δ(q0,1) = {q0} δ(q1,1) = {q2} δ(q2,1) = ∅
续例7.
接受 01 结尾的串的 NFA, ˆ δ 处理 00101 时每步的状态转
- ˆ δ(q0,ε)={q0}
- ˆ δ(q0,0) = δ(q0,0) = {q0,q1}
- ˆ δ(q0,00) = δ(q0,0)∪δ(q1,0) = {q0,q1}∪∅ = {q0,q1}
- ˆ δ(q0,001) = δ(q0,1)∪δ(q1,1) = {q0}∪{q2} = {q0,q2}
- ˆ δ(q0,0010) = δ(q0,0)∪δ(q2,0) = {q0,q1}∪∅ = {q0,q1}
- ˆ δ(q0,00101) = δ(q0,1)∪δ(q1,1) = {q0}∪{q2} = {q0,q2}
因为 q2 是接受状态, 所以 NFA 接受 00101
例8.
设计 L = {w ∈{0,1}∗ | w 的首尾字符相同.} 的 NFA
续例11.
L = {w ∈{0,1}∗ | w 倒数 3 个字符至少有一个是 1} 的 NFA.
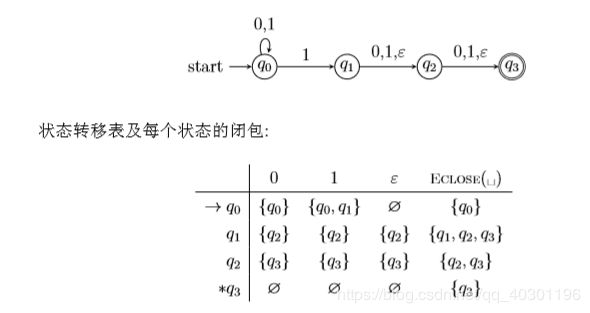
例4.
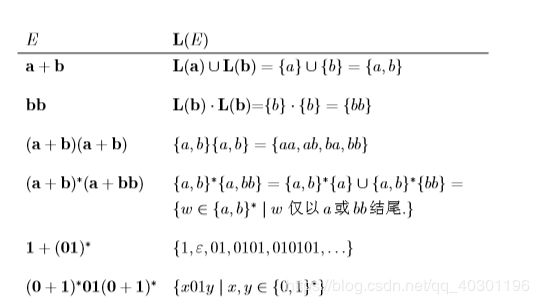
例5.
给出正则表达式 (aa)∗(bb)∗b 定义的语言
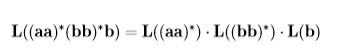
例6.
Design regular expression for L = {w | w consists of 0’s and 1’s, and the third symbol from the right end is 1.}
(0+1)∗1(0+1)(0+1)
例7.
Design regular expression for L = {w | w ∈{0,1}∗ and w has no pair of consecutive 0’s.}
![]()
例9.
将如图 DFA 转换为正则表达式.
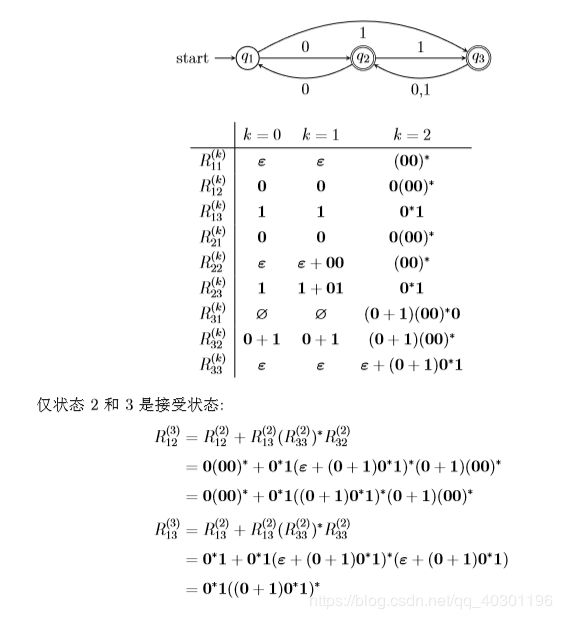

例10.
利用状态消除法, 设计下图自动机的正则表达式.
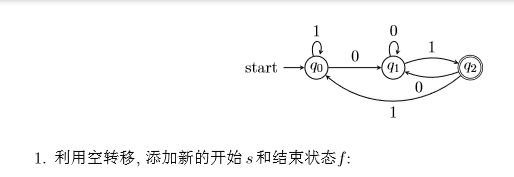
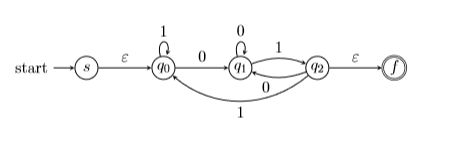
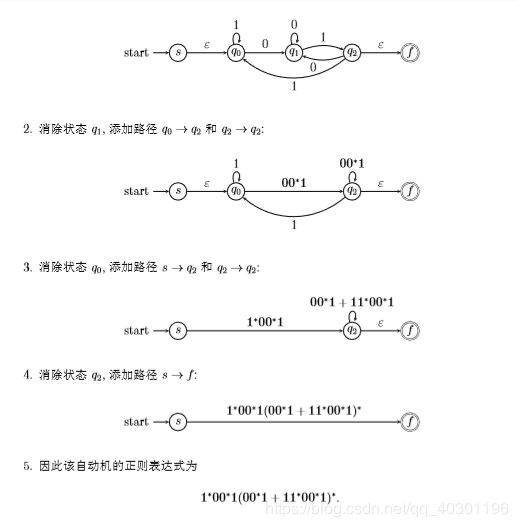
例11.
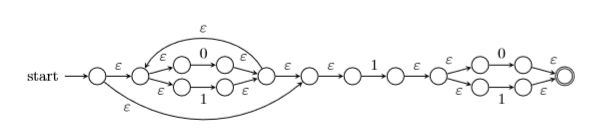
正则表达式 (0+1)∗1(0+1) 构造为 ε-NFA
例12. 判断 (L + M)∗ = (L∗M∗)∗.
- 将 L 和 M 替换为 a 和 b;
- (a+b)∗ ?= (a∗b∗)∗;
- 因为 L((a+b)∗) = L((a∗b∗)∗);
- 所以 (L + M)∗ = (L∗M∗)∗.
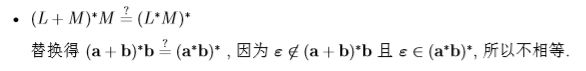
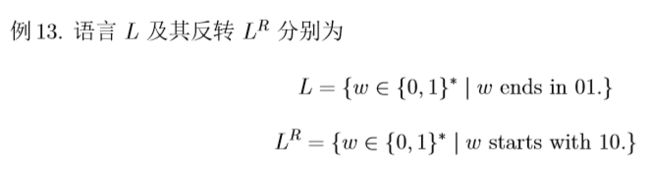
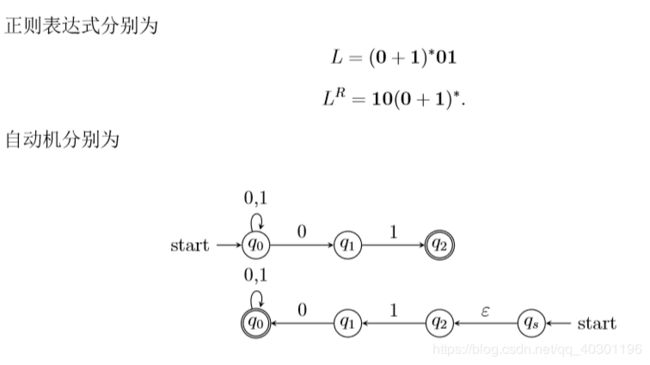
例16.
若语言 L = (00+1)∗, 同态 h : {a,b}→{0,1}∗
为h(a) = 01, h(b) = 10,
请证明 h−1(L) = (ba)∗
- 若w以a开头,则h(w) starts with 01,h(w) not in L;
- if w ends with b, then h(w) end with 10, h(w) not in L;
- if w contains consecutive aa, then h(w) contains 0101, h(w) not in L;
- if w contains consecutive bb, then h(w) contains 1010, h(w) not in L;
So, h-1(L)=(ba)*
例17.
For a language L, define head(L) to be the set of all prefixes of strings in L. Prove that if L is regular, so is head(L)
