为什么我们的神经网络需要激活函数

如果你正在读这篇文章，那么很可能你已经知道什么是神经网络，什么是激活函数，但是，一些关于机器学习的入门课程并不能很清楚地说明，为什么我们需要这些激活函数。我们需要它们吗?没有它们，神经网络还能工作吗?

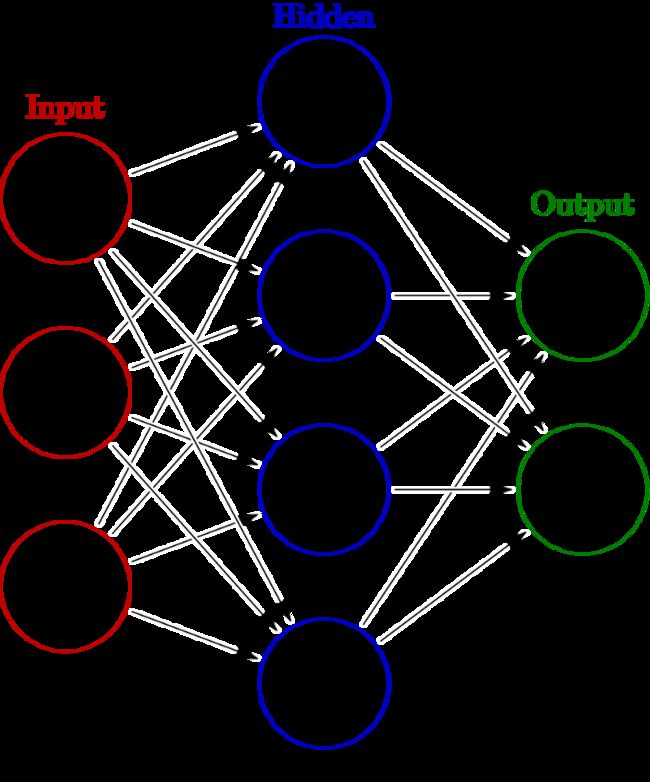
首先让我们回顾一下关于神经网络的一些事情。它们通常被可视化地表示为一个类似图表的结构，如下图所示:

如上图所示，神经网络有3层:输入层、隐藏层、输出层，共3、4、2个神经元。
输入层的节点数量与数据集的特性数量相同。对于隐藏层，您可以自由选择需要多少节点，并且可以使用多个隐藏层。

网络中的每个神经元，除了那些在输入层的神经元，可以被认为是一个线性分类器，它将前一层神经元的所有输出作为输入，并计算这些输出加上一个偏置项的加权和。然后，下一层的神经元将前一层线性分类器计算的值作为输入，然后计算这些值的加权和，依此类推。我们希望，通过以这种方式结合线性分类器，我们可以构建更复杂的分类器，可以代表我们的数据中的非线性模式。

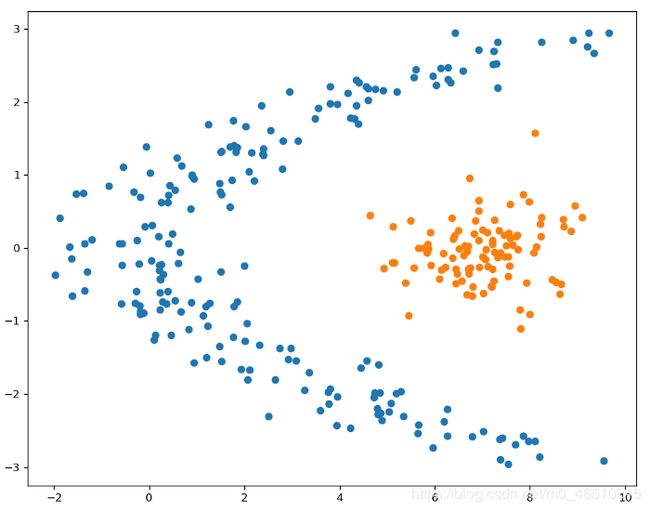
让我们看看下面的例子数据集:

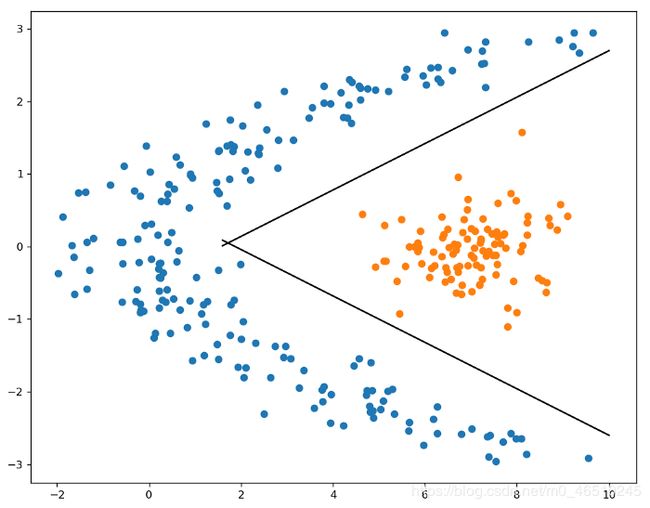
这个数据集不是线性可分的，我们不能将一个类从另一个通过一条线分开。但我们可以通过使用两条线作为决策边界来实现这种分离。

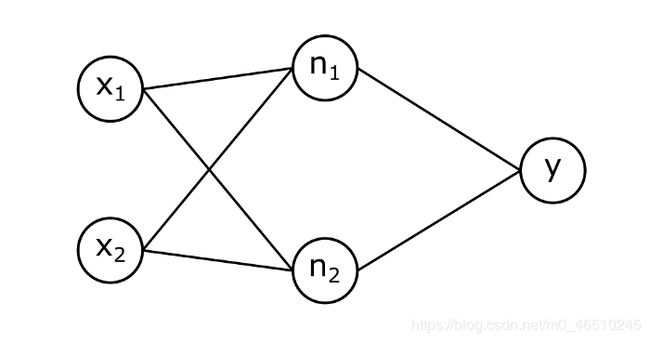
所以，我们可能认为两个中间神经元可以完成这个工作。这两个神经元将学习上图中的两条分离线。然后我们需要一个输出神经元它将之前的两个神经元作为输入，这样它就能正确地进行分类。

对于最后一个做正确分类的神经元，它需要n1和n2隐藏神经元的输出是线性可分的，如果我们把它们画在一个二维平面上。上面画的两条线有方程:

这意味着这两个隐藏的神经元正在计算输入x1和x2的如下线性组合:

我们画出n1和n2看看它们是否有用。

我们对我们的小神经网络感到失望。n1和n2的输出仍然不是线性可分的，因此输出神经元不能正确分类。那么，问题是什么呢?

问题是，任何线性函数的线性组合仍然是线性的，在一张纸上证明它是正确的并不难。这一事实的证据在本文的结尾。所以，不管我们用了多少层或多少神经元，按照我们目前的方式，我们的神经网络仍然只是一个线性分类器。

我们需要更多的东西。我们需要将每个神经元计算出的加权和传递给一个非线性函数，然后将这个函数的输出看作那个神经元的输出。这些函数称为激活函数，它们在允许神经网络学习数据中的复杂模式时非常重要。

[1] 已经证明，具有2层(输入层除外)和非线性激活函数的神经网络，只要在这些层中有足够多的神经元，就可以近似任何函数。那么，如果只有两层就够了，为什么人们现在还在使用更深层次的网络呢?嗯，仅仅因为这两层网络“能够”学习任何东西，这并不意味着它们很容易优化。在实践中，如果我们的网络产能过剩，他们就会给我们提供足够好的解决方案，即使他们没有尽可能地优化。

还有更多种类的激活函数，我们想在上面的示例中使用其中的两种。它们分别是ReLU(直线单元)和tanh(双曲正切)，如下图所示。

如果我们在示例中使用ReLU激活，将会发生什么?下图是应用ReLU激活后n1和n2神经元的输出。

现在，我们的这两类点可以用直线分开，这样输出神经元就可以正确地对它们进行分类。

如果我们使用tanh激活，也会发生类似的事情，但这次我们的点之间的差距更大。

同样，输出神经元可以正确地分类这些点。

这里有一个简单的数学证明，证明任何线性函数的线性组合仍然是线性的:

其中a0, a1，…，an是不依赖于输入x1，…，xn的常数。

我希望这篇文章对你有用，谢谢阅读!

参考

[1] Cybenko, G.V. (2006). “Approximation by Superpositions of a Sigmoidal function”. In van Schuppen, Jan H. (ed.). Mathematics of Control, Signals, and Systems. Springer International. pp. 303–314.

作者：Dorian Lazar

deephub翻译组