旋转卡壳详解

注:本文章参考自:https://blog.csdn.net/wang_heng199/article/details/74477738

问题描述

基本问题为O(n)求凸n角形的对踵点,而由该问题可以引申出许多的难题，他们包括:

• 计算距离

  • 凸多边形直径
  • 凸多边形宽
  • 凸多边形间最大距离
  • 凸多边形间最小距离

• 外接矩形

  • 最小面积外接矩形
  • 最小周长外接矩形

问题求解

计算距离

• 凸多边形直径
  我们将一个多边形上任意两点间的距离的最大值定义为多边形的直径。 确定这个直径的点对数可能多于一对。 事实上， 对于拥有 n 个顶点的多边形， 就可能有 n 对“直径点对”存在。
  
  一个多边形直径的简单例子如左图所示。 直径点对在图中显示为被平行线穿过的黑点 （红色的一对平行线）. 直径用浅蓝色高亮显示。
  显然， 确定一个凸多边形 P 直径的点对不可能在多边形 P 内部。 故搜索应该在边界上进行。 事实上， 由于直径是由多边形的平行切线的最远距离决定的， 所以我们只需要查询对踵点。 Shamos (1978) 提供了一个 O(n) 时间复杂度计算n点凸包对踵点对的算法。直径通过遍历顶点列表， 得到最大距离即可。

算法描述
1. 计算多边形y方向的端点，我们称之为 ymin y m i n 和 ymax y m a x
2. 通过 ymin y m i n 和 ymax y m a x 构造两条水平切线。由于他们已经是一对对踵点，计算他们之间的距离并维护一个当前的最大值。
3. 同时旋转两条线直到其中一条与多边形的一边重合。
4. 一个新的对踵点对此时产生。计算新的距离，并和当前的最大值比较，大于当前最大值则更新。
5. 重复步骤3和步骤4的过程直到再次产生对踵点对。
6. 输出确定最大直径的对踵点对。

代码:

void solve2(int num)
{
    int ymax=-1e5,ymin=1e5;
    int ymaxidx,yminidx;
    for(int i=1;i<=num;i++)
    {
        if(ch[i].y>ymax)
        {
            ymax=ch[i].y;
            ymaxidx=i;
        }
        if(ch[i].yy;
            yminidx=i;
        }
    }
    int ans=dis2(ch[ymaxidx]-ch[yminidx]);
    ch[num+1]=ch[1];
    for(int t=1;t<=num;t++,yminidx=yminidx%num+1)
    {
        while(xmult(ch[yminidx+1],ch[ymaxidx+1],ch[yminidx])>xmult(ch[yminidx+1],ch[ymaxidx],ch[yminidx]))ymaxidx=ymaxidx%num+1;
        ans=max(ans,dis2(ch[ymaxidx]-ch[yminidx]));
        ans=max(ans,dis2(ch[ymaxidx]-ch[yminidx+1]));
    }
    printf("%d\n",ans);
}

• 凸多边形宽度
  凸多边形的宽度定义为平行切线间的最小距离。这个定义从宽度这个词已经略有体现。虽然凸多边形的切线有不同的方向，并且每个方向的宽度通常是不同的。但幸运的是，不是所有的方向都要计算。
  我们假设存在一个线段[a,b],以及两条通过a和b的平行线，通过绕着这两个点旋转这两条线，使他们的距离递增或递减，特别的，总存在一个特定的方向使得两条线段的距离通过旋转变小。
  这个简单的结论可以用到计算宽度中:不是所有的方向都要考虑，假设给定一个凸多边形后，同时还有两条平行切线。如果他们都未与边重合，那么我们总能通过旋转来减少他们的距离，因此，两条平行切线只有在其中至少一条与边重合的情况下才能确定多边形的宽度。
  这就意味着”对踵点 点-边”以及“边-边”对需要在计算宽度过程中被考虑。
  
  一个凸多边形宽度的示意图。 直径对如图由平行切线（红线）穿过的黑点所示。 直径如高亮的淡蓝色线所示。

一个与计算直径问题非常相似的算法可以通过遍历多边形对踵点对列表得到， 确定顶点-边以及边-边对来计算宽度。 选择过程如下:
1. 计算多边形y方向的端点，我们称之为 ymin y m i n 和 ymax y m a x
2. 通过 ymin y m i n 和 ymax y m a x 构造两条水平切线，如果一条(或者两条)与边重合，那么一个”对踵点 点-边”或者”边-边”对已经确定，此时计算两线间的距离，并且存为当前最小距离。
3. 同时旋转两条线直到其中一条线与多边形的一边重合。
4. 一个新的对踵点对(“点-边或者边-边”)此时产生。计算新的距离，并和当前的最小值比较，小于当前最小值则更新。
5. 重复3和4的过程知道再次达到最初的平行线的位置。
6. 将获得的最小值的对作为确定宽度的对输出。

代码与上面类似，略。

• 凸多边形间的最大距离

给定两个凸多边形P和Q，目标是需要找到点对(p,q)(p属于P,q属于Q)使得他们之间的距离最大。
很直观的，这些点不属于他们的内部。这个条件事实上与直径问题非常类似。

两凸多边形P和Q间最大距离由多边形对踵点对确定。
虽然说法一样，但是这个定义与给定凸多边形的对踵点对的不同。
与凸多边形间的对踵点对本质上的区别在于切线是有向且反向的，下图展示了一个例子:

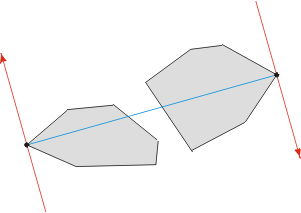
注:虽然意思相同，但博主的代码所描述的切线方向与本图相反，即所代表的面积都为切线的左边方向而不是图中的右边方向。
上述结论暗示不单纯只是顶点对需要检测，而仅仅是特定的顶点对需要被考虑，实际上他们只间测一个基于旋转卡壳模式的算法确立的平行切线。
考虑如下的算法，算法的输入是两个分别有m和n个逆时针给定顶点的凸多边形P和Q。
1. 计算P上y坐标最小的顶点(称为yminP)和Q上y坐标值最大的顶点(称为ymaxQ)。
2. 为多边形在yminP和ymaxQ处构造两条切线LP和LQ使得他们对应的多边形都位于他们的左侧，此时LP和LQ拥有不同的方向，并且yminP和ymaxQ成为多边形间的一个对踵点对。
3. 计算距离(yminP和ymaxQ)并且将其维护一个最大值。
4. 逆时针同时旋转平行线直到其中一个与其所在的多边形的边重合。
5. 一个新的对踵点对产生了，计算新距离，与当前最大值比较，如果大于当前最大值则更新。如果两条线同时与边发生重合，此时总共四个对踵点对(点-点)(先前顶点和新顶点的组合)需要考虑在内。
6. 重复执行步骤4和步骤5，直到新的点对为(yminP,ymaxQ).
7. 输出最大距离。

• 凸多边形间的最小距离

给定两个非连接(比如不相交)的凸多边形P和Q，目标是找到拥有最小距离的点对(p,q)(p属于P且q属于Q)。
事实上，多边形非连接十分重要，因为我们所说的多边形包含其内部，如果多边形相交，那么最小距离就变得没有意义了。然而，对于这个问题的另一版本，凸多边形顶点间最小距离对于相交和非相交的情况都有解存在。

回到我们的主问题：直观的，确定最小距离的点不可能包含在多边形内部。与最大距离问题相似，我们有如下结论:

两个凸多边形P和Q之间的最小距离由多边形间的对踵点对确立。存在凸多边形三种多边形间的对踵点对， 因此就有三种可能存在的最小距离模式：
1. “顶点-顶点”的情况
2. “顶点-边”的情况
3. “边-边”的情况

换句话说， 确定最小距离的点对不一定必须是顶点。 下面的三个图例表明了以上结论：

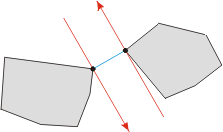
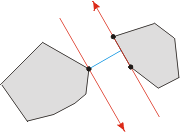
注:虽然意思相同，但博主的代码所描述的切线方向与本图相反，即所代表的面积都为切线的左边方向而不是图中的右边方向。
给定结果， 一个基于旋转卡壳的算法自然而然的产生了:
考虑如下的算法， 算法的输入是两个分别有 m 和 n 个逆时针给定顶点的凸多边形 P 和 Q。
1. 计算 P 上 y 坐标值最小的顶点（称为 yminP ） 和 Q 上 y 坐标值最大的顶点（称为 ymaxQ）。
2. 为多边形在 yminP 和 ymaxQ 处构造两条切线 LP 和 LQ 使得他们对应的多边形位于他们的左侧。 此时 LP和 LQ 拥有不同的方向， 并且 yminP 和 ymaxQ 成为了多边形间的一个对踵点对。
3. 计算距离(yminP,ymaxQ) 并且将其维护为当前最小值。
4. 逆时针同时旋转平行线直到其中一个与其所在的多边形的边重合。
5. 如果只有一条线与边重合， 那么只需要计算“顶点-边”对踵点对和“顶点-顶点”对踵点对距离(点到线段的距离)。 都将他们与当前最小值比较， 如果小于当前最小值则进行替换更新。 如果两条切线都与边重合， 则计算线段到线段的距离。 所有的这些距离都与当前最小值进行比较， 若小于当前最小值则更新替换。
6. 重复执行步骤4和步骤5， 直到新的点对为(yminP,ymaxQ)。
7. 输出最大距离。

代码:

double solve(Point *a,int anum,Point *b,int bnum)
{
    int i;
    double tmp,res=1e10;
    a[anum+1]=a[1],b[bnum+1]=b[1];
    int p,q;
    double ymin=1e5,ymax=-1e5;
    for(i=1;i<=anum;i++)
    {
        if(a[i].yfor(i=1;i<=bnum;i++)
    {
        if(b[i].y>ymax)
        {
            ymax=b[i].y;
            q=i;
        }
    }

    for(i=1;i<=anum;i++)
    {
        while(sgn((tmp=((a[p+1]-a[p])^(b[q+1]-a[p]))-((a[p+1]-a[p])^(b[q]-a[p]))))>0)
            q=q%bnum+1;
        if(sgn(tmp)<0)res=min(res,disptoseg(b[q],a[p],a[p+1]));
        else res=min(res,dissegtoseg(a[p],a[p+1],b[q],b[q+1]));
        p=p%anum+1;
        //cout<
    }
    return res;
}

注:在计算时并不知道这两个凸多边形的相对位置，因此可能计算出来的值比最小值大，故在用的时候需要这样:

double tmp=solve(ch1,p1num,ch2,p2num);
printf("%.5f\n",min(tmp,solve(ch2,p2num,ch1,p1num)));

最小距离及最大距离的问题表明了旋转卡壳模型可以用在不同的条件下(与先前的直径和宽度问题比较)。这个模型可以用在两个凸多边形的问题上。

“最小盒子”问题(最小面积外接矩阵)通过同一多边形的两个正交切线集合展示了另一种条件下的旋转卡壳的应用。

外接矩形

• 凸多边形最小面积外接矩阵

给定一个凸多边形 P ， 面积最小的能装下 P （就外围而言）的矩形是怎样的呢？ 从技术上说， 给定一个方向， 能计算出 P 的端点并且构由此造出外接矩形。 但是我们需要测试每个情形来获得每个矩形来计算最小面积吗？ 谢天谢地， 我们不必那么干。

对于多边形 P 的一个外接矩形存在一条边与原多边形的边共线。

上述结论有力地限制了矩形的可能范围。 我们不仅不必去检测所有可能的方向， 而且只需要检测与多边形边数相等数量的矩形。

图示上述结论： 四条切线（红色）， 其中一条与多边形一条边重合， 确定了外接矩形（蓝色）。
一个简单的算法是依次将每条边作为与矩形重合的边进行计算。 但是这种构造矩形的方法涉及到计算多边形每条边端点， 一个花费 O(n) 时间（因为有 n 条边）的计算。 整个算法将有二次时间复杂度。

一个更高效的算法已经发现。 利用旋转卡壳， 我们可以在常数时间内实时更新， 而不是重新计算端点。
实际上， 考虑一个凸多边形， 拥有两对和 x 和 y 方向上四个端点相切的切线。 四条线已经确定了一个多边形的外接矩形。 但是除非多边形有一条水平的或是垂直的边， 这个矩形的面积就不能算入最小面积中。
然而， 可以通过旋转线直到条件满足。 这个过程是下属算法的核心。 假设按照顺时针顺序输入一个凸多边形的n 个顶点。

1. 计算全部四个多边形的端点， 称之为 xminP， xmaxP， yminP， ymaxP。
2. 通过四个点构造 P 的四条切线。 他们确定了两个“卡壳”集合。
3. 如果一条（或两条）线与一条边重合， 那么计算由四条线决定的矩形的面积， 并且保存为当前最小值。 否则将当前最小值定义为无穷大。
4. 顺时针旋转线直到其中一条和多边形的一条边重合。
5. 计算新矩形的面积， 并且和当前最小值比较。 如果小于当前最小值则更新， 并保存确定最小值的矩形信息。
6. 重复步骤4和步骤5， 直到线旋转过的角度大于90度。
7. 输出外接矩形的最小面积。

代码:

double solve(int num)
{
    int r=2,q=2,p;
    double res=1e10;
    ch[num+1]=ch[1];
    for(int i=1;i<=num;i++)
    {
        while(sgn(xmult(ch[i+1],ch[r+1],ch[i])-xmult(ch[i+1],ch[r],ch[i]))>0)r=r%num+1;
        while(sgn(dot(ch[i+1],ch[q+1],ch[i])-dot(ch[i+1],ch[q],ch[i]))>0)q=q%num+1;
        if(i==1)p=q;
        while(sgn(dot(ch[i+1],ch[p+1],ch[i])-dot(ch[i+1],ch[p],ch[i]))<=0)p=p%num+1;
        double a=xmult(ch[i+1],ch[r],ch[i]);
        double b=dot(ch[i+1],ch[q],ch[i])-dot(ch[i+1],ch[p],ch[i]);
        double c=dot(ch[i+1],ch[i+1],ch[i]);
        res=min(res,a*b/c);
    }
    return res;
}

• 凸多边形最小周长外接矩形
  这个问题和最小面积外接矩形相似。 我们的目标是找到一个最小盒子（就周长而言）外接多边形 P 。

有趣的是通常情况下最小面积的和最小周长的外接矩形是重合的。 有人不禁想问这是不是总成立的。 下面的例子回答了这个问题： 多边形（灰色的）及其最小面积外接矩形（左边的）和最小周长外接矩形（右边的）。

现在， 给定一个方向， 我们可以算出 P 的端点， 以此来确定一个外接矩形。 但是， 就如同面积问题中一样， 由于有下面的结论， 我们不必检测每个状态来获得拥有最小周长的矩形：

凸多边形 P 的最小周长外接矩形存在一条边和多边形的一条边重合。

这个结论通过枚举多边形的一条重合边有力地限制了矩形的可能范围.

图示上述结论： 四条切线（红色）， 其中一条与多边形边重合， 确定了外接矩形（蓝色）。
因为与其面积问题相当， 这个问题可以通过一个基于旋转卡壳的相似的算法来解决。
下属算法的输入是顺时针顺序给定的一个凸多边形的 n 个顶点。
1. 计算全部四个多边形的端点， 称之为 xminP， xmaxP， yminP， ymaxP。
2. 通过四个点构造 P 的四条切线。 他们确定了两个“卡壳”集合。
3. 如果一条（或两条）线与一条边重合， 那么计算由四条线决定的矩形的面积， 并且保存为当前最小值。 否则将当前最小值定义为无穷大。
4. 顺时针旋转线直到其中一条和多边形的一条边重合。
5. 计算新矩形的周长， 并且和当前最小值比较。 如果小于当前最小值则更新， 并保存确定最小值的矩形信息。
6. 重复步骤4和步骤5， 直到线旋转过的角度大于90度。
7. 输出外接矩形的最小周长。
因为两对的“卡壳”确定了一个外接矩形， 这个算法考虑到了所有可能算出最小周长的矩形。 进一步， 除了初始值外， 算法的主循环只需要执行顶点总数多次。 因此算法是线性时间复杂度的。
代码和上面类似，故略。