sklearn-决策树的学习

综述

Decision Trees (DTs) 是一种用来 classification 和 regression 的无参监督学习方法。其目的是创建一种模型从数据特征中学习简单的决策规则来预测一个目标变量的值。例如，决策树通过if-then-else的决策规则来学习数据从而估测数一个正弦图像。决策树越深入，决策规则就越复杂并且对数据的拟合越好。

决策树的优势:
• 便于理解和解释。树的结构可以可视化出来。
• 训练需要的数据少。其他机器学习模型通常需要数据规范化，比如构建虚拟变量和移除缺失值,不过请注意，这种模型不支持缺失值。
• 由于训练决策树的数据点的数量导致了决策树的使用开销呈指数分布(训练树模型的时间复杂度是参与训练数据点的对数值)。
• 能够处理数值型数据和分类数据。其他的技术通常只能用来专门分析某一种变量类型的数据集。详情请参阅算法。
• 能够处理多路输出的问题。
• 使用白盒模型。如果某种给定的情况在该模型中是可以观察的，那么就可以轻易的通过布尔逻辑来解释这种情况。相比之下，在黑盒模型中的结果就是很难说明清楚。
• 可以通过数值统计测试来验证该模型。这对事解释验证该模型的可靠性成为可能。
• 即使该模型假设的结果与真实模型所提供的数据有些违反，其表现依旧良好。

决策树的缺点包括:
• 决策树模型容易过拟合。一些策略像剪枝、设置叶节点所需的最小样本数或设置数的最大深度是避免出现 该问题最为有效地方法。
• 决策树可能是不稳定的，因为数据中的微小变化可能会导致完全不同的树生成。这个问题可以通过决策树的集成来得到缓解
• 在多方面性能最优和简单化概念的要求下，学习一棵最优决策树通常是一个NP难问题。因此，实际的决策树学习算法是基于启发式算法，例如在每个节点进 行局部最优决策的贪心算法。这样的算法不能保证返回全局最优决策树。这个问题可以通过集成学习来训练多棵决策树来缓解,这多棵决策树一般通过对特征和样本有放回的随机采样来生成。
• 有些概念很难被决策树学习到,因为决策树很难清楚的表述这些概念。例如XOR，奇偶或者复用器的问题。
• 如果某些类在问题中占主导地位会使得创建的决策树有偏差。因此，我们建议在拟合前先对数据集进行平衡。

1.分类

DecisionTreeClassifier 是能够在数据集上执行多分类的类,与其他分类器一样，DecisionTreeClassifier 采用输入两个数组：数组X，用 [n_samples, n_features] 的方式来存放训练样本。整数值数组Y，用 [n_samples] 来保存训练样本的类标签。执行通过之后，可以使用该模型的predict()方法来预测样本类别；另外，也可以使用predict_proba()预测每个类的概率，这个概率是叶中相同类的训练样本的分数。
DecisionTreeClassifier 既能用于二分类（其中标签为[-1,1]）也能用于多分类（其中标签为[0,…,k-1]）。使用Lris数据集，我们可以构造一个决策树，

import numpy as np
	import matplotlib.pyplot as plt
	
	from sklearn.datasets import load_iris
	from sklearn.tree import DecisionTreeClassifier
	
	# 参数列表
	n_classes = 3
	plot_colors = "ryb"
	plot_step = 0.02
	
	# 加载数据
	iris = load_iris()
	
	for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3],
	                                [1, 2], [1, 3], [2, 3]]):
	    # 我们这里只使用两个相关的特征
	    X = iris.data[:, pair]
	    y = iris.target
	
	    # 训练模型
	    clf = DecisionTreeClassifier().fit(X, y)
	
	    # 可视化决策边界
	    plt.subplot(2, 3, pairidx + 1)
	
	    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
	    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
	    xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
	                         np.arange(y_min, y_max, plot_step))
	    plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)
	
	    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
	    Z = Z.reshape(xx.shape)
	    cs = plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlBu)
	
	    plt.xlabel(iris.feature_names[pair[0]])
	    plt.ylabel(iris.feature_names[pair[1]])
	
	    # 可视化训练点
	    for i, color in zip(range(n_classes), plot_colors):
	        idx = np.where(y == i)
	        plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
	                    cmap=plt.cm.RdYlBu, edgecolor='black', s=15)
	
	plt.suptitle("Decision surface of a decision tree using paired features")
	plt.legend(loc='lower right', borderpad=0, handletextpad=0)
	plt.axis("tight")
	plt.show()

我们可以得到如下的分类结果：

2. 回归

决策树通过使用 DecisionTreeRegressor 类也可以用来解决回归问题。如在分类设置中，拟合方法将数组X和数组y作为参数，只有在这种情况下，y数组预期才是浮点值。这里我们看一下前面的例子：

 		import numpy as np
    	from sklearn.tree import DecisionTreeRegressor #引入DecisionTreeRegressor 
    	import matplotlib.pyplot as plt
    	
    	# 创建随机的数据集
    	rng = np.random.RandomState(1)
    	X = np.sort(5 * rng.rand(80, 1), axis=0)
    	y = np.sin(X).ravel()
    	y[::5] += 3 * (0.5 - rng.rand(16))
    	
    	# 拟合回归模型，指定决策树的不同的最大深度，得到两个不同的模型
    	regr_1 = DecisionTreeRegressor(max_depth=2)
    	regr_2 = DecisionTreeRegressor(max_depth=5)
    	regr_1.fit(X, y)
    	regr_2.fit(X, y)
    	
    	# 预测某个数据
    	X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
    	y_1 = regr_1.predict(X_test)
    	y_2 = regr_2.predict(X_test)
    	
    	# 可视化
    	plt.figure()
    	plt.scatter(X, y, s=20, edgecolor="black",
    	            c="darkorange", label="data")
    	plt.plot(X_test, y_1, color="cornflowerblue",
    	         label="max_depth=2", linewidth=2)
    	plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
    	plt.xlabel("data")
    	plt.ylabel("target")
    	plt.title("Decision Tree Regression")
    	plt.legend()
    	plt.show()

我们可以得到如下的回归模型;

3. 多输出问题

一个多值输出问题是一个类似当 Y 是大小为 [n_samples, n_outputs] 的2d数组时，有多个输出值需要预测的监督学习问题。当输出值之间没有关联时，一个很简单的处理该类型的方法是建立一个n独立模型，即每个模型对应一个输出，然后使用这些模型来独立地预测n个输出中的每一个。然而，由于可能与相同输入相关的输出值本身是相关的，所以通常更好的方法是构建能够同时预测所有n个输出的单个模型。首先，因为仅仅是建立了一个模型所以训练时间会更短。第二，最终模型的泛化性能也会有所提升。对于决策树，这一策略可以很容易地用于多输出问题。 这需要以下更改：
• 在叶中存储n个输出值，而不是一个;
• 通过计算所有n个输出的平均减少量来作为划分标准.
该模块通过在 DecisionTreeClassifier和 DecisionTreeRegressor 中实现该策略来支持多输出问题。如果决策树与大小为 [n_samples, n_outputs] 的输出数组Y向匹配，则得到的估计器将:
• predict：输出n_output的值
• predict_proba：输出 n_output 数组列表
用多输出决策树进行回归分析 Multi-output Decision Tree Regression 。

4. 复杂度分析

总体来说，用来构建平衡二叉树的运行时间为

查询时间为

。尽管树的构造算法尝试生成平衡树，但它们并不总能保持平衡。假设子树能大概保持平衡，每个节点的成本包括通过

时间复杂度来搜索找到提供熵减小最大的特征。每个节点的花费为

，从而使得整个决策树的构造成本为

Scikit-learn提供了更多有效的方法来创建决策树。初始实现（如上所述）将重新计算沿着给定特征的每个新分割点的类标签直方图（用于分类）或平均值（用于回归）。与分类所有的样本特征，然后再次训练时运行标签计数，可将每个节点的复杂度降低为

，则总的成本花费为

这是一种对所有基于树的算法的改进选项。默认情况下，对于梯度提升模型该算法是打开的，一般来说它会让训练速度更快。但对于所有其他算法默认是关闭的，当训练深度很深的树时往往会减慢训练速度。

5. 实际使用技巧

• 对于拥有大量特征的数据决策树会出现过拟合的现象。获得一个合适的样本比例和特征数量十分重要，因为在高维空间中只有少量的样本的树是十分容易过拟合的。
• 考虑事先进行降维( PCA , ICA ，使您的树更好地找到具有分辨性的特征。
• 通过 export 功能可以可视化您的决策树。使用 max_depth=3 作为初始树深度，让决策树知道如何适应您的数据，然后再增加树的深度。
• 填充树的样本数量会增加树的每个附加级别。使用 max_depth 来控制输的大小防止过拟合。• 通过使用 min_samples_split 和 min_samples_leaf 来控制叶节点上的样本数量。当这个值很小时意味着生成的决策树将会过拟合，然而当这个值很大时将会不利于决策树的对样本的学习。所以尝试 min_samples_leaf=5 作为初始值。如果样本的变化量很大，可以使用浮点数作为这两个参数中的百分比。两者之间的主要区别在于 min_samples_leaf 保证叶结点中最少的采样数，而 min_samples_split 可以创建任意小的叶子，尽管在文献中 min_samples_split 更常见。
• 在训练之前平衡您的数据集，以防止决策树偏向于主导类.可以通过从每个类中抽取相等数量的样本来进行类平衡，或者优选地通过将每个类的样本权重 (sample_weight) 的和归一化为相同的值。还要注意的是，基于权重的预修剪标准 (min_weight_fraction_leaf) 对于显性类别的偏倚偏小，而不是不了解样本权重的标准，如 min_samples_leaf 。
• 如果样本被加权，则使用基于权重的预修剪标准 min_weight_fraction_leaf 来优化树结构将更容易，这确保叶节点包含样本权重的总和的至少一部分。
• 所有的决策树内部使用 np.float32 数组 ，如果训练数据不是这种格式，将会复制数据集。
• 如果输入的矩阵X为稀疏矩阵，建议您在调用fit之前将矩阵X转换为稀疏的csc_matrix ,在调用predict之前将 csr_matrix 稀疏。当特征在大多数样本中具有零值时，与密集矩阵相比，稀疏矩阵输入的训练时间可以快几个数量级。

6. DecisionTreeClassifierAPI的学习

import numpy as np 
	import pandas as pd 
	import matplotlib.pyplot as plt 
	from sklearn import datasets 
	from sklearn.preprocessing import LabelEncoder
	from sklearn import tree
	
	# ## 决策树
	#
	# paras:
	#       criterion：string，特征选择标准，可选参数，默认是gini，可以设置为entropy。gini是基尼不纯度，是将来自集合的某种结果随机应用于某一数据项的预期误差率，是一种基于统计的思想，entropy是香农熵
	#       splitter：string，特征划分点选择标准，可选参数，默认是best，可以设置为random，每个结点的选择策略。best参数是根据算法选择最佳的切分特征，例如gini、entropy。random随机的在部分划分点中找局部最优的划分点
	#                 默认的”best”适合样本量不大的时候，而如果样本数据量非常大，此时决策树构建推荐random
	
	#       max_features：int|float|string|None,划分时考虑的最大特征数，可选参数，默认是None。寻找最佳切分时考虑的最大特征数(n_features为总共的特征数)，有如下6种情况： 
	#                     如果max_features是整型的数，则考虑max_features个特征； 
	#                     如果max_features是浮点型的数，则考虑int(max_features * n_features)个特征； 
	#                     如果max_features设为auto，那么max_features = sqrt(n_features)； 
	#                     如果max_features设为sqrt，那么max_featrues = sqrt(n_features)，跟auto一样； 
	#                     如果max_features设为log2，那么max_features = log2(n_features)； 
	#                     如果max_features设为None，那么max_features = n_features，也就是所有特征都用。 
	#                     一般来说，如果样本特征数不多，比如小于50，我们用默认的”None”就可以了，如果特征数非常多，我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。
	#       max_depth：int|None,决策树最大深度，可选参数，默认是None。若为None，则节点扩展直到所有的叶子节点都是纯叶子，或者到所有叶子的数量小于min_samples_split
	#       min_samples_split：int|float,内部节点再划分所需最小样本数，可选参数，默认是2.若为整数，将min_samples_split作为最小数，若为float，min_samples_split是一个分数，且ceil(min_samples_split * n_samples)将作为每次划分时所需的最小的样本数量
	#       min_weight_fraction_leaf：float,叶子节点最小的样本权重和，可选参数，默认是0。叶节点上(所有输入样本的)权值之和的最小加权分数，当不提供sample_weight时，样本的权值相等
	#       max_leaf_nodes：int|None,最大叶子节点数，可选参数，默认是None。通过限制最大叶子节点数，可以防止过拟合
	#       class_weight：dict|list|dicts|balanced|None,类别权重，可选参数，默认是None。指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多，导致训练的决策树过于偏向这些类别。
	#                     类别的权重可以通过{class_label：weight}这样的格式给出，这里可以自己指定各个样本的权重，或者用balanced，如果使用balanced，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。
	#                     当然，如果你的样本类别分布没有明显的偏倚，则可以不管这个参数，选择默认的None。
	#       random_state：int|RandsomState instance|None,可选参数，默认是None。随机数种子。如果是整数，那么random_state会作为随机数生成器的随机数种子。随机数种子，如果没有设置随机数，随机出来的数与当前系统时间有关，每个时刻都是不同的。
	#                     如果设置了随机数种子，那么相同随机数种子，不同时刻产生的随机数也是相同的。如果是RandomState instance，那么random_state是随机数生成器。如果为None，则随机数生成器使用np.random
	#       min_impurity_split：int|float,节点划分最小不纯度,可选参数，默认是1e-7，阈值，这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝对差)小于这个阈值，则该节点不再生成子节点。即为叶子节点 
	#       presort：bool,数据是否预排序，可选参数，默认为False，这个值是布尔值，默认是False不排序。一般来说，如果样本量少或者限制了一个深度很小的决策树，设置为true可以让划分点选择更加快，决策树建立的更加快。
	#       min_samples_leaf:int|float,可选，默认为1，作为叶子节点所需的最小的样本数。只有在左分支和右分支中至少留下min_samples_leaf训练样本时，才会考虑任何深度的分割点。这可能有平滑模型的效果，特别是在回归中。
	#                        若为整数，将min_samples_split作为最小数，若为float，min_samples_split是一个分数，且ceil(min_samples_split * n_samples)将作为每次划分时所需的最小的样本数量
	#       min_impurity_decrease:float,可选，默认为0，如果这种划分导致不纯度的减少大于或等于这个值，节点将被划分，具体公式见API
	#
	# attributes:
	#       classes_:类标签(单个输出问题)，或类标签数组列表(多输出问题)。
	#       max_features_:max_features的推断值
	#       n_classes_:类的数量(对于单个输出问题)，或包含每个输出的类的数量的列表(对于多输出问题)。
	#       n_features_:执行fit时的特征数量
	#       n_outputs_:执行fit时的输出的数量
	#       tree_:底层树对象
	#
	# methods:
	#       apply(X[, check_input]):返回每个样本预测为的叶子的索引
	#       decision_path(X[, check_input]):返回树中的决策路径
	#       fit(X, y[, sample_weight, check_input, …]):从训练集(X, y)构建决策树分类器
	#       get_params([deep]):获取此估计器的参数
	#       predict(X[, check_input]):预测X的类或回归值
	#       predict_log_proba(X):预测输入样本X的类对数概率
	#       predict_proba(X[, check_input]):预测输入样本X的类概率
	#       score(X, y[, sample_weight]):Returns the mean accuracy on the given test data and labels
	#       set_params(**params):设置该估计器的参数
	
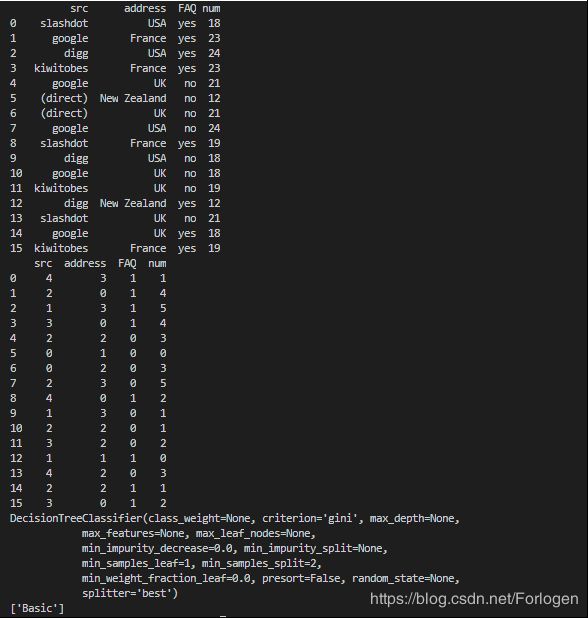
	# 下面的数据分为为每个用户的来源网站、位置、是否阅读FAQ、浏览网页数目、选择的服务类型（目标结果）
	attr_arr=[['slashdot','USA','yes',18,'None'],
	         ['google','France','yes',23,'Premium'],
	         ['digg','USA','yes',24,'Basic'],
	         ['kiwitobes','France','yes',23,'Basic'],
	         ['google','UK','no',21,'Premium'],
	         ['(direct)','New Zealand','no',12,'None'],
	         ['(direct)','UK','no',21,'Basic'],
	         ['google','USA','no',24,'Premium'],
	         ['slashdot','France','yes',19,'None'],
	         ['digg','USA','no',18,'None'],
	         ['google','UK','no',18,'None'],
	         ['kiwitobes','UK','no',19,'None'],
	         ['digg','New Zealand','yes',12,'Basic'],
	         ['slashdot','UK','no',21,'None'],
	         ['google','UK','yes',18,'Basic'],
	         ['kiwitobes','France','yes',19,'Basic']]
	
	#生成属性数据集和结果数据集
	dataMat = np.mat(attr_arr)
	arrMat = dataMat[:,0:4]
	resultMat = dataMat[:,4]
	
	# 构造数据集成pandas结构，为了能理解属性的名称
	attr_names = ['src', 'address', 'FAQ', 'num']   #特征属性的名称
	attr_pd = pd.DataFrame(data=arrMat,columns=attr_names)    #每行为一个对象，每列为一种属性，最后一个为结果值
	print(attr_pd)
	
	#将数据集中的字符串转化为代表类别的数字。因为sklearn的决策树只识别数字
	le = LabelEncoder()
	for col in attr_pd.columns:                                            #为每一列序列化,就是将每种字符串转化为对应的数字。用数字代表类别
	    attr_pd[col] = le.fit_transform(attr_pd[col])
	print(attr_pd)
	
	# 构建决策树
	clf = tree.DecisionTreeClassifier()
	clf.fit(attr_pd, resultMat)
	print(clf)
	
	# 使用决策树进行预测
	result = clf.predict([[1,1,1,0]])    # 输入也必须是数字的。分别代表了每个数字所代表的属性的字符串值
	print(result)
	
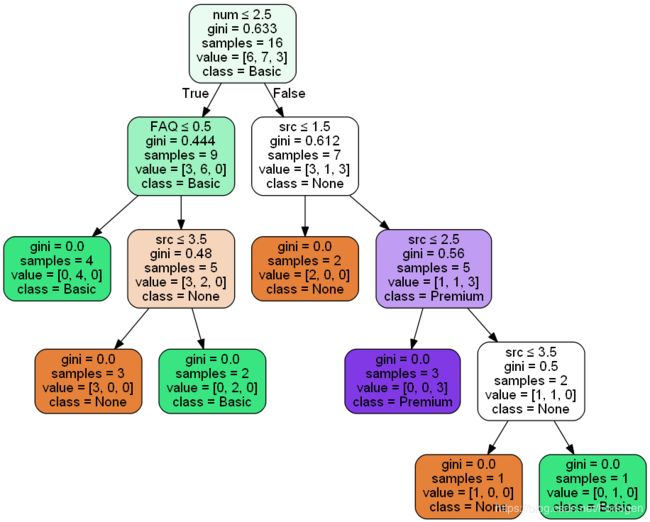
	# 将决策树保存成图片
	from sklearn.externals.six import StringIO
	import pydotplus
	
	dot_data = StringIO()
	target_name=['None','Basic','Premium']
	tree.export_graphviz(clf, out_file=dot_data,feature_names=attr_names,
	                     class_names=target_name,filled=True,rounded=True,
	                     special_characters=True)
	graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
	graph.write_png('tree.png')

结果：

决策树其他API的使用类似，这里就不写了。
skleanr中文文档-决策树
sklearn-tree
python机器学习库sklearn——决策树

7. 决策树算法：ID3、C4.5、C5.0、CART

在实际使用中常用的决策树的算法有ID3、C4.5、C5.0、CART这么几个。

ID3(Iterative Dichotomiser 3)是1986年由Ross Quinlan提出。该算法创建一个多路树，为每个节点(即以贪婪的方式)找到分类特征，从而为分类目标获得最大的信息增益。树生长到最大尺寸，然后通常使用修剪步骤来提高树对未知数据的泛化能力。

C4.5是ID3的继承者，它通过动态定义一个离散属性(基于数值变量)，将连续属性值划分为一组离散的区间，从而消除了特性必须分类的限制。C4.5将训练好的树(即ID3算法的输出)转换为if-then规则集。然后评估每个规则的准确性，以确定应用规则的顺序。剪枝是通过删除规则的先决条件来完成的，前提是如果没有规则，规则的准确性就会提高。

C5.0是Quinlan最新提出的算法，相比于C4.5，他使用的内存更小，构建的规则集更小，同时准确性更高。

CART(分类和回归树)与C4.5非常相似，但不同之处在于它支持数值目标变量(回归)，并且不计算规集。CART使用在每个节点上产生最大信息增益的特性和阈值构造二叉树。scikit-learn使用了CART算法的优化版本;然而，scikit-learn实现目前还不支持分类变量。

8. 决策树算法中的数学公式

假设训练数据为Xi∈R^n，R维n维向量，I = 1,2,…，标签向量y∈R^l。表示有l个类别，决策树递归的根据某些标准划分空间，以便将具有相同标签的样本分组在一起。

假设节点m用Q表示，对于每一个节点根据θ = (j,tm)进行划分，j表示第j个特征，tm表示阈值，根据它将数据划分为Qleft(θ)和Qright(θ)两个子集

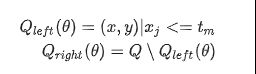
m处的不纯度使用函数H()计算，不同的计算不纯度的函数取决于要处理的问题，是分类还是回归

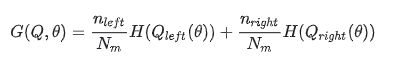
选择是的不纯度最小的那些参数组合

不断的循环计算参数Qleft(θ*)和Qright(θ*)，直到到达所设置的树的最大深度、叶子节点所拥有的最小的样本量或是是纯叶子节点。

对于分类问题来说，若目标为节点m的分类结果，取值为0,1，…，K-1，Nm个观测值可能有Rm种结果，我们设

表示K类观测值在总样本点m的比例。
常用的用来衡量不纯度的标准有基尼系数、熵、误分率，公式分别如下所示：其中X表示节点m的训练数据

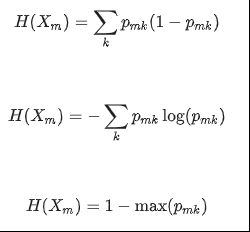
对于回归问题来说，如果目标是一个连续的值,然后对节点m，通常使用均方误差（Mean Squared Error）作为划分的标准，在最终的节点上使用均值来最小化L2误差，对于Mean Absolute Error来说，使用终端节点的中值最小化L1误差。

Mean Squared Error的表达式如下所示：

Mean Absolute Error的表达式如下所示：

同样Xm表示节点m的训练数据

References:

• https://en.wikipedia.org/wiki/Decision_tree_learning
• https://en.wikipedia.org/wiki/Predictive_analytics
• L. Breiman, J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984.
• J.R. Quinlan. C4. 5: programs for machine learning. Morgan Kaufmann, 1993.
• T. Hastie, R. Tibshirani and J. Friedman. Elements of Statistical Learning, Springer, 2009.