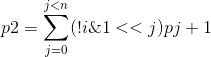期望与概率DP专题/高斯消元
高斯消元
总结:概率和期望问题的求解都要依靠递推式,概率问题按照递推式进行dp,期望问题根据递推式化简的难易程度通过化简再dp或高斯消元求解,该类问题大部分仍属于各个类型的dp求解问题
2018.9.3-概率与期望dp学习
Discovering Gold
一排1到n的格子,每个格子上有黄金 ai ,你最开始在 1 号,每一次投骰子决定到哪一个格子,超出1~n范围则重新投掷,你到了哪个格子就得到哪个格子的金币,问最终在n 能得到金币的期望
#include
#include
const int MAX=1e2+5;
int a[MAX];
double dp[MAX];
int t,n;
int main()
{
scanf("%d",&t);
for(int tc=1;tc<=t;++tc)
{
memset(dp,0,sizeof(dp));
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
dp[1]=1.0;
for(int i=1;in) tmp=n-i;
dp[i+j]+=dp[i]/tmp;
}
}
double ans=0;
for(int i=1;i<=n;++i) ans+=dp[i]*a[i];
printf("Case %d: %f\n",tc,ans);
}
return 0;
} HDU3366 Passage
有n扇门和m枚金币,每扇门后有3种可能:1.出路概率p,2.另一扇门概率1-p-q,3.失去一枚金币并且出现另一扇门概率q,门可选择,求在最优选择情况下找到出路得概率
根据p/q从大到小对每扇门排序即为最优策略,注意q可能的值为0,需eps处理
#include
#include
#include
using namespace std;
const int MAX=1e3+5;
const double eps=1e-16;
double dp[MAX][15],ans;
int t,n,m;
struct P
{
double p,q;
}a[MAX];
inline bool cmp(P& x,P& y)
{
return (x.p+eps)/(x.q+eps)>(y.p+eps)/(y.q+eps);
}
int main()
{
scanf("%d",&t);
for(int tc=1;tc<=t;++tc)
{
memset(dp,0,sizeof(dp));
scanf("%d%d",&n,&m);
for(int i=0;i=0;--j)
{
ans+=dp[i][j]*a[i].p;
if(i=1)dp[i+1][j-1]+=dp[i][j]*a[i].q;
if(i Island of Survival
小岛上有man\tiger\deer三种生物,每天都有两种相遇:1.tiger-man 2.tiger-tiger 3.tiger-deer 4.man-deer/deer 5.deer-deer
求man活下来的概率,当且仅当tiger==0。:本题求的是man能活下来的最终概率而不是某种情况下仍存活的概率,题中3\4\5种情况只能延长man的存活时间,而不能影响man的存活概率,因此只需要对1\2情况进行讨论。
#include
#include
const int MAX=1e3+5;
double dp[MAX];
int t,n,m;
int main()
{
scanf("%d",&t);
for(int tc=1;tc<=t;++tc)
{
memset(dp,0,sizeof(dp));
scanf("%d%d",&n,&m);
if(n==0) {printf("Case %d: 1\n",tc);continue;}
if(n%2==1) {printf("Case %d: 0\n",tc);continue;}
dp[n]=1;
for(int i=n;i>=2;i-=2) dp[i-2]=dp[i]*(i-1)/(i+1);
printf("Case %d: %.6f\n",tc,dp[0]);
}
return 0;
}
Bag of mice
有n只白鼠m只黑鼠,小D和小P二人随机各抓1只并且小D先手,小P抓完后会有1只小鼠出逃,求小D先抓到白鼠的概率
与上题相似,抓到白鼠则游戏结束,只需讨论2人都抓不到的概率和2种小鼠随机出逃的概率,答案为各种情况下抓到白鼠的概率之和: 本题我的解法中用eps忽略不会到达的情况,需要注意eps精度的设置,题中精度偏差不超过1e-9,eps=1e-11可AC
#include
#include
#include
using namespace std;
const int MAX=1e3+1;
const double eps=1e-11;
double dp[MAX][MAX];
int n,m;
int main()
{
scanf("%d%d",&n,&m);
memset(dp,0,sizeof(dp));
dp[n][m]=1;
double ans=0,tmp;
for(int i=n;i>0;--i)
{
for(int j=m;j>=0;--j)
{
if(dp[i][j]=2)tmp=dp[i][j]*j*(j-1)/(i+j)/(i+j-1);
if(i>=1&&j>=2)dp[i-1][j-2]+=tmp*i/(i+j-2);
if(j>=3)dp[i][j-3]+=tmp*(j-2)/(i+j-2);
}
}
printf("%.9f\n",ans);
return 0;
}
Scout YYF I
一维路径上有N个地雷,有2种情况:1.走一步概率p,2.走两步概率1-p,求从1走到MAX不踩到雷得概率(n<=10,MAX=1e8)
把地雷看作区间间断点,假设 ![]() 为间断点
为间断点![]() ,走两步到达,进行区间概率统计即可
,走两步到达,进行区间概率统计即可
#include
#include
#include
using namespace std;
int a[11],n;
double p,q;
struct Mat
{
double m[2][2];
Mat(){memset(m,0,sizeof(m));}
inline void init()
{
m[0][0]=0;m[0][1]=1;m[1][0]=q;m[1][1]=p;
}
};
inline Mat multi(const Mat &a,const Mat &b)
{
Mat c;
for(int i=0;i<2;++i)
for(int j=0;j<2;++j)
for(int k=0;k<2;++k)
c.m[i][j]+=a.m[i][k]*b.m[k][j];
return c;
}
Mat pow(Mat &a,int k)
{
Mat b;
for(int i=0;i<2;++i) b.m[i][i]=1;
while(k)
{
if(k&1) b=multi(b,a);
a=multi(a,a);
k>>=1;
}
return b;
}
double ans;
int main()
{
while(~scanf("%d%lf",&n,&p))
{
q=1.0-p;
for(int i=0;i Batting Practice
每次投1个球投不中概率为p,连中n球或连失m球则停止,求投球次数的期望
关键词:马尔可夫链、正向推概率反向推期望
![]()
![]()
![]()
设![]() ,
,![]() ,
,![]()
1. ![]()
#include
#include
#include
using namespace std;
const int MAX=51;
const double eps=1e-8;
int t,n,m;
double p,q;
int main()
{
scanf("%d",&t);
for(int tc=1;tc<=t;++tc)
{
scanf("%lf%d%d",&p,&n,&m);
q=1.0-p;
if(p ZOJ 3329 One Person Game
有三个骰子,分别有K1,K2,K3个面,点数都在[1,K1]\[1,K2]\[1,K3]之间,同时掷出三个骰子:若点数分别为a,b,c则sum=0;否则sum+=点数之和,当sum>n结束,求掷骰子次数的期望
同上,概率公式中有环,每一个![]() 都可以转化到
都可以转化到![]() ,不妨设
,不妨设![]() 代入迭代化简得
代入迭代化简得
问题化简为求![]() 和
和![]()
#include
#include
#include
using namespace std;
const int MAX=5e2+1;
const double eps=1e-8;
double p[MAX],pa[MAX],pb[MAX],p0;
int t,n,K1,K2,K3,a,b,c;
int main()
{
scanf("%d",&t);
while(t--)
{
memset(p,0,sizeof(p));
memset(pa,0,sizeof(pa));
memset(pb,0,sizeof(pb));
scanf("%d%d%d%d%d%d%d",&n,&K1,&K2,&K3,&a,&b,&c);
p0=1.0/K1/K2/K3;
for(int i=1;i<=K1;++i)
for(int j=1;j<=K2;++j)
for(int k=1;k<=K3;++k)
p[i+j+k]+=p0;
p[a+b+c]-=p0;
for(int i=n;i>=0;--i)
{
pa[i]+=p0;
pb[i]+=1;
for(int j=3;j<=K1+K2+K3&&i+j<=n;++j)
{
pa[i]+=pa[i+j]*p[j];
pb[i]+=pb[i+j]*p[j];
}
}
printf("%.8f\n",pb[0]/(1.0-pa[0]));
}
return 0;
}
HDU 4336 Card Collector
买魔法士干脆面收集袋中卡牌,共有n张卡牌,袋中有i卡牌得概率为pi,![]() ,求买干脆面的期望
,求买干脆面的期望
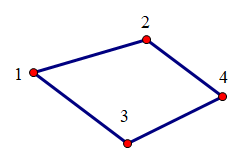
n张卡牌形成1< 根据递推式反向求期望 HDU4870 Rating 有两个账号,每次选取一个分数最低的账号进行游戏,有p得概率得1分,1-p得概率失2分,最低0分,求1个号到达20的期望 由题意得,两个号的分差必定不超过1,当一个号为20分时,另一个为19 按递推式建立矩阵,套用高斯消元函数,得到解集 该题的递推式也可以通过换元 ZJUT 1423 地下迷宫 ZJUT 1317 掷飞盘 HDU 4418 Time travel 转载 对离散型随机变量x,其概率为p,有 对随机变量A、B,有 第二条式子是今天的主角,他表明了期望有线性的性质,简单理解就是期望之间可根据关系,简单运算(不严谨的理解)。 这就为我们解决一个期望问题,不断转化为解决另外的期望问题,最终转化到一个已知的期望上。 举一个求期望最简单的例子,见下图。 假设有个人在 1号节点处,每一分钟他会缘着边随机走到一个节点或者在原地停留,问他走到4号节点需要平均几分钟? 这是个简单的期望问题,我们用Ei(i=1,2,3,4) 表示从i号节点走到4号节点的数学期望值。根据题意对1号节点有 E1=(1/3)*E1+(1/3)*E2+(1/3)*E3+1 ① 表示 他下一分钟可以走到2或者3或在原地1,每个可能概率是1/3 ,注意是下一分钟,故要加上1. 同理我们对节点2,3同样可以列出 E2=(1/3)*E1+(1/3)*E2+(1/3)*E4+1 ② E3=(1/3)*E1+(1/3)*E3+(1/3)*E4+1 ③ 那E4等于多少呢? 很明显E4=0 ④,因为他就是要到点4 这样上面1234式其实就是组成了一组方程组,解方程组就可得出E1!!,用高斯消元,复杂度是O(n^3) 从上述例子,我们可总结出如何解决期望类问题,根据题意,表示出各个状态的期望(上例的Ei,1234),根据概率公式,列出期望之间的方程,解方程即可。 下面看用上述思路如何解决一道题(poj2096) 题意简述: 一个人受雇于某公司要找出某个软件的bugs和subcomponents,这个软件一共有n个bugs和s个subcomponents,每次他都能同时随机发现1个bug和1个subcomponent,问他找到所有的bugs和subcomponents的期望次数。 我们用E(i,j)表示他找到了i个bugs和j个subcomponents,离找到n个bugs和s个subcomponents还需要的期望次数,这样要求的就是E(0,0),而E(n,s)=0,对任意的E(i,j),1次查找4种情况,没发现任何新的bugs和subcomponents,发现一个新的bug,发现一个新的subcomponent,同时发现一个新的bug和subcomponent,用概率公式可得: E(i,j)=1+(i*j/n/s)*E(i,j)+(i*(s-j)/n/s)E(i,j+1)+((n-i)*j/n/s)*E(i+1,j)+(n-i)*(s-j)/n/s*E(i+1,j+1); 这样根据边界就可解出所有的E(i,j),注意因为当我们找到n个bugs和s个subcomponents就结束,对i>n||j>s均无解的情况,并非期望是0.(数学上常见问题,0和不存在的区别) 那这题是否也是要用高斯消元呢? 用高斯消元得话复杂度是O(n^3),达到10^18 根本是不可解的!! 但其实,注意观察方程,当我们要解E(i,j)的话就需要E(i+1,j),E(I,j+1),E(i+1,j+1), 一开始已知E(n,s),那其实只要我们从高往低一个个解出I,j就可以了! 即可根据递推式解出所有的E(I,j) 复杂度是O(n),10^6 ,完美解决。 从上面这道题,我们再次看到了解决期望问题的思路,而且是用到了递推解决问题,其实可递推的原因,当我们把各个状态当成是一个个节点时,概率关系为有向边,我们可看到,可递推的问题其实就是这个关系图是无环的!!那必须要用方程组解决的问题其实就是存在环!!!! 而且我还要指出的是用高斯消元的时候,要注意误差的问题,最好把式子适当的增大,避免解小数,否则误差太大,估计也会卡题。 《信息学竞赛中概率问题求解初探》 《浅析竞赛中一类数学期望问题的解决方法》 《有关概率和期望问题的研究 》![]()
#include高斯消元
![]()
![]()
![]() 表示从i分到20分的期望,所以答案即为
表示从i分到20分的期望,所以答案即为![]() :两倍的0~20减去19~20
:两倍的0~20减去19~20![]() 进行化简
进行化简#include![]()
![]()
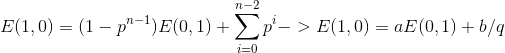


![a[i]=\sum_{x=3}^{K1+K2+K3}a[i+x]+p0](http://img.e-com-net.com/image/info8/58193e51bfd3491ea73b77c20981c892.gif)
![b[i]=\sum_{x=3}^{K1+K2+K3}b[i+x]+1](http://img.e-com-net.com/image/info8/71764bd5384d460398c0c3f962925396.gif)
![E[i]=E[i]*ps+\sum_{j=0}^{j<n}(i\&1<<j)E[i]*pj+\sum_{j=0}^{j<n}(!i\&1<<j)E[i]*pj+1](http://img.e-com-net.com/image/info8/0db81829279043bc8be90ff307f2a3ab.gif)