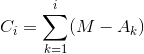七夕祭(贪心+分金币问题)
问题 M: 七夕祭
时间限制: 1 Sec 内存限制: 128 MB
提交: 75 解决: 20
[提交] [状态] [讨论版] [命题人:admin]
题目描述
七夕节因牛郎织女的传说而被扣上了「情人节」的帽子。于是TYVJ今年举办了一次线下七夕祭。Vani同学今年成功邀请到了cl同学陪他来共度七夕,于是他们决定去TYVJ七夕祭游玩。
TYVJ七夕祭和11区的夏祭的形式很像。矩形的祭典会场由N排M列共计N×M个摊点组成。虽然摊点种类繁多,不过cl只对其中的一部分摊点感兴趣,比如章鱼烧、苹果糖、棉花糖、射的屋……什么的。Vani预先联系了七夕祭的负责人zhq,希望能够通过恰当地布置会场,使得各行中cl感兴趣的摊点数一样多,并且各列中cl感兴趣的摊点数也一样多。不过zhq告诉Vani,摊点已经布置完毕了,唯一的调整方式就是交换两个相邻的摊点。两个摊点相邻,当且仅当他们处在同一行或者同一列的相邻位置上。由于zhq率领的TYVJ开发小组成功地扭曲了空间,每一行或每一列的第一个位置和最后一个位置也算作相邻。现在Vani想知道他的两个要求最多能满足多少个。在此前提下,至少需要交换多少次摊点。
输入
第一行包含三个整数N和M和T。T表示cl对多少个摊点感兴趣。
接下来T行,每行两个整数x,y,表示cl对处在第x行第y列的摊点感兴趣。
输出
首先输出一个字符串。如果能满足 Vani 的全部两个要求,输出 both;如果通过调整 只能使得各行中 cl 感兴趣的摊点数一样多,输出 row;如果只能使各列中 cl 感兴趣的摊点 数一样多,输出 column;如果均不能满足,输出 impossible。
如果输出的字符串不是 impossible, 接下来输出最小交换次数,与字符串之间用一 个空格隔开。
样例输入
2 3 4 1 3 2 1 2 2 2 3
样例输出
row 1
提示
对于30%的数据,N,M≤100。
对于70%的数据,N,M≤1000。
对于100%的数据,1≤N,M≤100000,0≤T≤min(NM,100000),1≤x≤N,1≤y≤M。
分析:这个题是均分纸牌,分金币的升级版。下面以分金币问题引入。
一、分金币:
1、题意:圆桌旁坐着n个人,每人有一定数量的金币,金币总数总能被n整除。每个人可以给他左右相邻的人一些金币,最终使得每个人的金币数相等,你的任务是求出被转手的金币数量的最小值。
2、已知每个人初始情况下手中的金币数,那么总金币数MZ=X1+X2+X3+....+XN。最终每个人获得的金币就是M=MZ/N。
3、设整个交换过程中第n个人给第n-1个人共An枚金币,对于n=1时为第一人给第n个人金币数。
4、可得
x1-A1+A2=M; => A1=x1+A2-M;
x2-A2+A3=M; => A2=x2+A3-M;
x3-A3+A4=M; => A3=x3+A4-M;
x4-A4+A1=M; => A4=x4+A1-M;
5、X2=X1-(M-A1);
X3=X2-(M-A2);
X4=X3-(M-A3);
X5=X4-(M-A4);
x2=x1-C1;
x3=x1-C2;
x4=X1-C3;
被转手的金币数量:ans=|x1|+|x2|+|x3|+|x4|........+|xn|=|x1-0|+|x1-C1|+|x1-C2|.....+|x1-Cn-1|。
(看不懂的,可以从4开始自己往6推一下)
7、问题就是就一个ans的最小值,就可以看作,一共n个点,找到一个点到其它各个点的距离之和最小,经典的货仓选址问题。
X1为C数组的中位数时ans最小。到这里就搞定了。
二、七夕祭
1、impossible的情况很简单,就是行数、列数都不是T的因数。
2、对于行和列互不影响,分开求,就是两个分金币问题。
3、如果n是T的因数,m也是T的因数,那么就是both。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include