机器学习数据、特征处理、模型融合
一 解决问题流程:
o 了解场景和目标
o 了解评估准则
o 认识数据
o 数据预处理(清洗,调权)
o 特征工程
o 模型调参
o 模型状态分析
o 模型融合
二 数据预处理
(1) 数据清洗
a: 不可信的样本丢掉
b: 缺省值极多的字段考虑不用
(2) 数据采样
a:下/上采样
b:保证样本均衡
三 特征工程
1 特征处理
(1) 数值型
(2) 类别型
(3)时间类
(4)文本型
(5)统计型
(6)组合特征
(1) 数值型:处理方式如下
a: 幅度调整/归一化 幅度调整到[0,1]范围内
b: 统计值max, min, mean, std
c: 离散化
d: Hash分桶
e: 每个类别下对应的变量统计值histogram(分布状况)
f: 试试 数值型 => 类别型
(2) 类别型:处理方式如下
a: one-hot编码/ 哑变量 pd.get_dummies()
b: Hash与聚类处理
c: 小技巧:统计每个类别变量下各个target比例,转成数值型
(3)时间类:处理方式如下
既可以看做连续值,也可以看做离散值
连续值
a) 持续时间(单页浏览时长)
b) 间隔时间(上次购买/点击离现在的时间)
离散值
a) 一天中哪个时间段(hour_0-23)
b) 一周中星期几(week_monday...)
c) 一年中哪个星期
d) 一年中哪个季度
e) 工作日/周末
(4)文本型
a: 词袋
文本数据预处理后,去掉停用词,剩下的词组成的list,在词库中的映射稀疏向量。
b: 使用Tf–idf 特征
TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成 反比下降。
(5)统计型
a: 加减平均:商品价格高于平均价格多少,用户在某个品类下消费超过平均用户多少,用户连续登录天数超过平均多少...
b: 分位线:商品属于售出商品价格的多少分位线处
c: 次序型:排在第几位
d: 比例类:电商中,好/中/差评比例,你已超过全国百分之…的同学
(6)组合特征
a: 简单组合特征:拼接型
user_id&&category: 10001&&女裙 10002&&男士牛仔
user_id&&style: 10001&&蕾丝 10002&&全棉
b: 模型特征组合
用GBDT产出特征组合路径
组合特征和原始特征一起放进LR训练
最早Facebook使用的方式,多家互联网公司在用
2 特征选择
(1)原因:
冗余:部分特征的相关度太高了,消耗计算性能。
噪声:部分特征是对预测结果有负影响
(2)特征选择 VS 降维
前者只踢掉原本特征里和结果预测关系不大的,后者做特征的计算组合构成新特征.
SVD或者PCA确实也能解决一定的高维度问题
(3)常见特征选择方式
过滤型、包裹型、嵌入型
a: 过滤型
评估单个特征和结果值之间的相关程度,排序留下Top相关的特征部分。
Pearson相关系数,互信息,距离相关度
缺点:没有考虑到特征之间的关联作用,可能把有用的关联特征误踢掉。
b:包裹型
把特征选择看做一个特征子集搜索问题,筛选各种特征子集,用模型评估效果。
典型的包裹型算法为 “递归特征删除算法”(recursive feature elimination algorithm)
比如用逻辑回归,怎么做这个事情呢?
① 用全量特征跑一个模型
② 根据线性模型的系数(体现相关性),删掉5-10%的弱特征,观察准确率/auc的变化
③ 逐步进行,直至准确率/auc出现大的下滑停止
c:嵌入型
根据模型来分析特征的重要性(有别于上面的方式,是从生产的模型权重等)。
最常见的方式为用正则化方式来做特征选择。
举个例子,最早在电商用LR做CTR预估,在3-5亿维的系数特征上用L1正则化的LR模型。剩余2-3千万的feature,意味着其它的feature重要度不够。
模型融合方法:
1 Voting
模型融合其实也没有想象的那么高大上,从最简单的Voting说起,这也可以说是一种模型融合。假设对于一个二分类问题,有3个基础模型,那么就采取投票制的方法,投票多者确定为最终的分类。
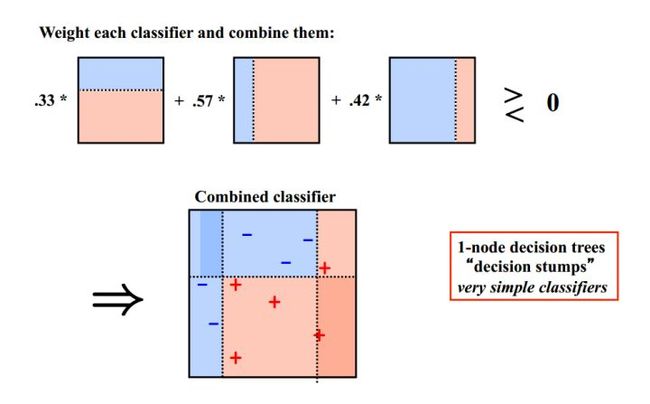
2 Averaging
对于回归问题,一个简单直接的思路是取平均。稍稍改进的方法是进行加权平均。权值可以用排序的方法确定,举个例子,比如A、B、C三种基本模型,模型效果进行排名,假设排名分别是1,2,3,那么给这三个模型赋予的权值分别是3/6、2/6、1/6
这两种方法看似简单,其实后面的高级算法也可以说是基于此而产生的,Bagging或者Boosting都是一种把许多弱分类器这样融合成强分类器的思想。
3 Bagging
Bagging就是采用有放回的方式进行抽样,用抽样的样本建立子模型,对子模型进行训练,这个过程重复多次,最后进行融合。大概分为这样两步:
- 重复K次
- 有放回地重复抽样建模
- 训练子模型
2.模型融合
- 分类问题:voting
- 回归问题:average
Bagging算法不用我们自己实现,随机森林就是基于Bagging算法的一个典型例子,采用的基分类器是决策树。R和python都集成好了,直接调用。
4 Boosting
Bagging算法可以并行处理,而Boosting的思想是一种迭代的方法,每一次训练的时候都更加关心分类错误的样例,给这些分类错误的样例增加更大的权重,下一次迭代的目标就是能够更容易辨别出上一轮分类错误的样例。最终将这些弱分类器进行加权相加。引用加州大学欧文分校Alex Ihler教授的两页PPT
同样地,基于Boosting思想的有AdaBoost、GBDT等,在R和python也都是集成好了直接调用。
PS:理解了这两点,面试的时候关于Bagging、Boosting的区别就可以说上来一些,问Randomfroest和AdaBoost的区别也可以从这方面入手回答。也算是留一个小问题,随机森林、Adaboost、GBDT、XGBoost的区别是什么?
5 Stacking
Stacking方法其实弄懂之后应该是比Boosting要简单的,毕竟小几十行代码可以写出一个Stacking算法。我先从一种“错误”但是容易懂的Stacking方法讲起。
Stacking模型本质上是一种分层的结构,这里简单起见,只分析二级Stacking.假设我们有3个基模型M1、M2、M3。
1. 基模型M1,对训练集train训练,然后用于预测train和test的标签列,分别是P1,T1
对于M2和M3,重复相同的工作,这样也得到P2,T2,P3,T3。
2. 分别把P1,P2,P3以及T1,T2,T3合并,得到一个新的训练集和测试集train2,test2.
3. 再用第二层的模型M4训练train2,预测test2,得到最终的标签列。
Stacking本质上就是这么直接的思路,但是这样肯定是不行的,问题在于P1的得到是有问题的,用整个训练集训练的模型反过来去预测训练集的标签,毫无疑问过拟合是非常非常严重的,因此现在的问题变成了如何在解决过拟合的前提下得到P1、P2、P3,这就变成了熟悉的节奏——K折交叉验证。我们以2折交叉验证得到P1为例,假设训练集为4行3列
将其划分为2部分
用traina训练模型M1,然后在trainb上进行预测得到preb3和pred4
在trainb上训练模型M1,然后在traina上进行预测得到pred1和pred2
然后把两个预测集进行拼接
对于测试集T1的得到,有两种方法。注意到刚刚是2折交叉验证,M1相当于训练了2次,所以一种方法是每一次训练M1,可以直接对整个test进行预测,这样2折交叉验证后测试集相当于预测了2次,然后对这两列求平均得到T1。
或者直接对测试集只用M1预测一次直接得到T1。
P1、T1得到之后,P2、T2、P3、T3也就是同样的方法。理解了2折交叉验证,对于K折的情况也就理解也就非常顺利了。所以最终的代码是两层循环,第一层循环控制基模型的数目,每一个基模型要这样去得到P1,T1,第二层循环控制的是交叉验证的次数K,对每一个基模型,会训练K次最后拼接得到P1,取平均得到T1。这下再把@Wille博文中的那张图片放出来就很容易看懂了。
![]()
该图是一个基模型得到P1和T1的过程,采用的是5折交叉验证,所以循环了5次,拼接得到P1,测试集预测了5次,取平均得到T1。而这仅仅只是第二层输入的一列/一个特征,并不是整个训练集。再分析作者的代码也就很清楚了。也就是刚刚提到的两层循环。
以上是理论上的讲解,下面通过一个例子来讲解
本文以Kaggle的Titanic(泰坦尼克预测)入门比赛来讲解stacking的应用(两层!)。
数据的行数:train.csv有890行,也就是890个人,test.csv有418行(418个人)。
而数据的列数就看你保留了多少个feature了(通过特征工程预处理),因人而异。这里train保留了 7+1(1是预测列)。
在网上为数不多的stacking内容里,相信你早看过了这张图: 
因为这张图极具‘误导性’。
把图改了一下: 
别找不同了,就是最上面 Model2,3,4,5 改成了 Model1,1,1,1
对于每一轮的 5-fold,Model 1都要做满5次的训练和预测。
Titanic 栗子:
Train Data有890行。(请对应图中的上层部分)
每1次的fold,都会生成 713行 小train, 178行 小test。我们用Model 1来训练 713行的小train,然后预测 178行 小test。预测的结果是长度为 178 的预测值。
这样的动作走5次! 长度为178 的预测值 X 5 = 890 预测值,刚好和Train data长度吻合。这个890预测值是Model 1产生的,我们先存着,因为,一会让它将是第二层模型的训练来源。
重点:这一步产生的预测值我们可以转成 890 X 1 (890 行,1列),记作 P1 (大写P)
接着说 Test Data 有 418 行。(请对应图中的下层部分,对对对,绿绿的那些框框)
每1次的fold,713行 小train训练出来的Model 1要去预测我们全部的Test Data(全部!因为Test Data没有加入5-fold,所以每次都是全部!)。此时,Model 1的预测结果是长度为418的预测值。
这样的动作走5次!我们可以得到一个 5 X 418 的预测值矩阵。然后我们根据行来就平均值,最后得到一个 1 X 418 的平均预测值。
重点:这一步产生的预测值我们可以转成 418 X 1 (418行,1列),记作 p1 (小写p)
走到这里,你的第一层的Model 1完成了它的使命。
第一层还会有其他Model的,比如 Model 2,同样的走一遍, 我们有可以得到 890 X 1 (P2) 和 418 X 1 (p2) 列预测值。
这样吧,假设你第一层有3个模型,这样你就会得到:
来自5-fold的预测值矩阵 890 X 3,(P1,P2, P3) 和 来自Test Data预测值矩阵 418 X 3, (p1, p2, p3)。
到第二层了………………
来自5-fold的预测值矩阵 890 X 3 作为你的Train Data,训练第二层的模型
来自Test Data预测值矩阵 418 X 3 就是你的Test Data,用训练好的模型来预测他们吧。
stack方法Python实现
具体例子可参考这篇博客:博客
from sklearn.model_selection import KFold
# Some useful parameters which will come in handy later on
ntrain = train.shape[0]
ntest = test.shape[0]
SEED = 0 # for reproducibility
NFOLDS = 5 # set folds for out-of-fold prediction
kf = KFold(n_splits=NFOLDS, random_state=SEED, shuffle=False)
def get_oof(clf, x_train, y_train, x_test):
oof_train = np.zeros((ntrain,))
oof_test = np.zeros((ntest,))
oof_test_skf = np.empty((NFOLDS, ntest)) #NFOLDS行,ntest列的二维array
for i, (train_index, test_index) in enumerate(kf.split(x_train)): #循环NFOLDS次
x_tr = x_train[train_index]
y_tr = y_train[train_index]
x_te = x_train[test_index]
clf.fit(x_tr, y_tr)
oof_train[test_index] = clf.predict(x_te)
oof_test_skf[i, :] = clf.predict(x_test) #固定行填充,循环一次,填充一行
oof_test[:] = oof_test_skf.mean(axis=0) #axis=0,按列求平均,最后保留一行
return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1) #转置,从一行变为一列参考文献:
1 https://blog.csdn.net/u013395516/article/details/79745063?utm_source=blogxgwz10
2 https://zhuanlan.zhihu.com/p/25836678
3 https://blog.csdn.net/Koala_Tree/article/details/78725881