八数码问题 BFS+A* 到N数码问题
八数码问题
在3×3的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字。棋盘中留有一个空格,空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
【参考博客】:
7种方法求解八数码问题。参考了其最后一种方法,即BFS+A*,但他的c++代码没法运行(这可能与我用的c++11有关,好多输入输出提示不安全,而且他代码里面有好多的从字符串到数字之间的来回转换,各种倒腾),看懂思想和代码后,本人进行了重构,使用python3。
【分析】:
每移动一次空格,就产生一种状态。使用BFS来搜索,但这里使用优先队列而不是普通的队列,这样就可以利用A*算法的核心——评估函数f(n)=g(n)+h(n),对每一种状态用评估函数进行优先队列的排序(只要你给了评估函数的值,优先队列会自己帮我们排序)。

【状态表示】:
直觉上,每个状态用一个N*N的矩阵来表示。
实际上,用一个字符串就可以表示,比如上图的状态1就可以用283104765来表示。每个状态的具体构成就对这个字符串取索引。
【判断状态已经遍历过了】:
用一个dict即字典来判断,dict(key = str, value = 1),如果这个key不在字典里,那么没有被遍历过。如果这个key在字典里且dict[key]==1,那么被遍历过。
字典要求key是一种可hash的对象,当然,字符串肯定是hash的了,所以可以作为key。
【评估函数】:
f(n)=g(n)+h(n)。g(n)代表从起点到当前状态已经造成的花费,而h(n)代表当前状态到终点估计用的花费。
h(n)既然是作为估计用,那么首先得保证两点:
1)直观上,它得估计出当前状态与终点大概相差有多少(但这里只能是大概,如果是精确的,那么就没有意义,因为这样的评估函数肯定很慢,虽说它能求出精确解)
2)它得够快。理由同上。
在二维矩阵中求最短路径时,评估函数的h(n)代表的是当前状态到终点的曼哈顿距离(确实很直观也很快)。
在本问题中,评估函数的h(n)代表的是,当前状态代表的二维矩阵和终点代表的二维矩阵,它们之间有多少个对应元素不一样。即不一样的个数。
下面的是搜索过程:
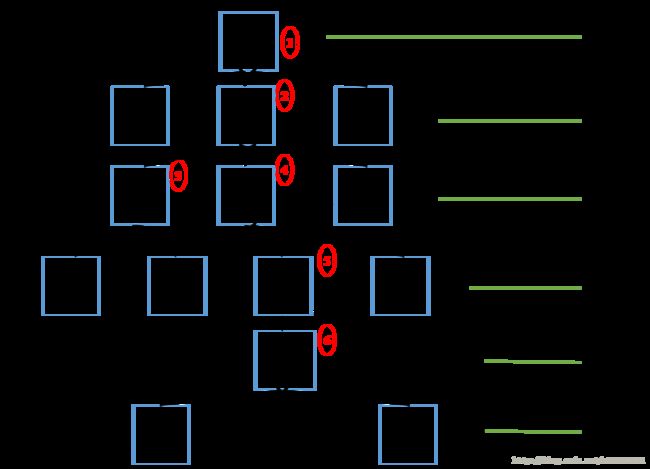
每个等式的等号右边,其左边的是h(n),其右边是g(n)。
八数码问题 代码
from queue import PriorityQueue
class node:
#定义状态类
def __lt__(self,other):
#重载默认的<的函数,加入优先队列时,会被调用
return self.cost < other.cost
def __init__(self,n,s,p):
self.num = n#状态的字符串,str
self.step = s#当前已经走了的步数,int
self.zeroPos = p#0的位置,int(0—N**2-1)
self.cost = 0#评估函数f(n)的值
self.parent = None#父指针,指向上一个状态
self.setCost()
def setCost(self):
#计算评估函数的值
global des
count = 0
for i in range(len(des)):
if self.num[i] != des[i]:
count += 1
self.cost = count + self.step
#左边是h(n),右边是g(n)
def setParent(self,father):
#设置父状态
self.parent = father
def swap(li,first,second):
#li is list
#first and second are index
temp = li[first]
li[first] = li[second]
li[second] = temp
def format_p(s,N):
#格式化打印每个状态,成一个矩阵的样子
for i in range(N):
print(s[i*N:(i+1)*N])
print()
changeId = [
[-1,-1,3,1],[-1,0,4,2],[-1,1,5,-1],
[0,-1,6,4],[1,3,7,5],[2,4,8,-1],
[3,-1,-1,7],[4,6,-1,8],[5,7,-1,-1]
]
#changeId二维数组,行row代表状态里每个元素的序号
#列col代表上左下右四个方向
#changeId的元素代表,状态里每个元素在当前方向是否可以移动
#如果可以移动,给出移动后的元素序号,否则为-1
def bfs(start,zeroPos):
#start is str
#zeroPos is int
global changeId,visit,que,des,N
startNode = node(start,0,zeroPos)
que.put(startNode)#BFS广度遍历之前,要进入第一个状态
while(not que.empty()):
outNode = que.get()
string = outNode.num
if string in visit:
#一个未出过队的状态,可能会重复入队,但队列不提供检测重复功能
#不加此判断,会有重复操作
continue
visit[string] = 1
#出队后,visit字典对应key置1,代表已经被遍历过
strList = [i for i in string]
#字符串属于不可变对象,这里转换成list,方便调用swap函数
pos = outNode.zeroPos
for i in range(4):
#分别判断四个方向
if changeId[pos][i] != -1:#如果这个方向可以移动
swap(strList,pos,changeId[pos][i])#交换两个索引上的元素
join = ''.join(strList)#转换回字符串
if join == des:
#此时找到了终点
print('bingo')
return outNode#返回的是终点前的状态
if join not in visit:#如果没有被访问过
new = node(join,outNode.step+1,changeId[pos][i])#创建新状态
new.setParent(outNode)#设置父状态
que.put(new)#入队
swap(strList,pos,changeId[pos][i])#交换回来,为下一个方向作准备
visit = dict()
que = PriorityQueue()
#N = eval(input())
N = 3
#src = input()
src = '216408753'
#des = input()
des = '123804765'
for i in range(len(src)):
if src[i] == '0':#找到起点的0的位置(0—N**2-1)
break
last = bfs(src,i)
result = [des]#装字符串,用作栈使用,先加入终点
def findroot(last,result):
result.append(last.num)
if last.parent == None:
return
else:
findroot(last.parent,result)
findroot(last,result)
print('从起点到终点')
while(len(result)):
format_p(result.pop(),N)
print('一共走了'+str(last.step+1)+'步')
print('end')
注释我觉得很详细了。
讲讲此代码的优缺点吧:
1)缺点:输入的值N,src,des是写死的(这个是小问题,好改)
2)缺点:changeId是写死的,这里应该根据N来实现
3)优点:if string in visit: continue,这句减少了很多的重复的出队操作。
4)优点:new.setParent(outNode),为每个状态设置父状态,然后可以根据最后一个状态找到之前的状态,一直到起点,然后就可以打印出状态转移的全过程。
5)findroot函数我用的递归实现,嗯,这是个尾递归,可以改成循环的,但我就是想用递归来写。
N数码问题
上面实现了3*3的矩阵,下面推广到N*N的矩阵。
首先changeId需要根据N来实现。
第二点是visit要求key可hash,但这里一个元素可以是两个字符,比如111,它到底是1和11呢还是11和1呢,所以这里就不能再用字符串这种方便的形式了。用元祖就好了,元祖可hash,作为visit的key。
输入:
4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0
5 1 2 4 9 6 3 8 13 15 10 11 14 0 7 12
from queue import PriorityQueue
class node:
def __lt__(self,other):
return self.cost < other.cost
def __init__(self,n,s,p):
self.num = n#str的数组
self.step = s#当前已经走了的步数,int
self.zeroPos = p#0的位置,int
self.cost = 0
self.parent = None#父指针
self.setCost()
def setCost(self):
global des
count = 0
for i in range(len(des)):
if self.num[i] != des[i]:
count += 1
self.cost = count + self.step
def setParent(self,father):
self.parent = father
def swap(li,first,second):
temp = li[first]
li[first] = li[second]
li[second] = temp
def format_p(s,N):
for i in range(N):
print('\t'.join(s[i*N:(i+1)*N]))
print()
def makeChangeId(N):
#根据N实现changeId
li = []
MAX = N**2
for i in range(MAX):
temp = []
row = i//N#行
col = i%N#列
if row is not 0:#上,如果行为0,那么肯定不往上移动了
temp.append(i-N)
else:
temp.append(-1)
if col is not 0:#左
temp.append(i-1)
else:
temp.append(-1)
if row is not N-1:#下
temp.append(i+N)
else:
temp.append(-1)
if col is not N-1:#右
temp.append(i+1)
else:
temp.append(-1)
li.append(temp)
return li
def bfs(start,zeroPos):
#start is str's list
#zeroPos is int
global changeId,visit,que,des,N
#该函数返回最后一个状态即最后一个node
startNode = node(start,0,zeroPos)
que.put(startNode)
while(not que.empty()):
outNode = que.get()
strList = outNode.num#这里是list
strTuple = tuple(strList)#状态表示,这里是tuple
if strTuple in visit:
continue
visit[strTuple] = 1
pos = outNode.zeroPos#零的位置
for i in range(4):
if changeId[pos][i] != -1:
swap(strList,pos,changeId[pos][i])
joinTuple = tuple(strList)
if strList == des:
print('bingo')
swap(strList,pos,changeId[pos][i])
#找到了先交换回去,因为这里strList是状态对象的成员了,直接返回的话,就不会执行
#下面那句swap了,所以这里得加上一句swap
return outNode
if joinTuple not in visit:
new = node(strList.copy(),outNode.step+1,changeId[pos][i])
#注意这里必须使用copy,因为不复制传进去的就只是个引用,会导致所有node的成员都是同一个list
new.setParent(outNode)
que.put(new)
swap(strList,pos,changeId[pos][i])
visit = dict()
que = PriorityQueue()
N = eval(input())
src = input().split()#和之前不同,这里存的都是str的list
des = input().split()
for i in range(len(src)):
if src[i] == '0':
break
changeId = makeChangeId(N)
last = bfs(src,i)
result = [des]#先装des,用作栈使用
def findroot(last,result):
result.append(last.num)
if last.parent == None:
return
else:
findroot(last.parent,result)
findroot(last,result)
print('从起点到终点的状态转移')
while(len(result)):
format_p(result.pop(),N)
print('一共走了'+str(last.step+1)+'步')
print('end')
注释了与之前代码不一样的地方。
运行此测试用例只需要14步。
“优化” 松弛操作
优化很类似于最短路径中的松弛操作。
提前声明:测试证明此版本的优化并没有什么用,但是作为思考,我还是留下此章。PS:不想看的可以跳过!
【参考博客】:
八数码问题的A*算法实现——入门向。其中的大方向都是一样的,但有一点不一样。就是文中提到open和close表,换成本文中的表述来说的话,就是:
open就是优先队列里面的状态,close就是出队过的状态。close里面的状态可能还会再次入队,因为评估函数的结果更低,明显队列中此时会有两个相同的状态,但由于后进来的状态评估值更低,所以就会先执行评估值低的了。
from queue import PriorityQueue
class node:
def __lt__(self,other):
return self.cost < other.cost
def __init__(self,n,s,p):
self.num = n#一维排开的数,str
self.step = s#当前已经走了的步数,int
self.zeroPos = p#0的位置,int
self.cost = 0
self.parent = None#父指针
self.setCost()
def setCost(self):
global des
count = 0
for i in range(len(des)):
if self.num[i] != des[i]:
count += 1
self.cost = count + self.step
def setParent(self,father):
self.parent = father
def swap(li,first,second):
temp = li[first]
li[first] = li[second]
li[second] = temp
def format_p(s,N):
for i in range(N):
print('\t'.join(s[i*N:(i+1)*N]))
print()
def makeChangeId(N):
#根据N实现changeId
li = []
MAX = N**2
for i in range(MAX):
temp = []
row = i//N#行
col = i%N#列
if row is not 0:#上,如果行为0,那么肯定不往上移动了
temp.append(i-N)
else:
temp.append(-1)
if col is not 0:#左
temp.append(i-1)
else:
temp.append(-1)
if row is not N-1:#下
temp.append(i+N)
else:
temp.append(-1)
if col is not N-1:#右
temp.append(i+1)
else:
temp.append(-1)
li.append(temp)
return li
def bfs(start,zeroPos):
#start is str's list
#zeroPos is int
global changeId,visit,que,des,N
#该函数返回最后一个状态即最后一个node
startNode = node(start,0,zeroPos)
que.put(startNode)
while(not que.empty()):
outNode = que.get()
strList = outNode.num#这里是list
strTuple = tuple(strList)#状态表示,这里是tuple
if (strTuple in visit) and (visit[strTuple] <= outNode.cost):
print('cost还是比之前出队的高,那么就continue掉,正常操作')
continue
elif (strTuple in visit) and (visit[strTuple] > outNode.cost):
print('此时出现优化情况,但此句从没有打印过')
visit[strTuple] = outNode.cost#设置对应状态的cost
pos = outNode.zeroPos#零的位置
for i in range(4):
if changeId[pos][i] != -1:
swap(strList,pos,changeId[pos][i])
joinTuple = tuple(strList)
if strList == des:
print('bingo')
swap(strList,pos,changeId[pos][i])#找到了先交换回去,因为这里是倒数第二个状态
return outNode
if joinTuple not in visit:
new = node(strList.copy(),outNode.step+1,changeId[pos][i])
new.setParent(outNode)
que.put(new)
else:#出队过也有可能再次入队,如果cost更低的话
new = node(strList.copy(),outNode.step+1,changeId[pos][i])
if new.cost < visit[joinTuple]:
print('再次入队')
new.setParent(outNode)
que.put(new)
swap(strList,pos,changeId[pos][i])
visit = dict()#要么没有这个状态,要么就是 key=状态:value=cost
que = PriorityQueue()
N = eval(input())
src = input().split()#和之前不同,这里存的都是str的list
des = input().split()
for i in range(len(src)):
if src[i] == '0':
break
changeId = makeChangeId(N)
last = bfs(src,i)
result = [des]
def findroot(last,result):
result.append(last.num)
if last.parent == None:
return
else:
findroot(last.parent,result)
findroot(last,result)
print('从起点到终点的状态转移')
while(len(result)):
format_p(result.pop(),N)
print('一共走了'+str(last.step+1)+'步')
print('end')
讲解:
1)visit字典存状态对应的cost,如果该状态已经被出队过了。
2) 一个状态虽然出队过,但由于第二次重复出现的状态的cost,比出队时的cost更低,这时这个第二次重复出现的状态就会再次入队
3)改动有两点:
if joinTuple not in visit:这个if后面加了else用来判断2)说的情况,但测试多个用例发现,这里的print根本没有打印过,也就是说,一个出队过的状态A,根本不会在这里出现又一个cost更低的状态A,然后让其再次入队。所以说,根本就没有需要优化的操作。猜想这里还是因为优先队列的原因吧,所以不会有这种情况。elif (strTuple in visit) and (visit[strTuple] > outNode.cost):,为了假设可能出现的上述情况,这里设了这么一个判断,但这里的打印也从来没有出现过。这里的意思是,如果一个状态已经出队且新的重复状态比之前出队的旧的重复状态的cost更低的话,就不能直接continue掉,而是继续执行后面的语句,因为出现了更好的重复状态,即cost更小。
4)综上所述,本章的改动以及对其进行的优化实际是没有优化效果的(加了和没加一样)。唯一的情况是:“状态A入队(此时没有一个A出队过),然后又来了一个cost更低的状态A,此时队列里有两个状态A”,换句话说,两个状态A的step应该是一样的,然后再让优先队列去帮我们选择更小cost的状态A出队。
八数码问题有解条件
当你运行某些测试用例,会发现程序一直运行而不出结果,因为此时初始状态到目标状态之间是无法转换到的,即无解的。本章参考了博客八数码问题有解的条件及其推广。
1)首先分析八数码问题的有解条件(3*3矩阵,3是奇数):
一个状态表示成一维的形式,求出除0之外所有数字的逆序数之和,也就是每个数字前面比它大的数字的个数的和,称为这个状态的逆序。若两个状态的逆序奇偶性相同,则可相互到达,否则不可相互到达。 逆序数的思想及代码来自本人博客逆序数问题 使用归并排序。
也就是说,逆序的奇偶将所有的状态分为了两个等价类,同一个等价类中的状态都可相互到达。
简要说明一下:当左右移动空格时,逆序不变。当上下移动空格时,相当于将一个数字向前(或向后)移动两格,跳过的这两个数字要么都比它大(小),逆序可能±2;要么一个较大一个较小,逆序不变。所以可得结论:只要是相互可达的两个状态,它们的逆序奇偶性相同。我想半天只能说明这个结论的必要性,详细的证明请参考后面的附件。
左右移动空格,不改变逆序数,这很好理解。而上下移动空格,分析如下:
| 移动前 | 移动后 |
|---|---|
| 1 2 3 4 5 7 6 8 0 |
1 2 3 4 5 0 6 8 7 |
本来如上矩阵的逆序只有[7,6],当把7移动到下面时,改变了7与6 8之间的顺序,此时逆序就只有[8,7]了。逆序数的个数都是1,所以奇偶性没有变。
2)然后再分析N*N矩阵,N为偶数时的有解条件:
当左右移动空格时,逆序不变。而当上下移动的时候,相当于一个数字跨过了另外三个格子,它的逆序可能±3或±1(这里假设N为4),逆序的奇偶性必然改变。
空格位置所在的行到目标空格所在的行步数为空格的距离(不计左右距离)。
| 状态A | 状态B | 状态C |
|---|---|---|
| 1 2 3 4 5 6 7 8 9 A B C D E F 0 |
1 2 3 4 5 6 7 8 9 A B 0 C D E F |
2 1 3 4 5 6 7 8 9 A B 0 C D E F |
分析上下移动,状态A到状态B虽然二者逆序数相同都为0,但是0位置的行数相差是奇数,所以导致状态A到状态B无解。
如果再将状态B的逆序数的奇偶性改变,比如从B到C,那么就可以从就可以从状态A到状态C。
若(初始状态的逆序数 + 空格距离)的奇偶性==目标状态的逆序数的奇偶性,则可相互到达,否则不可相互到达。
3)总结:
无论N是奇数还是偶数,空格上下移动,相当于跨过N-1个格子。那么逆序的改变可能为一下值±N-1,±N-3,±N-5 …… ±N-2k-1。当N为奇数数时N-1为偶数,逆序改变可能为0;当N为偶数时N-1为奇数,逆序的改变不能为0,只能是奇数,所以每上下移动一次奇偶性必然改变。
from queue import PriorityQueue
class node:
def __lt__(self,other):
return self.cost < other.cost
def __init__(self,n,s,p):
self.num = n#一维排开的数,str
self.step = s#当前已经走了的步数,int
self.zeroPos = p#0的位置,int
self.cost = 0
self.parent = None#父指针
self.setCost()
def setCost(self):
global des
count = 0
for i in range(len(des)):
if self.num[i] != des[i]:
count += 1
self.cost = count + self.step
def setParent(self,father):
self.parent = father
def swap(li,first,second):
temp = li[first]
li[first] = li[second]
li[second] = temp
def format_p(s,N):
for i in range(N):
print('\t'.join(s[i*N:(i+1)*N]))
print()
def makeChangeId(N):
#根据N实现changeId
li = []
MAX = N**2
for i in range(MAX):
temp = []
row = i//N#行
col = i%N#列
if row is not 0:#上,如果行为0,那么肯定不往上移动了
temp.append(i-N)
else:
temp.append(-1)
if col is not 0:#左
temp.append(i-1)
else:
temp.append(-1)
if row is not N-1:#下
temp.append(i+N)
else:
temp.append(-1)
if col is not N-1:#右
temp.append(i+1)
else:
temp.append(-1)
li.append(temp)
return li
def bfs(start,zeroPos):
#start is str's list
#zeroPos is int
global changeId,visit,que,des,N
#该函数返回最后一个状态即最后一个node
startNode = node(start,0,zeroPos)
que.put(startNode)
while(not que.empty()):
outNode = que.get()
strList = outNode.num#这里是list
strTuple = tuple(strList)#状态表示,这里是tuple
if strTuple in visit:
continue
visit[strTuple] = 1
pos = outNode.zeroPos#零的位置
for i in range(4):
if changeId[pos][i] != -1:
swap(strList,pos,changeId[pos][i])
joinTuple = tuple(strList)
if strList == des:
print('bingo')
swap(strList,pos,changeId[pos][i])
#找到了先交换回去,因为这里strList是状态对象的成员了,直接返回的话,就不会执行
#下面那句swap了,所以这里得加上一句swap
return outNode
if joinTuple not in visit:
new = node(strList.copy(),outNode.step+1,changeId[pos][i])
#注意这里必须使用copy,因为不复制传进去的就只是个引用,会导致所有node的成员都是同一个list
new.setParent(outNode)
que.put(new)
swap(strList,pos,changeId[pos][i])
def Inverse_num(arr):#求数组的逆序数
def merge(start,former,latter,end,src,des):
gap = end -start +1
i = start
j = latter
count = 0
for step in range(gap):
if (i<=former) and (j<=end):
if src[i] <= src[j]:
des[start+step] = src[i]
i += 1
else:#j元素比i元素小,那么j肯定也比前子序列中的i后面的元素小
des[start+step] = src[j]
j += 1
count += latter - i#记录下来前子序列i之后元素个数,包括i
elif (i<=former):
des[start+step] = src[i]
i += 1
elif (j<=end):
des[start+step] = src[j]
j += 1
for step in range(gap):
src[start+step] = des[start+step]
return count
def merge_sort(start,end,src,des):
if start < end:
count = 0
mid = (start+end)//2
count += merge_sort(start,mid,src,des)
count += merge_sort(mid+1,end,src,des)
count += merge(start,mid,mid+1,end,src,des)
return count
return 0
def copy_array(arr):
return [None for i in range(len(arr))]
temp = copy_array(arr)
n = len(arr)
num = merge_sort(0,n-1,arr,temp)
return num
visit = dict()
que = PriorityQueue()
N = eval(input())
src = input().split()#存的是str的list
des = input().split()
srcInt = list(map(int,src))#list中元素类型从str到int
srcZeroPos = srcInt.index(0)#src中0一字排开的序号
srcInt.remove(0)#再去掉0
desInt = list(map(int,des))
desZeroPos = desInt.index(0)
desInt.remove(0)
flag = True#代表有解
if N%2 == 1:
if (Inverse_num(srcInt)%2) != (Inverse_num(desInt)%2):
print('初始状态无法转移到目标状态,无解!')
flag = False
else:
ZeroRowDis = abs(srcZeroPos//N - desZeroPos//N)
if ((Inverse_num(srcInt)+ZeroRowDis)%2) != (Inverse_num(desInt)%2):
print('初始状态无法转移到目标状态,无解!')
flag = False
if flag == True:
for i in range(len(src)):
if src[i] == '0':
break
changeId = makeChangeId(N)
last = bfs(src,i)
result = [des]#先装des,用作栈使用
def findroot(last,result):
result.append(last.num)
if last.parent == None:
return
else:
findroot(last.parent,result)
findroot(last,result)
print('从起点到终点的状态转移')
while(len(result)):
format_p(result.pop(),N)
print('一共走了'+str(last.step+1)+'步')
print('end')
无解输入一:
4
1 2 3 4 9 6 7 8 5 0 11 12 13 14 15 10
5 1 2 4 9 6 3 8 13 15 10 11 14 0 7 12
无解输入二:
3
1 2 3 4 5 6 7 8 0
2 1 3 4 5 6 7 8 0