深度学习与计算机视觉(五)神经网络结构与神经元激励函数
五、神经网络结构与神经元激励函数
5.1 神经元激励与连接
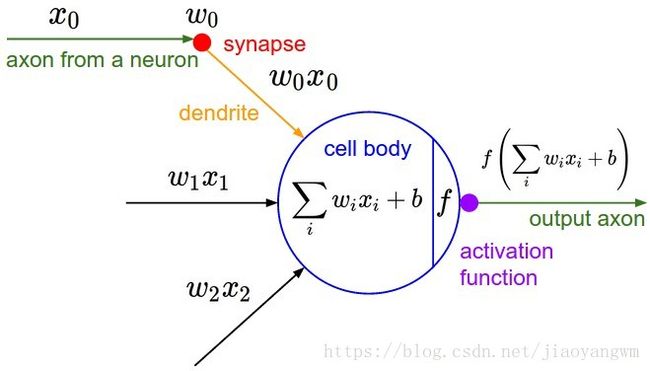
在信号的传导过程中,突触可以控制传导到下一个神经元的信号强弱(数学模型中的权重w ),而这种强弱是可以学习到的。在基本生物模型中,树突传导信号到神经元细胞,然后这些信号被加和在一块儿了,如果加和的结果被神经元感知超过了某种阈值,那么神经元就被激活,同时沿着轴突向下一个神经元传导信号。
在我们简化的数学计算模型中,我们假定有一个『激励函数』来控制加和的结果对神经元的刺激程度,从而控制着是否激活神经元和向后传导信号。比如说,我们在逻辑回归中用到的sigmoid函数就是一种激励函数,因为对于求和的结果输入,sigmoid函数总会输出一个0-1之间的值,我们可以认为这个值表明信号的强度、或者神经元被激活和传导信号的概率。
简单的例子:
class Neuron:
# ...
def forward(inputs):
"""
假定输入和权重都是1维的numpy数组,同时bias是一个数
"""
cell_body_sum = np.sum(inputs * self.weights) + self.bias
firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
return firing_rate1
解释:每个神经元对应输入和权重做内积,加上偏移量bias,然后通过激励函数之后,输出结果。
5.1.1 单个神经元的分类作用
单个神经元的作用,可视作完成一个二分类的分类器(比如Softmax或者SVM分类器)
- 二值softmax分类器
标记σ 为sigmoid映射函数,则 σ(∑iwixi+b) σ ( ∑ i w i x i + b ) 可视作二分类问题中属于某个类的概率 P(yi=1∣xi;w) P ( y i = 1 ∣ x i ; w ) ,我们使用交叉熵损失作为损失函数,得到一组参数W,b就可以帮助我就将空间进行线性分割。如果神经元的预测大于0.5,则会判定属于这个类别。
- 二值SVM分类器
设定max-margin hinge loss作为损失函数,将其训练为一个二值SVM分类器
- 正则化
对于正则化损失函数,其实在神经元的生物特性上都有对应的解释,我们可以将正则化的作用视为信号在神经元传递过程中的逐步淡化 / 衰减,因为正则化的作用在每次迭代的过程中,控制住权重w是幅度,往0上靠拢。
5.1.2 常用激励函数
1)sigmoid函数
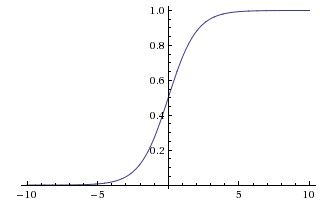
数学形式:
功能:
将实数压缩到0~1之间,数字非常大的时候,结果接近于1,而非常大的负数作为输入,则会得到接近于0的结果。早期的神经网络中,应用的非常多,大家觉得其很好的解释了神经元受到刺激之后是否被激活和后向传递的场景。
缺点:
sigmoid函数在实际的传递过程中,容易饱和和终止梯度传递。
反向传播过程中,依赖于所计算的梯度,在一元函数中也就是斜率,sigmoid函数中,纵坐标接近于0和1的位置(也就是信号的幅值很大),斜率都趋于0了。
反向传播最后用于迭代的梯度是由中间这些梯度结果相乘得到的,因此如果中间的局部梯度值非常小的话,直接会把最终的梯度结果拉进于0。
这种情况下,如果权值初始化的不恰当,且使用sigmoid作为激励函数的话,很可能神经元都饱和,无法学习,使得神经网络无法训练。
sigmoid 函数的输出没有进行0中心化,因为每一层的输出都要作为下一层的输入,而未进行0中心化会直接影响梯度下降。
假设输出的结果全都为正(例如 f=wTx+b f = w T x + b 中所有 x>0 x > 0 ),那么反向传播回传到w上的梯度将要么全部为正,要么全部取负(取决于 f f 的梯度的正负性),这带来的后果是,反向传播得到的梯度用于权值更新的时候,不是平缓的迭代变换,而是类似锯齿状的突变。
2)tanh函数

Tanh函数的图像如上图所示。它会将输入值压缩至-1到1之间,当然,它同样也有sigmoid函数里说到的第一个缺点,在很大或者很小的输入值下,神经元很容易饱和。但是它缓解了第二个缺点,它的输出是0中心化的。所以在实际应用中,tanh激励函数还是比sigmoid要用的多一些的。
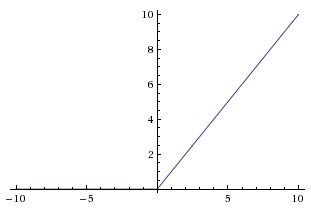
3)ReLU函数
ReLU是修正线性单元(The Rectified Linear Unit)的简称,近些年使用的非常多,图像如上图所示。它对于输入 x x 计算 f(x)=max(0,x) f ( x ) = m a x ( 0 , x ) 。换言之,以0为分界线,左侧都为0,右侧是y=x这条直线。
优点:
缺点:
- 训练过程中很脆弱,也就是如果一个很大的梯度经过ReLU,那权值的更新结果可能是在此之后任何的数据点都没有办法再激活它了,一旦发生,那本应该经过这个ReLU回传的梯度,将永远变为0。 这和参数设置有很大的关系,所以要很小心的设置参数。假设学习率设置的太高,训练的过程中可能有40%的ReLU单元都会失去作用。
4)Leaky ReLU
上面不是提到ReLU单元的弱点了嘛,所以孜孜不倦的ML researcher们,就尝试修复这个问题咯,他们做了这么一件事,在x<0的部分,leaky ReLU不再让y的取值为0了,而是也设定为一个坡度很小(比如斜率0.01)的直线。f(x)因此是一个分段函数,x<0时,f(x)=αx (α 是一个很小的常数),x>0时,f(x)=x 。有一些researcher们说这样一个形式的激励函数帮助他们取得更好的效果,不过似乎并不是每次都比ReLU有优势。
5)Maxout
简单说来,它是ReLU和Leaky ReLU的一个泛化版本。对于输入x,Maxout神经元计算 max(wT1x+b1,wT2x+b2) m a x ( w 1 T x + b 1 , w 2 T x + b 2 ) 。有意思的是,如果你仔细观察,你会发现ReLU和Leaky ReLU都是它的一个特殊形式(比如ReLU,你只需要把 w1,b1 w 1 , b 1 设为0)。因此Maxout神经元继承了ReLU单元的优点,同时又没有『一不小心就挂了』的担忧。如果要说缺点的话,你也看到了,相比之于ReLU,因为有2次线性映射运算,因此计算量也double了。
5.2 神经网络的结构
5.2.1 层间级联结构
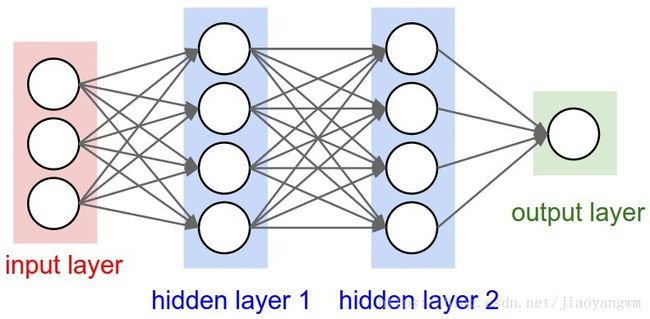
神经网络的结构其实之前也提过,是一种单向的层级连接结构,每一层可能有多个神经元。再形象一点说,就是每一层的输出将会作为下一层的输入数据,一般情况下,单层内的这些神经元之间是没有连接的。最常见的一种神经网络结构就是全连接层级神经网络,也就是相邻两层之间,每个神经元和每个神经元都是相连的,单层内的神经元之间是没有关联的。下面是两个全连接层级神经网的示意图:
5.2.2 前向传播计算
神经网络组织成上述结构,很重要的一个原因是层间的计算可以很方便的表示为矩阵之间的运算,就是一直重复权值和输入做内积后经过激励函数变换的过程。
# 3层神经网络的前向运算:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # 简单起见,我们还是用sigmoid作为激励函数吧
x = np.random.randn(3, 1) # 随机化一个输入
h1 = f(np.dot(W1, x) + b1) # 计算第一层的输出
h2 = f(np.dot(W2, h1) + b2) # 计算第二层的输出
out = np.dot(W3, h2) + b3 # 最终结果 (1x1)上述代码中,W1,W2,W3,b1,b2,b3都是待学习的神经网络参数。注意到我们这里所有的运算都是向量化/矩阵化之后的,x不再是一个数,而是包含训练集中一个batch的输入,这样并行运算会加快计算的速度,仔细看代码,最后一层是没有经过激励函数,直接输出的。
5.2.3 神经网络的表达力和模型大小
其实,包含一个隐藏层(2层神经网络)的神经网络已经具备大家期待的能力,即只要隐藏层的神经元个数足够,我们总能用它(2层神经网络)去逼近任何连续函数(即输入到输出的映射关系)。详细的内容可以参加Approximation by Superpositions of Sigmoidal Function或者Michael Nielsen的介绍。我们之前的博文手把手入门神经网络系列(1)_从初等数学的角度初探神经网络也有提到。
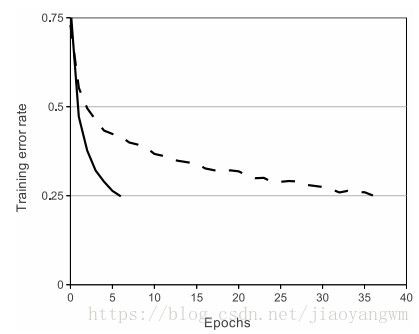
问题是,如果单隐藏层的神经网络已经可以近似逼近任意的连续值函数,那么为什么我们还要用那么多层呢?很可惜的是,即使数学上我们可以用2层神经网近似几乎所有函数,但在实际的工程实践中,却是没啥大作用的。多隐藏层的神经网络比单隐藏层的神经网络工程效果好很多,即使从数学上看,表达能力应该是一致的。
不过还得说一句的是,通常情况下,我们工程中发现,3层神经网络效果优于2层神经网络,但是如果把层数再不断增加(4,5,6层),对最后结果的帮助就没有那么大的跳变了。不过在卷积神经网上还是不一样的,深层的网络结构对于它的准确率有很大的帮助,直观理解的方式是,图像是一种深层的结构化数据,因此深层的卷积神经网络能够更准确地把这些层级信息表达出来。
5.2.4 层数和参数设定的影响
一个很现实的问题,我们拿到一个实际问题的时候,怎么知道应该如何去搭建一个网络结构,可以最好的解决这个问题?
直观理解,当我们加大层数以及每一层的神经元个数的时候,我们的神经网络变大了,也就是神经网络的空间表达能力变的更丰富了。
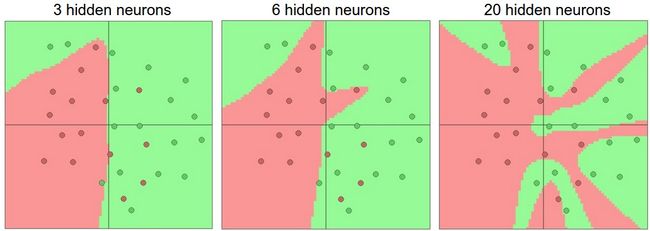
例如,我们现在要处理一个二分类问题,输入是二维的,我们训练三个不同神经元个数的单隐层神经网络,它们的平面表达能力对比画出来如下:
分析:更多的神经元可以让网络有更好的拟合复杂空间函数的能力,但是任何事物都有双面性,拟合过好带来的问题是很容易带来过拟合现象,会将离群点和噪声点都学习下来,使得在未知的测试集上没有泛化能力,分类效果极差。
分析:经过上图分析,可能会觉得对于不是很复杂的问题,用更少的层数和神经元的话会不容易过拟合,但这个想法是错误的,永远不要使用减少层数和神经元的方式来缓解过拟合,这会极大的影响神经网络的表达能力。
如何缓解过拟合:正则化
不要使用少层少神经元的简单神经网络的另外一个原因是,其实我们用梯度下降等方法,在这种简单神经网上,更难训练得到合适的参数结果。对,你会和我说,简单神经网络的损失函数有更少的局部最低点,应该更好收敛。是的,确实是的,更好收敛,但是很快收敛到的这些个局部最低点,通常都是全局很差的。相反,大的神经网络,确实损失函数有更多的局部最低点,但是这些局部最低点,相对于上面的局部最低点,在实际中效果却更好一些。对于非凸的函数,我们很难从数学上给出100%精准的性质证明,大家要是感兴趣的话,可以参考论文The Loss Surfaces of Multilayer Networks。
如果你愿意做多次实验,会发现,训练小的神经网络,最后的损失函数收敛到的最小值变动非常大。这意味着,如果你运气够好,那你maybe能找到一组相对较为合适的参数,但大多数情况下,你得到的参数只是在一个不太好的局部最低点上的。相反,大的神经网络,依旧不能保证收敛到最小的全局最低点,但是众多的局部最低点,都有相差不太大的效果,这意味着你不需要借助”运气”也能找到一个近似较优的参数组。
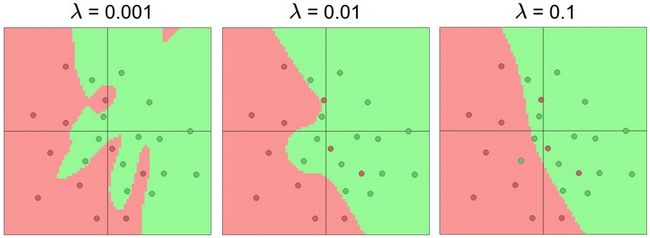
最后,我们提一下正则化,我们说了要用正则化来控制过拟合问题。正则话的参数是λ ,它的大小体现我们对参数搜索空间的限制,设置小的话,参数可变动范围大,同时更可能过拟合,设置太大的话,对参数的抑制作用太强,以至于不太能很好地表征类别分布了。下图是我们在上个问题中,使用不同大小的正则化参数λ得到的平面分割结果。
5.3 正则化
L2正则化:
这个我们之前就提到过,非常常见。实现起来也很简单,我们在损失函数里,加入对每个参数的惩罚度。也就是说,对于每个权重w ,我们在损失函数里加入一项 12λw2 1 2 λ w 2 ,其中λ是我们可调整的正则化强度。顺便说一句,这里在前面加上1/2的原因是,求导/梯度的时候,刚好变成 λw λ w 而不是 2λw 2 λ w 。L2正则化理解起来也很简单,它对于特别大的权重有很高的惩罚度,以求让权重的分配均匀一些,而不是集中在某一小部分的维度上。我们再想想,加入L2正则化项,其实意味着,在梯度下降参数更新的时候,每个权重以W += -lambda*W的程度被拉向0。
L1正则化:
这也是一种很常见的正则化形式。在L1正则化中,我们对于每个权重w 的惩罚项为 λ|w| λ | w | 。有时候,你甚至可以看到大神们混着L1和L2正则化用,也就是说加入惩罚项 λ1∣w∣+λ2w2 λ 1 ∣ w ∣ + λ 2 w 2 。
L1正则化有其独特的特性,它会让模型训练过程中,权重特征向量逐渐地稀疏化,这意味着到最后,我们只留下了对结果影响最大的一部分权重,而其他不相关的输入(例如『噪声』)因为得不到权重被抑制。所以通常L2正则化后的特征向量是一组很分散的小值,而L1正则化只留下影响较大的权重。在实际应用中,如果你不是特别要求只保留部分特征,那么L2正则化通常能得到比L1正则化更好的效果
最大范数约束:
另外一种正则化叫做最大范数约束,它直接限制了一个上行的权重边界,然后约束每个神经元上的权重都要满足这个约束。实际应用中是这样实现的,我们不添加任何的惩罚项,就按照正常的损失函数计算,只不过在得到每个神经元的权重向量 w⃗ w ⃗ 之后约束它满足 ∥w⃗ ∥2<c ∥ w ⃗ ∥ 2 < c 。有些人提到这种正则化方式帮助他们提高最后的模型效果。
另外,这种正则化方式倒是有一点很吸引人:在神经网络训练学习率设定很高的时候,它也能很好地约束住权重更新变化,不至于直接挂掉。
Dropout:
这个是我们实际神经网络训练中,用的非常多的一种正则化手段,同时也相当有效。Srivastava等人的论文Dropout: A Simple Way to Prevent Neural Networks from Overfitting最早提到用dropout这种方式作为正则化手段。
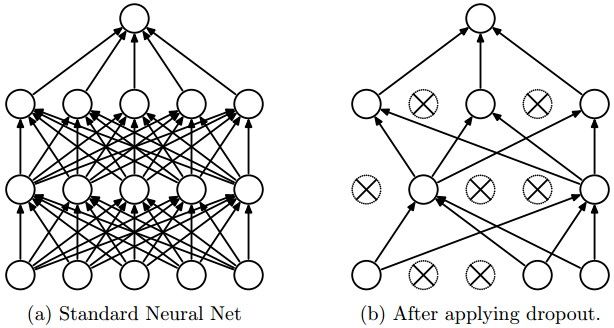
一句话概括它,就是:在训练过程中,我们对每个神经元,都以概率p保持它是激活状态,1-p的概率直接关闭它。
解析:在训练过程中,对全体神经元,以概率p做了一个采样,只有选出的神经元要进行参数更新,所以最后就从左图的全连接变为右图的Dropout后的神经元连接图了,测试阶段,我们不用dropout,而是直接从概率的角度,对权重配以一个概率值。
bias项的正则化:
其实我们在之前的博客中提到过,我们大部分时候并不对偏移量项做正则化,因为它们也没有和数据直接有乘法等交互,也就自然不会影响到最后结果中某个数据维度的作用。不过如果你愿意对它做正则化,倒也不会影响最后结果,毕竟总共有那么多权重项,才那么些bias项,所以一般也不会影响结果。
实际应用中:我们最常见到的是,在全部的交叉验证集上使用L2正则化,同时我们在每一层之后用dropout,很常见的dropout概率为p=0.5,你也可以通过交叉验证去调整这个值。
5.4 损失函数
训练的关键之一:损失函数
损失函数:评价预测值和真实结果之间的吻合程度
损失函数原理:实际上是计算出了每个样本上的loss,再求平均之后的一个形式 L=1N∑iLi L = 1 N ∑ i L i ,其中N是训练样本数。
5.4.1 分类问题
5.4.2 回归问题
5.5 总结
- 在很多神经网络的问题中,我们都建议对数据特征做预处理,去均值,然后归一化到[-1,1]之间。
- 从一个标准差为 2/n−−−√ 2 / n 的高斯分布中初始化权重,其中n为输入的个数。
- 使用L2正则化(或者最大范数约束)和dropout来减少神经网络的过拟合。
- 对于分类问题,我们最常见的损失函数依旧是SVM hinge loss和Softmax互熵损失。