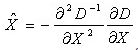SIFT算法特征描述子构建---关键点定位原理及代码

0.引言

sift针对局部特征进行特征提取，在尺度空间寻找极值点，提取位置，尺度，旋转不变量，生成特征描述子。

总共分四个步骤：

• 尺度金字塔生成
• 关键点/极值点提取
• 生成梯度直方图
• 特征描述子构建

step2 关键点/极值点提取

2.1 关键点位置初步探查

生成DOG金字塔后，要找到DOG空间中的局部极值点。第一步首先根据DOG空间内，各点响应大小检测和筛选极值点。
选择策略如下：

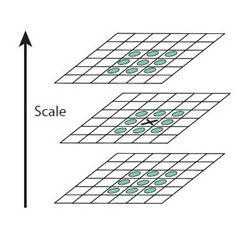
中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。
由于要在相邻尺度进行比较，高斯差分金子塔S+2层，头尾两层无法计算，因此，定义的INTERVALS层数就是指检测极值点的层数。

bool isExtremum(int x,int y,const vector& dog_pyr,int index)//x为列，y为行
{
    pixel_t* data = (pixel_t*)dog_pyr[index].data;          //当前层数据的指针
    pixel_t val = *(data + dog_pyr[index].cols*y + x);      //当前点像素
    //检查是否为极大值
    if (val>0)
    {
        for (int i = -1; i < 2; i++)
        {
            int col_cur= dog_pyr[index+i].cols;             //当前层列数
            for (int j = -1; j < 2; j++)
            {
                for (int k = -1; k < 2; k++)
                {
                    if (val<*((pixel_t*)dog_pyr[index+i].data+col_cur*(y+j)+x+k))
                    {
                        return false;
                    }
                }
            }
        }
    }//极大值
     //检查是否为极小值
    else
    {
        for (int i = -1; i < 2; i++)
        {
            int col_cur = dog_pyr[index + i].cols;              //当前层列数
            for (int j = -1; j < 2; j++)
            {
                for (int k = -1; k < 2; k++)
                {
                    if (val > *((pixel_t*)dog_pyr[index + i].data + col_cur*(y + j) + x + k))
                    {
                        return false;
                    }
                }
            }
        }
    }//极小值
    return true;
}

当然这样产生离散空间的极值点并不全都是稳定的特征点，因为某些极值点响应较弱（对比度低），同时DOG算子会产生较强的边缘响应。为了解决这两个问题，需要对极值点进行插值和筛选。

2.2 关键点插值定位修正和边缘响应去除

2.2.1位置修正及去除低响应

插值需要将离散的图像表达式，表达为连续的函数。以下通过拟合三维二次函数（二阶的泰勒展开式）来精确确定关键点的位置和尺度。

其中是位置和尺度三个变量的向量。

二次函数对称轴就是极值点偏移量：

此处，为了求此公式，需要提前定义好计算逆矩阵，二阶偏导，一阶偏导 的函数。

/*************************************************************************************************************************
*模块说明：
*       求偏差量预备工作 【1】返回第index层的金字塔在y行x列的值
*功能说明：
*       PryAt（）---At：在该层y行x列的值
**************************************************************************************************************************/
pixel_t PyrAt(const vector<Mat>& pyr, int index, int x, int y)
{
    pixel_t *data = (pixel_t*)pyr[index].data;
    pixel_t val = *(data + y*pyr[index].cols + x);
    return val;
}
#define At(index, x, y) (PyrAt(dog_pyr, (index), (x), (y)))  
/*************************************************************************************************************************
*模块说明：
*       求偏差量预备工作，【2】对x,y,sigma的一阶偏导存入dx[3]
*功能说明：
*       使用节点的一阶中心差分近似导数，  取最小h=1时，最精确
*       f'(xi)=(f(xi+h)-f(xi-h))/2h
*       f'(yi)=(f(yi+h)-f(yi-h))/2h
*       f'(si)=(f(si+h)-f(si-h))/2h
**************************************************************************************************************************/
void DerivativeOf3D(int x,int y,const vector<Mat>& dog_pyr,int index,double *dx)
{
    dx[0] = (double)(At(index, x + 1, y) - At(index, x - 1, y)) / 2.0;
    dx[1] = (double)(At(index, x, y + 1) - At(index, x, y - 1)) / 2.0;
    dx[2] = (double)(At(index + 1, x, y) - At(index - 1, x, y)) / 2.0;
}
/*************************************************************************************************************************
*模块说明：
*       求偏差量预备工作，【3】对x,y,sigma的二阶偏导存入Hat(3*3),对称阵
*   |   Dxx Dxy Dxs     |
*   |   Dyx Dxy Dys     |
*   |   Dsx Dsy Dss     |
*功能说明：
*       使用节点的一阶中心差分近似导数，  取最小h=1时，最精确
*       Dxx=f''(xi)=(f(xi+h)+f(xi-h)-2*f(xi))/h^2
*       Dxy=f''(yi)=(f(yi+h)+f(yi-h)-2*f(yi))/h^2
*       Dss=f''(si)=(f(si+h)+f(si-h)-2*f(si)))/h^2
*
*       Dyx=Dxy=f''(xi)(yi)=(f(xi+h,yi+h)+f(xi-h,yi-h)-f(xi+h,yi-h)-f(xi-h,yi+h))/4*h
**************************************************************************************************************************/
#define Hat(i,j) (*(H+3*(i)+(j)))
void Hessian3D(int x, int y, const vector<Mat>& dog_pyr, int index, double*H)
{
    Hat(0, 0) = At(index, x + 1, y) + At(index, x - 1, y) - 2 * At(index, x, y);//Dxx
    Hat(1, 1) = At(index, x, y + 1) + At(index, x, y - 1) - 2 * At(index, x, y);//Dyy
    Hat(1, 1) = At(index + 1, x, y) + At(index - 1, x, y) - 2 * At(index, x, y);//Dss
    Hat(1, 0) = Hat(0, 1) = (At(index, x + 1, y + 1) + At(index, x - 1, y - 1) - At(index, x + 1, y - 1) - At(index, x - 1, y + 1)) / 4.0;//Dxy
    Hat(2, 0) = Hat(0, 2) = (At(index + 1, x + 1, y) + At(index - 1, x - 1, y) - At(index - 1, x + 1, y) - At(index + 1, x - 1, y)) / 4.0;//Dxs
    Hat(2, 1) = Hat(1, 2) = (At(index + 1, x, y + 1) + At(index - 1, x, y - 1) - At(index + 1, x, y - 1) - At(index - 1, x, y + 1)) / 4.0;//Dsy
}
/*************************************************************************************************************************
*模块说明：
*       三阶矩阵求逆
**************************************************************************************************************************/
#define HIat(i, j) (*(H_inve+3*(i)+j))
bool Inverse3D(const double *H,double *H_inve)
{
    //行列式
    double A =Hat(0, 0)*Hat(1, 1)*Hat(2, 2)
            + Hat(0, 1)*Hat(1, 2)*Hat(2, 0)
            + Hat(0, 2)*Hat(1, 0)*Hat(2, 1)
            - Hat(0, 0)*Hat(1, 2)*Hat(2, 1)
            - Hat(0, 1)*Hat(1, 0)*Hat(2, 2)
            - Hat(0, 2)*Hat(1, 1)*Hat(2, 0);
    if (fabs(A)<1e-10)  return false;
    HIat(0, 0) = Hat(1, 1) * Hat(2, 2) - Hat(2, 1)*Hat(1, 2);
    HIat(0, 1) = -(Hat(0, 1) * Hat(2, 2) - Hat(2, 1) * Hat(0, 2));
    HIat(0, 2) = Hat(0, 1) * Hat(1, 2) - Hat(0, 2)*Hat(1, 1);
    //伴随矩阵第二行
    HIat(1, 0) = Hat(1, 2) * Hat(2, 0) - Hat(2, 2)*Hat(1, 0);
    HIat(1, 1) = -(Hat(0, 2) * Hat(2, 0) - Hat(0, 0) * Hat(2, 2));
    HIat(1, 2) = Hat(0, 2) * Hat(1, 0) - Hat(0, 0)*Hat(1, 2);
    //伴随矩阵第三行
    HIat(2, 0) = Hat(1, 0) * Hat(2, 1) - Hat(1, 1)*Hat(2, 0);
    HIat(2, 1) = -(Hat(0, 0) * Hat(2, 1) - Hat(0, 1) * Hat(2, 0));
    HIat(2, 2) = Hat(0, 0) * Hat(1, 1) - Hat(0, 1)*Hat(1, 0);
    for (int i = 0; i < 9; i++)
    {
        *(H_inve + i) /= A;
    }
    return true;
}

这样就可以计算偏差量了。

/*************************************************************************************************************************
*模块说明：计算x,y,sigma 的偏差量x^、y^、sigma^
*       
*模块内容       1.x^=-(Dxx*dx+Dxy*dy+Dxs*ds)  DOG函数拟合函数的逆矩阵的二阶和拟合函数一阶（为什么这个公式）
**************************************************************************************************************************/
void GetoffsetX(int x, int y, const vector<Mat>& dog_pyr, int index, double* offset_x)
{
    //求一阶偏导
    double dx[3];
    DerivativeOf3D(x, y, dog_pyr, index, dx);
    //求二阶偏导
    double H[9], H_inve[9] = {0};
    Hessian3D(x, y, dog_pyr, index, H);
    if (Inverse3D(H, H_inve))
    {
        for (int i = 0; i < 3; i++)
        {
            offset_x[i] = 0.0;
            for (int j = 0; j < 3; j++)
            {
                offset_x[i] += H_inve[i * 3 + j] * dx[j];
            }
            offset_x[i]=-offset_x[i];
        }
    }
    else
        cout << "无海森逆矩阵" << endl;

得到偏移量后，首先判断x,y,sigma任意维度的偏移量是否超过0.5，其次论文中拟合的迭代次数为5次。另外，对比度小于0.03的 极值点也要去除。
极值点处的值计算公式为：

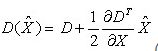
//2.D（x^）=D+0.5*D'^T(x)*x^=D()+0.5*(Dx*offset[0] +Dy* offset[1]+Ds* offset[2])
//计算D（x^）
double GetFabsDx(int x,int y,const vector& dog_pyr,int index,const double *offset_x)
{
    double dx[3];
    DerivativeOf3D(x, y, dog_pyr, index, dx);
    double term = 0.0;
    for (int i = 0; i < 3; i++)
    {
        term += dx[i] * offset_x[i];
    }
    pixel_t val = At(index, x, y);
    return fabs(val+0.5*term);
}

整个筛选并保存关键点如下：

/*************************************************************************************************************************
*模块说明：
*       模块四的第二步:修正极值点，删除不稳定的点
*功能说明:
*       1--根据高斯差分函数产生的极值点并不全都是稳定的特征点，因为某些极值点的响应较弱，而且DOG算子会产生较强的边缘响应
*       2--以上方法检测到的极值点是离散空间的极值点，下面通过拟合三维二次函数来精确定位关键点的位置和尺度，同时去除对比度
*          低和不稳定的边缘响应点(因为DOG算子会产生较强的边缘响应)，以增强匹配的稳定性、提高抗噪声的能力。
*       3--修正极值点，删除不稳定点，|D(x)| < 0.03 Lowe 2004
**************************************************************************************************************************/
Keypoint* InterpolationExtremum(int x ,int y, const vector& dog_pyr, int index, int octave, int interval, double dxthreshold)
{
    double offset_x[3] = {0};
    const Mat &mat = dog_pyr[index];
    int idx = index;
    //int intvl=interval;
    int i = 0;
    for (; i < MAX_INTERPOLATION_STEPS; i++)
    {
        //求取偏移量
        GetoffsetX(x, y, dog_pyr, idx, offset_x); 
        //如果offset_x 的任一维度大于0.5，插值中心已经偏移到它的邻近点上
        if (fabs(offset_x[0]) < 0.5 && fabs(offset_x[1]) < 0.5 && fabs(offset_x[2]) < 0.5)  break;  
        ////将找到的极值点对应成像素（整数），用周围点代替
        x += cvRound(offset_x[0]);
        y += cvRound(offset_x[1]);
        interval += cvRound(offset_x[2]);
        idx = octave* (INTERVALS+2)+ interval;
        //超出图像层或者图像边界的范围
        if (interval<1||interval>INTERVALS||x>mat.cols-2||x<2|| y>mat.rows - 2 || y<2)  return NULL;

    }
    //超出所设定的迭代次数
    if (i>=MAX_INTERPOLATION_STEPS) return NULL;
    //|D(x^)| < 0.03取经验值 
    if (GetFabsDx(x, y, dog_pyr, idx, offset_x) < dxthreshold / INTERVALS)  return NULL;
    //则属于关键点
    Keypoint* keypoint = new Keypoint;
    keypoint->x = x;
    keypoint->y = y;
    //keypoint->val=At()

    keypoint->offset_x = offset_x[0];
    keypoint->offset_y = offset_x[1];
    keypoint->offset_interval = offset_x[2];

    keypoint->octave = octave;
    keypoint->interval = interval;

    keypoint->dx = (x + offset_x[0])*pow(2.0, octave); //缩放成原图像大小
    keypoint->dy = (y + offset_x[1])*pow(2.0, octave);
    return keypoint;
}

2.2.2边缘响应去除

为了剔除边缘响应点，需要让下比值小于一定的阈值
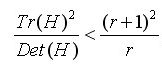)成立时将关键点保留，反之剔除。
其中，在Lowe的文章中，取r＝10。在Lowe的文章中，取r＝10。

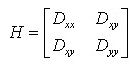
bool passEdgeResponse(int x,int y,vector& dog_pyr,int index,double r)
{
    //求二阶偏导
    double H[9];
    Hessian3D(x, y, dog_pyr, index, H);
    double Tr_h = H[0] + H[4];//Dxx+Dyy
    double Det_h = H[0] * H[4] - H[1] * H[1];//Dxx * Dyy - Dxy * Dxy
    if (Det_h<=0)   return false;
    if (Tr_h*Tr_h / Det_h < (r + 1)*(r + 1) / r)    return true;
    return false;
}

2.2.3 关键点生成保存

通过调用上述过程函数，将关键点位置尺度信息保存。
关键点数据结构：

struct Keypoint
{
    int octave;                 //【1】关键点所在组
    int interval;               //【2】关键点所在层

    double offset_interval;     //【3】调整后层的增量（是3/2吗,怎么是double?）

    int x, y;                   //【4】x,y坐标,根据octave和interval可取的层内图像（是指所在组层？）
    double scale;               //【5】空间尺度坐标scale = sigma0*pow(2.0, o+s/S)  

    double dx, dy;              //【6】特征点坐标，该坐标被缩放成原图像大小
    double offset_x, offset_y;

    //============================================================  
    //特征描述子
    //============================================================  
    double octave_scale;        //【1】offset_i
    double ori;                 //【2】方向
    double descriptor[FEATURE_ELEMENT_LENTH];//【3】特征描述子
    int descr_length;
    double val;                 //【4】极值
};

保存函数：

void DetectionLocalExtrema(vector& dog_pyr,vector& extrema,int intervals)
{
    int octaves = (int)dog_pyr.size() / (intervals+2);      //DOG组数
    double thresh=0.5*DXTHRESHHOLD/intervals;               
    for (int  o = 0; o < octaves; o++)
    {
        for (int i = 1; i < intervals+1; i++)
        {
            int index = o*(intervals + 2) + i;              //当前层的索引序号
            pixel_t *data =(pixel_t*) dog_pyr[index].data;  //当前层数据首地址
            //对每层进行提取特征点
            for (int y = IMG_BORDER; y < dog_pyr[index].rows-IMG_BORDER; y++)
            {
                for (int x = IMG_BORDER; x < dog_pyr[index].cols-IMG_BORDER; x++)
                {
                    pixel_t val = *(data + y*dog_pyr[index].cols + x);
                    //当大于阈值，并且时是26个中极值点时
                    if (fabs(val)>thresh&&isExtremum(x,y,dog_pyr,index))
                    {
                        Keypoint *extrum = InterpolationExtremum(x, y, dog_pyr, index, o, i);
                        if (extrum)
                        {
                            if (passEdgeResponse(extrum->x,extrum->y,dog_pyr,index))
                            {

                                extrum->val = At(index,extrum->x,extrum->y);
                                extrema.push_back(*extrum);
                            }
                            delete extrum;
                        }
                    }
                }
            }
        }
    }
}

2.2.4 尺度

void CalculateScale(vector& features, double sigma, int intervals)
{
    double intvl = 0.0;
    for (int i = 0; i < features.size(); i++)
    {
        intvl = features[i].interval + features[i].offset_interval;
        features[i].scale = sigma * pow(2.0, features[i].octave + intvl / intervals);
        features[i].octave_scale = sigma * pow(2.0, intvl / intervals);
    }

}
//对扩大的图像特征缩放，对应到原图大小（非-1层）  
void HalfFeatures(vector& features)
{
    for (int i = 0; i < features.size(); i++)
    {
        features[i].dx /= 2;
        features[i].dy /= 2;
        features[i].scale /= 2;
    }
}