caioj1212:【计算几何】判断线段相交(快速排斥判断与跨立实验)
首先,欢迎大家来访问我老师的OJ:小白菜OJ
你是新入门OI的小白吗?
你正在苦于网上的资料不足吗?
你正在因各种blog写得不清不楚、艰涩难懂、千篇一律、满篇术语像LB一样而烦恼吗?
欢迎来到小白菜OJ!
这里有最易懂的视频讲解、基于HustOJ和阿里云的稳定、先进OJ
并且——完全免费!
小白菜OJ——信息学竞赛在线自学系统(caioj.cn)
以上为广告内容
说实话我觉得这道题才是真正的计算几何题
相对于这道题正方形那道真是太水了
正文
题面传送门(需要注册账号)
大意:
你按顺序丢了一堆线段到平面上,问你能直接拿起几根(不用搬走其他的线段)
前置知识
不是前置知识的东西:
本文使用结构体储存点和线段
所有的坐标都在笛卡儿坐标系中定义
说人话就是我用的是平面直角坐标系
端点结构体:
struct point
{
double x,y;//横、纵坐标
};
线段结构体:
struct segment
{
point l,r;//懒得打编号了,就直接记作左右端点(虽然可能不科学)
}
叉积
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。
——百度百科
向量的坑以后再补
叉积是什么?
我也想知道
叉积就是两个向量形成的平行四边形的面积大小。
C A → \overrightarrow{CA} CA与 C B → \overrightarrow{CB} CB的叉积记为 C A → × C B → \overrightarrow{CA}\times\overrightarrow{CB} CA×CB
就像这样:
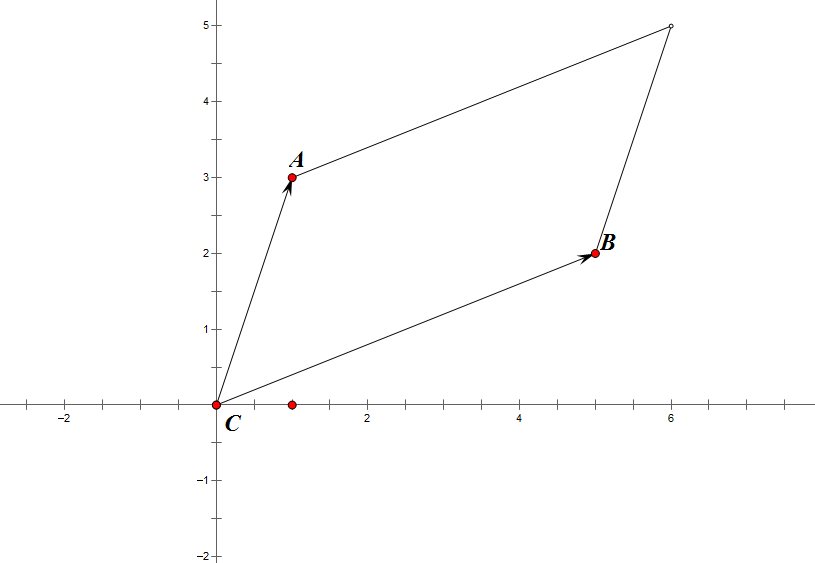
图中平行四边形的面积就是 C A → × C B → \overrightarrow{CA}\times\overrightarrow{CB} CA×CB(的大小)
(其实叉积是也一个向量,但我们在这里只讨论它的大小了啦!)
计算方法:
我们可以由三个点的坐标(图中的 A , B , C A,B,C A,B,C)计算出两个向量的叉积
推导:
平行四边形的面积可以由 2 S △ A B C 2S_{\triangle ABC} 2S△ABC得到
作辅助矩形 C D F E CDFE CDFE:
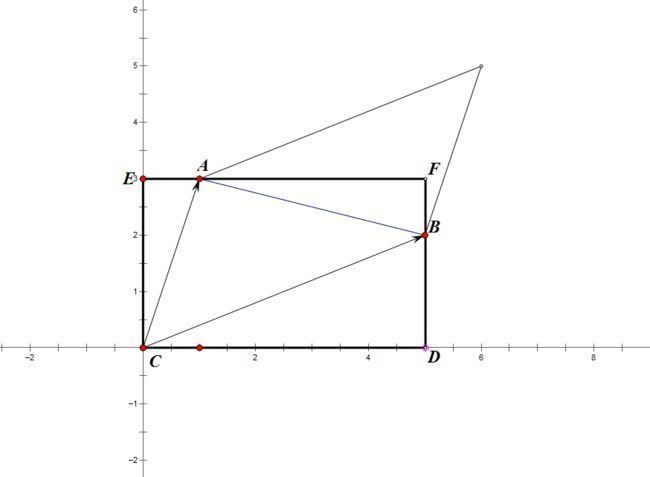
易得:
S △ A B C = S 矩 形 C D F E − S △ A C E − S △ B C D − S △ A B F S_{\triangle ABC}=S_{矩形CDFE}-S_{\triangle ACE}-S_{\triangle BCD}-S_{\triangle ABF} S△ABC=S矩形CDFE−S△ACE−S△BCD−S△ABF
= x B ∗ y A − 1 2 ∗ x A ∗ y A − 1 2 ∗ x B ∗ y B − 1 2 ∗ ( x B − x A ) ∗ ( y A − y B ) =x_B*y_A-\frac12*x_A*y_A-\frac12*x_B*y_B-\frac12*(x_B-x_A)*(y_A-y_B) =xB∗yA−21∗xA∗yA−21∗xB∗yB−21∗(xB−xA)∗(yA−yB)
= x B ∗ y A − 1 2 ∗ x A ∗ y A − 1 2 ∗ x B ∗ y B − 1 2 ∗ x B ∗ y A + 1 2 ∗ x B ∗ y B + 1 2 ∗ x A ∗ y A − 1 2 ∗ x A ∗ y B =x_B*y_A-\frac12*x_A*y_A-\frac12*x_B*y_B-\frac12*x_B*y_A+\frac12*x_B*y_B+\frac12*x_A*y_A-\frac12*x_A*y_B =xB∗yA−21∗xA∗yA−21∗xB∗yB−21∗xB∗yA+21∗xB∗yB+21∗xA∗yA−21∗xA∗yB
= 1 2 ∗ x B ∗ y A − 1 2 ∗ x A ∗ y B =\frac12*x_B*y_A-\frac12*x_A*y_B =21∗xB∗yA−21∗xA∗yB
暴力果然是有用的
所以 C A → × C B → \overrightarrow {CA}\times\overrightarrow {CB} CA×CB就可以表示为:
( x B − x C ) ( y A − y C ) − ( x A − x C ) ( y B − y C ) (x_B-x_C)(y_A-y_C)-(x_A-x_C)(y_B-y_C) (xB−xC)(yA−yC)−(xA−xC)(yB−yC)
说了这么多,叉积有什么用呢?
好吧我们在这里只是用了一个性质:
如果记 C C C为原点的话
那么如果是这样的一个情况:
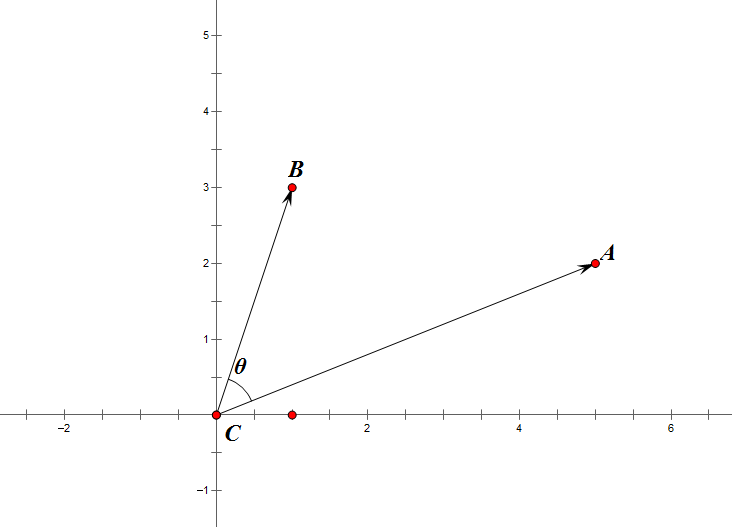
我们会发现, C A → × C B → \overrightarrow{CA}\times\overrightarrow{CB} CA×CB是小于零的!
经过人类几千年以来的观察, 叉积总是在 C A → \overrightarrow{CA} CA位于 C B → \overrightarrow{CB} CB的顺时针方向时小于零,在 C A → \overrightarrow{CA} CA位于 C B → \overrightarrow{CB} CB所在直线上时等于零,在 C A → \overrightarrow{CA} CA位于 C B → \overrightarrow{CB} CB的顺时针方向时
因此,叉积的正负性可以用于判断从 A ⃗ \vec A A到 B ⃗ \vec B B的旋转方向。
真正的正文:
我们来看看两条相交的线段
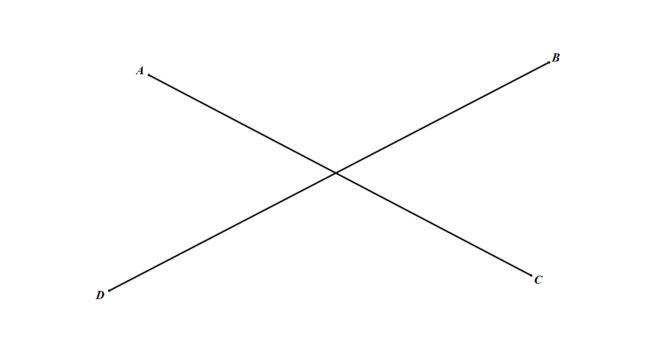
有没有发现相对于 A A A,与它处于同一条线段的另一点 C C C与其它两点 B , D B,D B,D的关系?
好像 A C → \overrightarrow{AC} AC总是被夹在 A B → \overrightarrow{AB} AB和 A D → \overrightarrow{AD} AD中间呢!
仔细看一下好像对于每一个点都是酱紫的诶!
那我们就可以以 A A A做基准点,判断 B , D B,D B,D是不是在 C C C的两边(也就是 A B → × A C → \overrightarrow{AB}\times\overrightarrow{AC} AB×AC与 A D → × A C → \overrightarrow{AD}\times\overrightarrow{AC} AD×AC不同号)就好啦!
等等!
还没好呢!
要是这样呢?
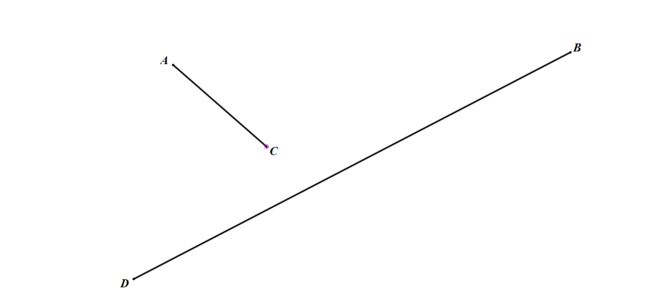

emm……那就再用B做基准点判一次咯……
所以代码就出来了:
bool intersect(line a,line b)
{
#define A a.l
#define B b.l
#define C a.r
#define D b.r
//这几行的意思就是用ABCD四个点表示两条线段的四个端点
if(cp(C,B,A)*cp(C,D,A)<0&&cp(D,A,B)*cp(D,C,B)<0)return 1;
return 0;
#undef A
#undef B
#undef C
#undef D
//这是取消上面的快捷表示,防止以后要用到ABCD
}
且慢!
如果这样呢?
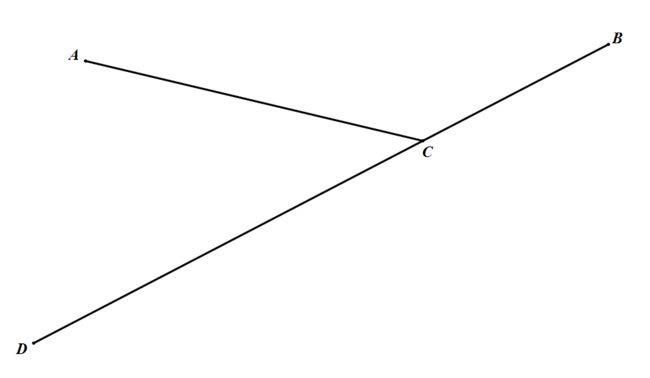
这样的话 B C → × B D → \overrightarrow{BC}\times\overrightarrow{BD} BC×BD就是0了啊!
那要不直接把 < < <改成 ≤ \le ≤?
嘿嘿嘿~~~
直接上图:
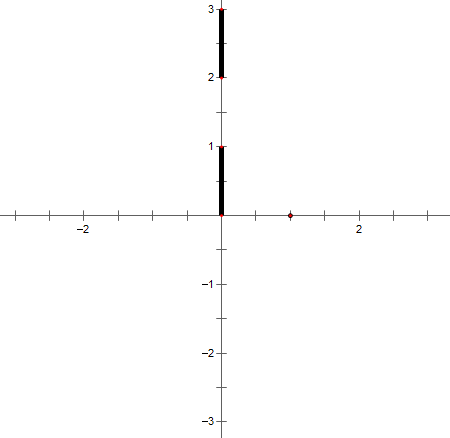
这种情况下会错判
所以!
我们只能暴力判断了!
我们就加入一个东西:
这个东西叫做快速排斥判断。
它的工作原理如下:
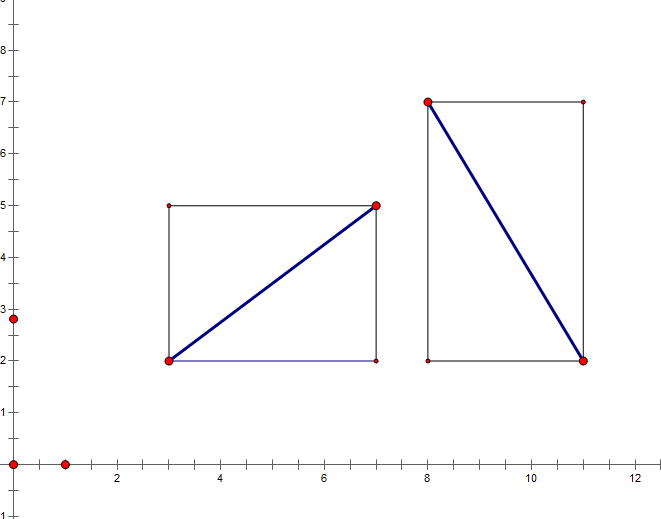
我们用两个矩形框住两条线段
然后判断两个矩形是否有重叠部分
没有的话两条线段就肯定不会相交啊!
这时候我们就把它排除掉。
这个代码也不难:
int amaxx=max(a.l.x,a.r.x),amaxy=max(a.l.y,a.r.y),bmaxx=max(b.l.x,b.r.x),bmaxy=max(b.l.y,b.r.y);
int aminx=min(a.l.x,a.r.x),aminy=min(a.l.y,a.r.y),bminx=min(b.l.x,b.r.x),bminy=min(b.l.y,b.r.y);
if(amaxx<bminx||bmaxx<aminx||amaxy<bminy||bmaxy<aminy)return 0;
最终代码:
#include历时两天,终于写完~~