【Python】Conway生命游戏学习

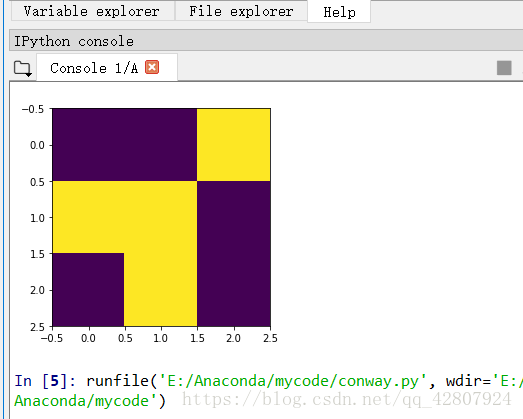
先尝试以下代码，如果成功就可以继续吧

import numpy as np #数组
import matplotlib.pyplot as plt #生成动画
import matplotlib.animation as animation #更新模拟

x = np.array([[0,0,255],[255,255,0],[0,255,0]])#三维数组
plt.imshow(x, interpolation='nearest')#nearest输出尖锐边缘
plt.show()#将矩形输出为图像

最后代码：源码：https://github.com/electronut/pp

"""
conway.py 
A simple Python/matplotlib implementation of Conway's Game of Life.
Author: Mahesh Venkitachalam
"""

import sys, argparse
import numpy as np
import matplotlib.pyplot as plt 
import matplotlib.animation as animation

ON = 255
OFF = 0
vals = [ON, OFF]

def randomGrid(N):
    """returns a grid of NxN random values"""
    return np.random.choice(vals, N*N, p=[0.2, 0.8]).reshape(N, N)

def addGlider(i, j, grid):
    """adds a glider with top left cell at (i, j)"""
    glider = np.array([[0,    0, 255], 
                       [255,  0, 255], 
                       [0,  255, 255]])
    grid[i:i+3, j:j+3] = glider

def addGosperGliderGun(i, j, grid):
    """adds a Gosper Glider Gun with top left cell at (i, j)"""
    gun = np.zeros(11*38).reshape(11, 38)

    gun[5][1] = gun[5][2] = 255
    gun[6][1] = gun[6][2] = 255

    gun[3][13] = gun[3][14] = 255
    gun[4][12] = gun[4][16] = 255
    gun[5][11] = gun[5][17] = 255
    gun[6][11] = gun[6][15] = gun[6][17] = gun[6][18] = 255
    gun[7][11] = gun[7][17] = 255
    gun[8][12] = gun[8][16] = 255
    gun[9][13] = gun[9][14] = 255

    gun[1][25] = 255
    gun[2][23] = gun[2][25] = 255
    gun[3][21] = gun[3][22] = 255
    gun[4][21] = gun[4][22] = 255
    gun[5][21] = gun[5][22] = 255
    gun[6][23] = gun[6][25] = 255
    gun[7][25] = 255

    gun[3][35] = gun[3][36] = 255
    gun[4][35] = gun[4][36] = 255

    grid[i:i+11, j:j+38] = gun

def update(frameNum, img, grid, N):
    # copy grid since we require 8 neighbors for calculation
    # and we go line by line 
    newGrid = grid.copy()
    for i in range(N):
        for j in range(N):
            # compute 8-neghbor sum
            # using toroidal boundary conditions - x and y wrap around 
            # so that the simulaton takes place on a toroidal surface.
            total = int((grid[i, (j-1)%N] + grid[i, (j+1)%N] + 
                         grid[(i-1)%N, j] + grid[(i+1)%N, j] + 
                         grid[(i-1)%N, (j-1)%N] + grid[(i-1)%N, (j+1)%N] + 
                         grid[(i+1)%N, (j-1)%N] + grid[(i+1)%N, (j+1)%N])/255)
            # apply Conway's rules
            if grid[i, j]  == ON:
                if (total < 2) or (total > 3):
                    newGrid[i, j] = OFF
            else:
                if total == 3:
                    newGrid[i, j] = ON
    # update data
    img.set_data(newGrid)
    grid[:] = newGrid[:]
    return img,

#main() function
def main():
    # Command line args are in sys.argv[1], sys.argv[2] ..
    # sys.argv[0] is the script name itself and can be ignored
    # parse arguments
    parser = argparse.ArgumentParser(description="Runs Conway's Game of Life simulation.")
  # add arguments
    parser.add_argument('--grid-size', dest='N', required=False)
    parser.add_argument('--mov-file', dest='movfile', required=False)
    parser.add_argument('--interval', dest='interval', required=False)
    parser.add_argument('--glider', action='store_true', required=False)
    parser.add_argument('--gosper', action='store_true', required=False)
    args = parser.parse_args()
    
    # set grid size
    N = 100
    if args.N and int(args.N) > 8:
        N = int(args.N)
        
    # set animation update interval
    updateInterval = 50
    if args.interval:
        updateInterval = int(args.interval)

    # declare grid
    grid = np.array([])
    # check if "glider" demo flag is specified
    if args.glider:
        grid = np.zeros(N*N).reshape(N, N)
        addGlider(1, 1, grid)
    elif args.gosper:
        grid = np.zeros(N*N).reshape(N, N)
        addGosperGliderGun(10, 10, grid)
    else:
        # populate grid with random on/off - more off than on
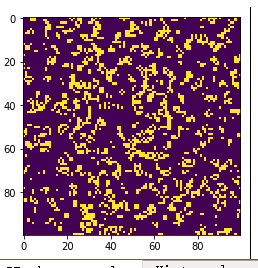
        grid = randomGrid(N)

    # set up animation
    fig, ax = plt.subplots()
    img = ax.imshow(grid, interpolation='nearest')
    ani = animation.FuncAnimation(fig, update, fargs=(img, grid, N, ),
                                  frames = 10,
                                  interval=updateInterval,
                                  save_count=50)

    # # of frames? 
    # set output file
    if args.movfile:
        ani.save(args.movfile, fps=30, extra_args=['-vcodec', 'libx264'])

    plt.show()

#call main
if __name__ == '__main__':
    main()