题目链接：点击查看
题目大意：n 个机器人在数轴上赛跑，给出每个机器人的起点和加速度，初始速度都为 0 ，问有多少个机器人在赛跑的过程中可以成为最前面的一个
题目分析：又是被zx学长秒掉的一道题，感谢zx学长的耐心讲解
首先根据高中物理知识，根据已知条件，可以得到位移与时间的方程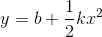 
，y 代表位移，x 代表时间，b 代表初始位置，k 代表加速度
因为都是抛物线，求交点非常的麻烦，因为我们只需要求交点的相对位置，所以可以将方程转换为位移与时间的平方的方程：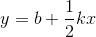
，这样并不会影响交点的相对位置，同时将每一个位移曲线都转换为一条直线表示了
那么如何将机器人成为最前面的一个体现出来呢？将 n 条直线对应到平面直角坐标系中，将 x 轴从 [ 0 , inf ) 划分为无数个点，对于每个 x 而言，对应位置最上面的那条直线所代表的机器人，就是在 x 时刻最领先的机器人，所以我们只需要统计有多少条直线成为过最上面的直线就好了
按照斜率排序，就可以发现相邻的三条直线会出现下面两种情况：
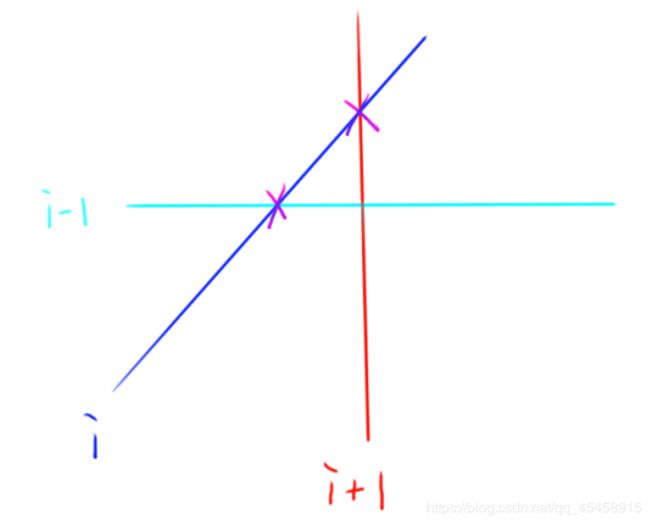
我们将直线 i - 1 与直线 i 的交点记为 ( x1 , y1 ) ，将直线 i 与直线 i + 1 的交点记为 ( x2 , y2 ) ，发现当 x1 < x2 时，直线 i 所代表的机器人才有可能在最上面，而当 x1 >= x2 时，直线 i 完全被直线 i - 1 和直线 i + 1 所挡住，也就无法在最上面了
到此为止，我们就可以利用单调栈来实现上述模拟了，栈内维护的是都可以在最上面的直线，对于新遍历到的直线 i ，因为我们已经按照斜率递增了，显然单调栈内所有初始位置 b 小于当前直线的直线都是不符合条件的，如下图所示：
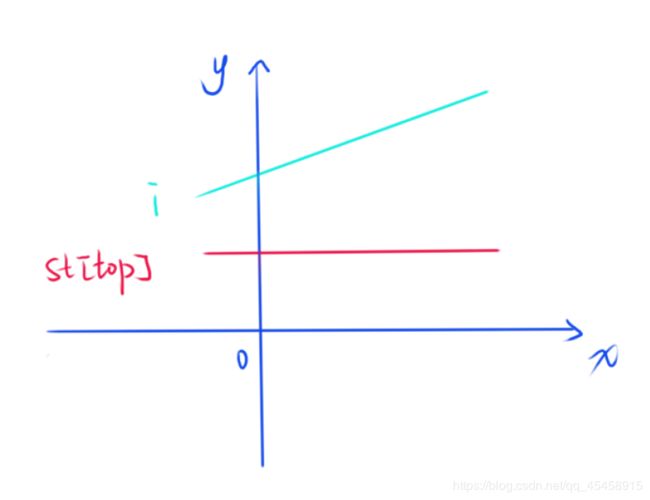
显然在上图中，st [ top ] 所代表的直线完全被第 i 条直线所覆盖
还有就是对于栈中的元素，将 st[ top - 1 ] , st[ top ] 和 i 这三条直线分别对应上文中的 i - 1 , i , i + 1 三条直线来比较交点的位置亦可以判断合理性
最后有个坑点，就是如果有两个机器人，起点和加速度都是相同的话，那么这两个机器人是不会对答案提供贡献的，这个可以用 map 判断一下
代码：
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
