【hd水题】hdoj2056 Rectangles

 

Rectangles

 

 

 

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 14378    Accepted Submission(s): 4643

 

 

 

Problem Description

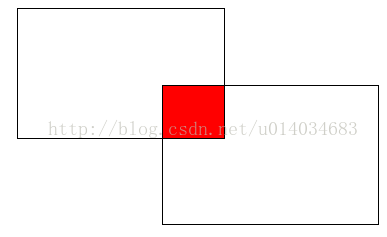
Given two rectangles and the coordinates of two points on the diagonals of each rectangle,you have to calculate the area of the intersected part of two rectangles. its sides are parallel to OX and OY .

 

 

Input

Input The first line of input is 8 positive numbers which indicate the coordinates of four points that must be on each diagonal.The 8 numbers are x1,y1,x2,y2,x3,y3,x4,y4.That means the two points on the first rectangle are(x1,y1),(x2,y2);the other two points on the second rectangle are (x3,y3),(x4,y4).

 

 

Output

Output For each case output the area of their intersected part in a single line.accurate up to 2 decimal places.

 

 

Sample Input

1.00 1.00 3.00 3.00 2.00 2.00 4.00 4.00 5.00 5.00 13.00 13.00 4.00 4.00 12.50 12.50

 

 

Sample Output

1.00 56.25

 

 

 题意: 给出2个矩形各其中一条对角线,求这2个矩形的重合面积

 

分析:由于不确定输入的对角线是什么方向的,所以排列给出的坐标，使得矩形的对角线都是↗的;

 

接着分析矩形是否有碰撞

假设2个矩形的左下和右上 分别为 (x1,y1),(x2,y2) 和 (x3,y3),(x4,y4)

则且仅当 (x4>x1&&y4>y1&&x3

即: 矩形B的右上点>矩形A的左下点&&矩形B的左下点<矩形A的右上点，成立,2个矩形碰撞。

排列四个坐标(x,y)使得：x1

不难求出 宽=x3-x2;
                高=y3-y2；

面积S=宽*高；

代码如下：

#include
int main()
{double x[5],y[5],t,x1,x2,y1,y2;
while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x[1],&y[1],&x[2],&y[2],&x[3],&y[3],&x[4],&y[4])!=EOF)
    {if(x[1]>x[2]) {t=x[1];x[1]=x[2];x[2]=t;}
     if(y[1]>y[2]) {t=y[1];y[1]=y[2];y[2]=t;}
     if(x[3]>x[4]) {t=x[3];x[3]=x[4];x[4]=t;}
     if(y[3]>y[4]) {t=y[3];y[3]=y[4];y[4]=t;}
     x1=x[1]>x[3]?x[1]:x[3];
     x2=x[2]      y1=y[1]>y[3]?y[1]:y[3];
     y2=y[2]      printf("%.2lf\n",x1>x2||y1>y2?0:(x2-x1)*(y2-y1));      
    }
return 0;
}