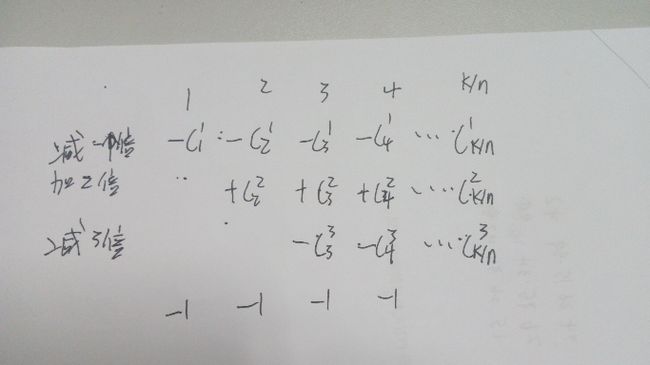hdu多校第八场 hdu6397 Character Encoding 容斥+组合数学

题目连接：Character Encoding

题意：

题解:如果没限制的话，总方案数是就是c(k+m-1，m-1),可以用隔板法的思想，然后就是容斥了，我们还要减去超过n的情况，

如果假设有一个超过n的这样的方案数是c(m,1)*c(k+m-1-n,m-1)但是这样会减去c(2,1)倍的有两个超过n的方案书（既减去c(n,i)倍的有i个超过n的方案数);多减就要加上。

然后加上至少2个超过n的方案数c（m,2）*c(k+m-1-2*n,m-1),这样有就会多加了，然后我们可以发现奇数减偶数加的容斥方法。我下面推了几个小的可以看一下。

#include
using namespace std;
const int mod=998244353;
int n,m,k;
const int N=1e5+5;
int inv[N*2],invf[2*N],f[2*N];
void init(){
    inv[1] =  1;
    f[0] =  invf[0] = 1;
    for(int i = 2;i < 2*N;i ++){
        inv[i] = (mod-mod/i)*1LL*inv[mod%i]%mod;
    }
    for(int i =1;i < 2*N;i ++){
        f[i] = 1ll*f[i-1]*i%mod;
    }
    for(int i = 1;i < 2*N;i ++){
        invf[i] = invf[i-1]*1LL*inv[i]%mod;
    }
}
int c(int x,int y)
{
    if(x< 0 || y > x||y<0) return 0;
    return 1LL*f[x]*invf[y]%mod*invf[x-y]%mod;
}
int main()
{
    int T;
    init();
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d %d %d",&n,&m,&k);
        int ans=0;
        for(int i=0;i<=k/n;i++)
        {
            if(i%2)
            {
                ans-=(1ll*c(m,i)*c(k+m-1-n*i,m-1)%mod);
                if(ans<0)ans+=mod;
            }
            else
            {
                 ans+=(1ll*c(m,i)*c(k+m-1-n*i,m-1)%mod);
                if(ans>=mod)ans-=mod;
            }
        }
        printf("%d\n",ans);
    }
}

 

转载于:https://www.cnblogs.com/lhclqslove/p/9488404.html